11.Использование принципа суперпозиции для линейных многомерных систем .

Для линейных многомерных систем

1.38

справедлив принцип суперпозиции: эффект (изменение состояния системы), вызванный воздействием на систему нескольких внешних воздействий равен сумме эффектов от каждого из таких воздействий в отдельности. В силу линейности уравнения выходов этот же принцип справедлив и для выходного сигнала.

Закон изменения вектора состояний системы представляют в виде суммы свободного и вынужденного движения системы:

Точно также выходной сигнал представляют суммой сигналов, соответствующих свободному и вынужденному движениям системы:

Под свободным движением подразумевается движение системы при ненулевых начальных условиях и отсутствующем (нулевом) входном воздействии

При нулевых начальных условиях свободное движение отсутствует:

Под вынужденным движением системы и соответствующим выходным сигналом подразумевается реакция системы на ненулевое внешнее воздействие при нулевых начальных условиях:

Таким образом, свободное и вынужденное движение системы определяется решением однородных уравнений состояния при ненулевых начальных условиях и неоднородных уравнений состояния при нулевых начальных условиях.

Для нестационарных многомерных линейных систем, которые описываются уравнениями (1.38), законы изменения во времени вектора состояний и вектора выходного сигнала определяются следующими формулами:

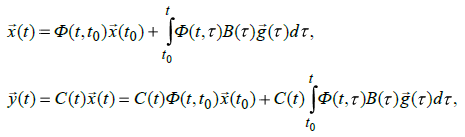
где Ф- переходная матрица, которую называют также матрицей Коши. В решении (1.43) первые слагаемые соответствуют свободному движению системы, вторые – вынужденному.

12. Алгоритм решения задачи анализа выходных процессов в многомерных системах

Алгоритм решения задачи анализа выходных процессов рассмотрим на примере стационарной системы управления

с начальными условиями

и алгебраическими уравнениями выходов

Для анализа выходных процессов необходимо осуществить два шага:

1) найти переходную матрицу. Для этого можно использовать метод (назовем его первым способом решения), основанный на определении фундаментальной матрицы, метод, основанный на применении теоремы разложения Сильвестра, и метод, основанный применении теоремы Кэли-Гамильтона.

2) По известной переходной матрице и приведенным ранее формулам найти законы изменения состояния выходного сигнала.

Рассмотрим алгоритм поиска переходной матрицы

основанный на предварительном определении фундаментальной матрицы .

Этот алгоритм включает следующие действия.

1. Необходимо найти корни характеристического уравнения

где Е — единичная матрица.

1. Для каждой компоненты вектора состояний записывают общее решение однородной системы в виде:

На этом этапе произвольные постоянные для каждой компоненты вектора

состояний считаются различными. При этом используются известные

правила записи общего решения в зависимости от вида корней

характеристического уравнения, которые мы уже обсуждали.

2) Полученные выражения подставляются в однородные уравнения системы. Для каждой компоненты вектора состояний x(t) записать общее решение.

3) Неизвестные коэффициенты при одинаковых функциях независимой переменной t приравниваются между собой.

Последующее решение полученной системы уравнений позволяет выразить часть неизвестных постоянных через другие, так что неизвестными остаются только n констант. При этом зачастую оказывается достаточно рассмотреть первые n-1 уравнение.

4) Записывается общее решение, зависящее от этих n постоянных, что позволяет выписать фундаментальную матрицу , а затем и переходную

.