8. Анализ выходных процессов в линейных системах управления, описываемых дифференциальными уравнениями

Задачи анализа линейных систем подразделяют на следующие виды:

1) основная задача анализа – это анализ выходных процессов;

2) анализ устойчивости;

3) анализ чувствительности;

4) анализ управляемости;

5) анализ наблюдаемости;

Для анализа выходных процессов в стационарных и нестационарных линейных системах управления при тех или иных внешних воздействиях, необходимо найти решение дифференциального уравнения. Прежде чем рассмотреть алгоритм поиска решений, необходимо отметить, что, проанализировав выходные процессы в моделируемой системе при единичном ступенчатом внешнем воздействии, можно определить основные показатели качества системы.

К основным показателям, которые характеризуют переходные процессы в системе управления, относятся следующие.

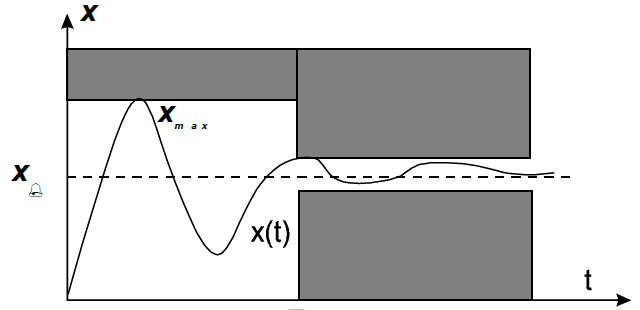
При проектировании систем управления считается, что система удовлетворяет требованиям по качеству, если все перечисленные показатели качества не превышают заранее заданных значений.

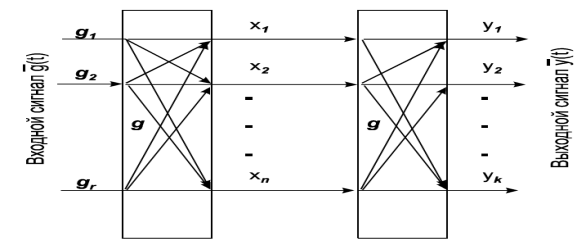
9. Виды многомерных систем

Основы математического моделирования многомерных систем управления рассмотрим, следуя работе. В отличие от одномерных систем, в многомерных системах не по одному входу и выходу, а имеется r входов и k выходов. Поэтому математическая модель системы управления характеризуется тем, что входные, промежуточные и выходные сигналы описывают векторными функциями скалярного аргумента – времени, связи между которыми описываются дифференциальными уравнениями первого порядка.

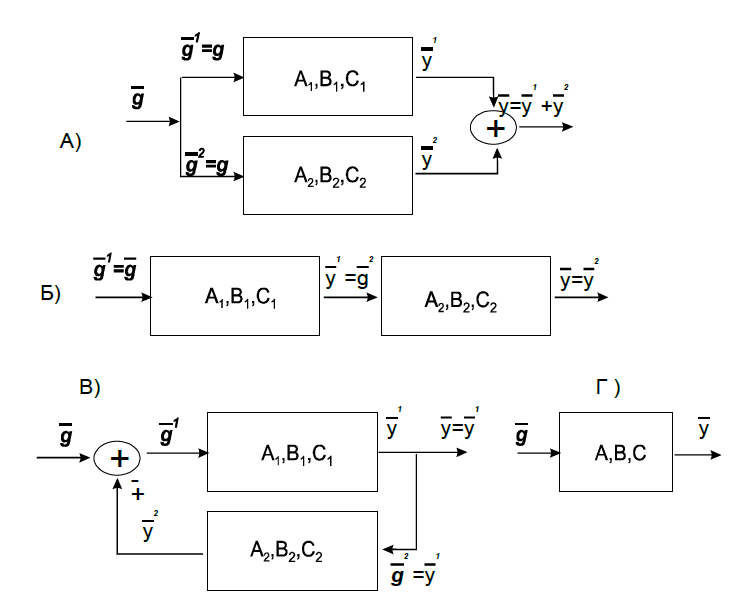
10. Описание соединений многомерных систем (матричные уравнения соединений)

Если математическая модель многомерной системы управления

записана в виде уравнений

то она полностью характеризуется

тремя матрицами A(t) , B(t) , C(t) . Также как и в случае одномерных систем,

две многомерные системы могут образовать параллельное и

последовательное соединение, а также соединение с обратной связью. Эти

типы соединений показаны на рис. 1.14.

Пусть обе системы, которые образуют то или иное соединение, описываются

следующими матричными уравнениями:

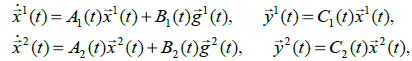
где х¹,g¹,y¹- векторы состояния, входной сигнал и вектор выходных сигналов первой системы (размерность r₁ n₁ k₁ соответственно), х²,g²,y²- векторы состояния, входной сигнал и вектор выходных) сигналов второй системы (размерности r₂ n₂ k₂ ), A(t), B(t), C(t)матрицы - соответствующие матрицы уравнений. Здесь верхний индекс вектора означает номер вектора, а нижние индексы, как и ранее, будем использовать для обозначения номера компоненты вектора. Нижний индекс у матриц обозначает номер матрицы.

При параллельном соединении входной сигнал (вектор) поступает одновременно на оба элемента, а выходной сигнал является результатом суммирования выходных сигналов (тоже векторов) элементов.

Рис1. Параллельное (а) и последовательное (б) соединение многомерных систем, соединение с обратной связью (в), схема эквивалентной системы (г).