20. Построение оптимальных планов экспериментов.
Для построения теории планирования эксперимента требуется более
строгое определение.
Дискретным или точечным планом эксперимента
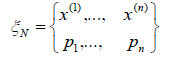
называют
вероятностную меру, сосредоточенную в
точках
весами
где
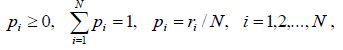
Непрерывным планом эксперимента называется план вида
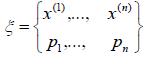
где
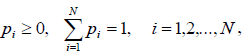
Если на множестве непрерывных планов удается найти
оптимальный
план,
то для применения этих результатов в
конкретных
экспериментах
его «округляют» до дискретного плана
.
Каковы же
критерии оптимальности, которые используются в теории планирования
эксперимента?
Чтобы ответить на этот вопрос, вернемся к определению линейной
модели
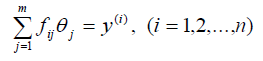
и запишем выражение для информационной матрицы планируемых
экспериментов следующего вида:
Относительно информационной матрицы принимается
существенно важное допущение, что для всех рассматриваемых планов
определитель
Смысл этой величины для
планируемого,
активного,
эксперимента, простой.
- эта величина означает вероятность
(для дискретного плана - относительную
частоту повторений) экспериментов в
одной и той же точке
которая
необходима для
обеспечения оптимальности плана. Понятно, что в выражении
информационной
матрицы реализованных
экспериментов,
эта величина была равна единице для
каждой конкретной экспериментальной
точки
Для планируемого оптимального эксперимента
эта величина, вообще говоря,
должна быть найдена исходя из условий оптимальности.
Таким образом, чтобы построить оптимальный план эксперимента для
модели необходимо выбрать критерий оптимальности плана вида
и решить соответствующую задачу оптимизации. Это достаточно сложная
задача, но для некоторых частных видов моделей эта задача решена и можно
воспользоваться уже имеющимися результатами.