4.2. Перевірка значущості коефіцієнта кореляції

Коефіцієнт кореляції, як вибіркова характеристика, перевіряєть­ся на значущість за допомогою t-критерію Ст’юдента. Фактичне зна­чення t-статистики обчислюється за формулою

(13)

і порівнюється з табличним значенням t-розподілу з n–m–1 ступе­нями свободи та при заданому рівні значущості a/2 (такий рівень зу­мовлений тим, що критична область складається з двох проміжків).

Якщо абсолютна величина експериментального значення t-статистики перевищує табличне, тобто |t_експ|>t_табл, можна зробити висновок, що коефіцієнт кореляції достовірний (зна­чущий), а зв'язок між залежною змінною та всіма незалежними фак­торами суттєвий.

4.3. Оцінка статистичної значущості параметрів моделі

Окрім загальних показників адекватності моделі існують також оцінки, що дають змогу встановити якість окремих частин рівняння, зокрема одного чи кількох коефіцієнтів регресії.

Як і в попередніх випадках, рішення відносно якості коефіцієнтів приймають на основі відповідних статистичних критеріїв.

Статистичну значущість кожного параметра моделі можна пере­вірити за допомогою t-критерію. При цьому нульова гіпотеза має вигляд

Н₀ : _j = 0,

альтернативна

Н_А : _j ≠ 0.

Експериментальне значення t-статистики для кожного параметра моделі обчислюється за формулою

(14)

де С_jj – діагональний елемент матриці (Х′Х)^–1 ;

– стандартна похибка оцінки параметра моделі:

(15)

Експериментальне значення t_j-критерію порівнюється з таблич­ним значенням t_табл з n–m–1 ступенями свободи при заданому рівні значущості a/2 (критична область розбивається на два фрагмен­ти, межі яких задаються квантилем a/2). Якщо значення t-статистики потрапляє до критичної області (за абсолютним значенням пере­вищує t_табл), приймається альтернативна гіпотеза про значущість відповідного параметра. Інакше робиться висновок про статистичну незначущість параметра _j, а це означає, що відповідна незалежна змінна не впливає суттєво на змінювання залежної змінної.

5. Прогнозування за лінійною моделлю

Якщо побудована модель адекватна за F-критерієм, то її застосо­вують для прогнозування залежної змінної. Про прогнозування за моделлю говорять тоді, коли в часових рядах прогнозний період настає пізніше, ніж базовий. Якщо регресія побудо­вана за просторовими даними, прогноз стосується тих елементів гене­ральної сукупності, що перебувають за межами застосованої вибірки.

Припустимо, що ми побудували модель та оцінили параметри методом найменших квадратів. На підставі побудованої моделі можна знайти прогнозні значення матриці залежних змінних Y_пр, які відповідають очікуваним значенням матриці незалежних змінних X_пр.

Прогноз на перспективу буває двох видів: точковий та інтервальний.

Незміщена оцінка точкового прогнозу може розглядатися як точкова оцінка математичного сподівання прогнозного значення Y_пр

(16)

а також як індивідуальне значення Y_пр для матриці незалежних змінних Х_пр, що лежать за межами базового періоду .

Дисперсія похибки прогнозу дорівнює

(17)

де – дисперсия залишків u, яка розраховується за формулою (2.9);

var(B) – дисперсійно-коваріаційна матриця, яка записується у вигляді:

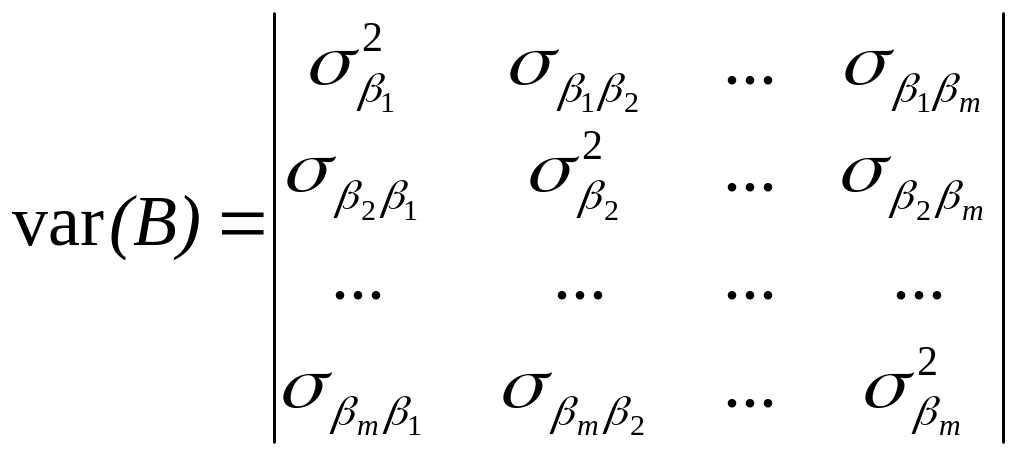(18)

Елементи на головній діагоналі матриці та за її межами розраховуються за формулами:

(19)

(20)

де с_jj, c_jk – елементи матриці похибок (ХХ)^–1.

Тоді дисперсія прогнозу буде:

(21)

Середньоквадратична (стандартна) похибка прогнозу:

(22)

Довірчий інтервал для прогнозних значень:

(23)

де t_– табличне значення t-критерія Ст'юдента з (n–m–1) ступенями вільності  – рівень значимості.

Для використання t-критерія Ст'юдента необхідно обрати бажаний рівень значимості  (0,05 або 0,01) та число ступенів вільності (n–m–1).

Інтервальній прогноз математичного сподівання М(Y_пр) буде в межах:

(24)

Визначення інтервального прогнозу індивідуального значення Y_пр базується на знаходженні середньоквадратичної помилки прогнозу:

(25)

Тоді інтервальний прогноз індивідуального значення буде відповідати такому довірчому інтервалу:

(26)