Практичнее заняття 1

Методи побудови математичних моделей економічних систем по статистичним даним.

1. Прості лінійні регресійні моделі

2. Оцінка тісноти та значимості зв’язку між змінними моделі.

3. Оцінка точності моделі

4. Перевірка значущості та довірчі інтервали

5. Прогнозування за лінійною моделлю

1. Прості лінійні регресійні моделі

Прості лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною змінною (Y) та розглядається як функція від незалежної змінної (X).

У загальному вигляді проста вибіркова регресійна модель запишеться так:

Y = a₀ + a₁ X + u, (1)

де Y – вектор спостережень за залежною змінною;

X – вектор спостережень за незалежною змінною;

a₀, a₁ – невідомі параметри регресійної моделі;

u – вектор випадкових величин (помилок).

У загальному матричному вигляді економетрична модель записується так:

Y=AX+u, (2)

де А – матриця параметрів моделі розміром m×n (m – кількість незалежних змінних, n – число спостережень);

Y – матриця значень залежної змінної;

Х – матриця незалежних змінних;

u – матриця випадкової складової.

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Отже, модель (2.1) є лінійною регресійною моделлю.

Розглянемо приклад.

Маємо вибірку даних за 8 років, які характеризують продуктивність праці (Y_факт) групи однорідних підприємств в залежності від простоїв основного обладнання (Х). Побудувати парну лінійну регресійну модель виду Y=₀+₁X.

Щоб мати явний вид залежності, необхідно знайти (оцінити) невідомі параметри цієї моделі.

Дані наведені в табл.1.

Таблиця 1.

№ заводу	Продуктивність праці, тис.грн./чол.	Простої основного обладнання, год./рік;
	Yфакт	Х
1	2,4	67
2	3,6	64
3	8,2	8
4	6,7	33
5	7,5	7
6	7,2	28
7	7,5	17
8	8,0	12

Реальні спостереження Y_факт зобразимо точками у системі координат (Х,Y) (мал.1).

Малюнок 1. Залежність продуктивності праці від простоїв основного обладнання

Візуально можна припустити, що між даними є лінійна залежність, тобто їх можна апроксимувати прямою лінією.

Малюнок 2.

Через множину спостережуваних точок можна провести необмежену кількість прямих Y = _ + ₁x.

y

Y _факт

u_i

Y_розр

Y=₀ +₁x_i

x_i x

Малюнок 3.

На мал. 3, пряма розташована таким чином, що деякі точки знаходяться вище, деякі нижче прямої, на основі чого можна встановити відхилення (помилки) відносно цієї прямої:

Французький математик Лежандром у XIX ст. запропонував метод знаходження теоретичної лінії, наближеної до фактичних даних як мінімальну суму (S) квадратів відхилення їх ординат Y_i від теоретичних значень Y:

З цього і назва методу – метод найменших квадратів (або скорочено 1МНК).

Відхилення, або помилки, ще інколи називають залишками. Треба проводити пряму таким чином, щоб сума квадратів помилок була мінімальною:

(3)

Визначимо значення _о та _, які мінімізують вираз (3). Мінімум функції (3) досягається за необхідних умов, коли перші похідні дорівнюють нулеві, тобто

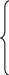
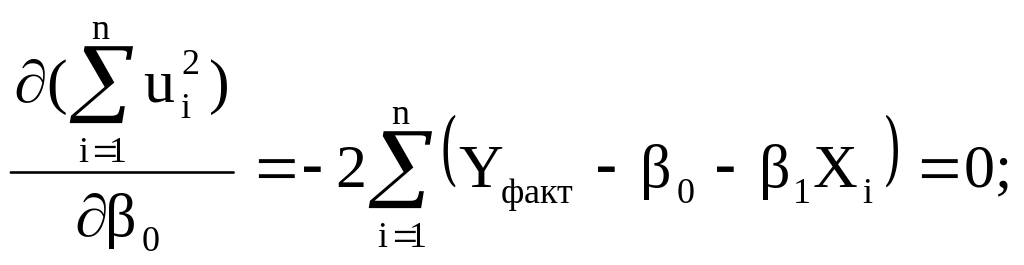
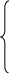
Звідки отримаємо систему лінійних рівнянь:

яка називається нормальною.

Всі суми, що входять в систему, обраховуються на основі вхідних статистичних даних.

Таблиця 2

	Yфак	X1	(X1)2	Y*X1
	2,4	67	4489	160,8
	3,6	64	4096	230,4
	8,2	8	64	65,6
	6,7	33	1089	221,1
	7,5	7	49	52,5
	7,2	28	784	201,6
	7,5	17	289	127,5
	8	12	144	96
S	51,1	236	11004	1155,5

На основі обчислених згідно з вхідними даними табл.2 дістанемо систему рівнянь:

В результаті рішення системи отримуємо значення:

₀ = 8,96,

₁ = – 0,087.

Таким чином, економетрична модель продуктивності праці (рівняння регресії) буде мати вид:

Y_розр = 8,96 – 0,087  Х