Контрольные вопросы

1. Что такое случайное событие, случайная величина, дискретная случайная величина, непрерывная случайная величина?

2. Что такое варианта, статистическая совокупность, частота, частость, закон распределения?

3. Что такое гистограмма, полигон? Какими свойствами они обладают?

4. Назовите основные параметры экспериментального распределения.

5. Что такое теоретическое распределение, каковы его параметры?

6. Каков смысл дифференциальной и интегральной функций нормального распределения? Как они выражаются на графике дифференциальной функции?

7. Какова связь между параметрами генеральной и выборочной совокупности?

8. Каков смысл параметрических критериев?

9. В чем заключается смысл c-критерия?

Список литературы

1. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. М.: Наука, 1970.

2. Гмурман В.Е. Теория вероятностей и математическая статистика : учеб.пособие для вузов. М.:Высш.шк., 2004.479с.

3. Гусак А.А.Высшая математика т.2 : учебник для студентов вузов. Мн.:ТетраСистем, 2001.448с.

4. Физический практикум / Под ред. В.И. Ивероновой. М.: Гос. изд-во физико-математической литературы, 1962. 956с.

Лабораторная работа 2-2

Молекулярное строение жидкостей и методы определения коэффициента поверхностного натяжения

Цель работы: познакомиться с молекулярно-кинетической теорией газов и жидкостей и изучить капиллярный эффект и явление поверхностного натяжения.

Задача работы: определить коэффициент поверхностного натяжения исследуемой жидкости несколькими методами.

Теоретическая часть

Структура жидкостей

В газах и жидкостях, в отличие от твердых тел, молекулы не связаны между собой стационарными устойчивыми связями. В газах расстояние между молекулами в среднем большое, и молекулы практически свободно изменяют взаимное расположение. В жидкостях расстояние между молекулами малое, молекулы плотно заполняют занимаемое жидкостью пространство и сравнительно медленно меняют взаимное положение. В течение продолжительных промежутков времени группы молекул могут образовать агрегаты молекул, которые по своим свойствам напоминают твердое тело. Таким образом, жидкости по своей структуре и межмолекулярным силам имеют как свойства газа, так и свойства твердых тел. В связи с этим теория строения жидкостей является наиболее трудной и наименее разработанной.

Потенциал межмолекулярного взаимодействия

Взаимодействие молекул удобно характеризовать зависимостями силы f(r) и потенциальной энергией взаимодействия U(r), как функциями расстояния r между центрами сблизившихся молекул, приведенными на рис. (2-2.1 и 2-2.2).

При построении этих кривых сила взаимодействия и потенциальная энергия молекул, находящихся на бесконечно большом расстоянии друг от друга, положены равными нулю. На расстояниях r>r₀(рис. 2-2.1) между молекулами действуют силы взаимного притяжения (отрицательный знак силы), а при r<r₀ силы отталкивания (положительный знак силы).

Из рис. 2-2.1 видно, что по абсолютному значению сила притяжения растет с увеличением r вплоть до некоторого значения r₁. Затем сила уменьшается и при расстоянии r₀ между атомами становится равной нулю. При дальнейшем уменьшении r сила вновь появляется, но уже сила отталкивания, быстро растущая с уменьшением расстояния между молекулами, стремясь к бесконечности при .

Кривой f(r) соответствует похожая на нее кривая U(r) (рис. 2-2.2). Сходство кривых не должно удивлять, так как f и Uсвязаны, как известно, соотношением .

При расстоянии между атомами r₀, когда сила взаимодействия равна нулю, потенциальная энергия проходит через минимум. О молекуле в таком положении принято говорить, что он находится на дне “потенциальной ямы”. Это положение равновесия, т. е. силы притяжения уравновешиваются силами отталкивания.

Какой-либо универсальной формулы U(r), пригодной для всех молекул, не существует. Более точно характеристика U(r) может быть дана лишь конкретно для данных молекул. Во многих вопросах теории к хорошим результатам приводит следующая аппроксимация функции U(r):

, (2-2.1)

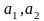в которой постоянные подбираются из требований наилучшей аппроксимации реального потенциала. Как показало исследование потенциалов, в большинстве случаев хорошим приближением являются n=12, m=6 при , уточняемых для конкретных атомов. Функция U(r), описываемая уравнением (2-2.1), называется потенциалом Леннарда–Джонса, широко используется в теории жидкостей и газов. Первый член (2-2.1) соответствует силам отталкивания, второй – силам притяжения, которые называются силами Ван-дер-Ваальса.

В теории уравнения состояния Ван-дер-Ваальса применяется более грубая аппроксимация. Крутой участок кривой U(r) заменяется вертикальной прямой, как это изображено на рис. 2-2.2 пунктиром. Если d – расстояние этой прямой от начала координат, то центры взаимодействующих частиц не могут сблизиться на расстояние, меньше d. Расстояние d играет роль диаметра молекулы, который относится к числу не вполне четко определяемых величин.

Рассматриваемая аппроксимация соответствует модели твердых упругих шаров, между которыми действуют силы притяжения; силы отталкивания учитываются тем, что размеры шаров считаются конечными.