Определение коэффициентов уравнения регрессии.
Некоторые свойства матрицы планирования:
Сумма всех безразмерных значений параметров.
Эти свойства положены в основу расчета коэффициентов уравнения регрессии. При определении выражений для коэффициентов используется метод наименьших квадратов. К данному случаю метод наименьших квадратов запишется:
Для
свободного члена:
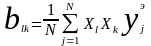
После
определения значения коэффициентов в
уравнении регрессии производится
проверка значимости коэффициентов по
условию:
,
где
– оценка
дисперсии, с которой определяются
коэффициенты.
,
где
t – критерий Стьюдента.
Критерий Стьюдента находят из таблиц – по количеству степеней свободы и некоторой доверительной вероятности. Если коэффициент оказался незначимым, то его считают равным нулю, т.е. он исчезает из уравнения регрессии.
Далее
проводится проверка адекватности модели
(соответствие модели). Условие проверки:
критерий Фишера – расчетный должен
быть меньше или равен табличному.
(1)
Если нет проверки на воспроизводимость, то используют вместо формулы (1) используют формулу (2):
(2)
Дисперсия
адекватности:
,
где B – число значимых коэффициентов в уравнении регрессии, включая свободный член. Если коэффициент оказался незначимым (равен 0), то данный фактор не является влияющим).
Метод дробного факторного эксперимента.
Метод дробного факторного эксперимента – система опытов, представляющая собой часть ПФЭ, позволяющая рассчитать значения коэффициентов уравнения регрессии и уменьшить объем экспериментальных работ.
Суть метода состоит в том, что одну из переменных (независимую) заменяют величиной парного взаимодействия. Xi=XlXk. При этом возникают проблемы. Суть проблемы – выбрать произведение XlXk, которое не будет являться значимым, т.е. будет иметь незначимые члены уравнения регрессии.
Запись Xi=XlXk носит название генерирующего соотношения, обычно выбирается самим экспериментатором.
Число опытов в случае ДФЭ определится:
,где
q –
количество генерирующих соотношений.
В случае, когда построенная по методу ПФЭ регрессионная математическая модель не является адекватной (большая кривизна поверхности), следует ввести в рассмотрение члены ряда Тейлора (члены уравнения регрессии) более высоких порядков.
Известны следующие методы планирования экспериментов (регрессионного анализа), позволяющие определить коэффициенты при членах второго порядка:
Ортогональное, центральное, композиционное планирование.
Рототабельное центр. композиционное планирование.
Суть методов: кроме варьирования на верхнем и нижнем уровнях эксперименты осуществляется в центре плана (на базовом уровне) и в так называемых звездных точках за пределами плана ПФЭ.
Ценность статистических моделей:
Модель позволяет с высшей точностью описать процесс в области адекватности, в любых точках зоны адекватности (где проводились эксперименты). За пределами области адекватности модель требует дополнительного изучения.
Модель может служить основой для оптимизации. Дает возможность описать математически процесс, когда невозможно создать феноменологическую модель.