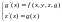2. Частное определение: суть интерполяции данных

3. Лабораторная работа: Сглаживание и фильтрация временных рядов.

Г рафик, построенный по экспериментальным данным, представляет собой очень ломанную кривую. Поэтому мы вынуждены сглаживать или усреднять, или фильтровать экспериментальные данные.

Стандартное построение графика по данным полученным опытным путем:

М 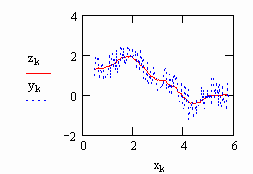етод скользящего среднего

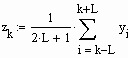
Экспоненциальное сглаживание ряда Y

!Условие:

10 Билет

1. Метод Эйлера решения обыкновенных дифференциальных уравнений.

В основе метода Эйлера лежит идея графического построения решения диф-ного уравнения. Этот метод одновременно дает и способ нахождения искомой функции в численной (табличной) форме.

И дея метода заключается в том, что на малом промежутке изменения независимой переменной 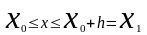(где h – шаг таблицы) интегральная кривая диф-ного уравнения заменяется отрезком прямой (касательной) . Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.

Рабочая формула для определения значения y имеет вид: 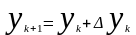, где , ,

2. Частное определение: суть аппроксимации данных

11 Билет

1. Метод Рунге-Кутта решения обыкновенных дифференциальных уравнений.

Метод Рунге-Кутта применяется также для приближенного решения систем обыкновенных дифференциальных уравнений. Пусть, например, дана система дифференциальных уравнений:

( 11)

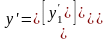
где

П од решением системы (11) понимается любая совокупность функций (y₁(x), y₂(x),…,y_n(x)), которая, будучи подставлена в уравнение (11), обращает их в тождества. Так как система дифференциальных уравнений имеет бесчисленное множество решений, то для выделения одного конкретного решения, кроме уравнения, нужны дополнительные условия. В простейшем случае задаются начальные условия

(12)

что приводит к задаче Коши.

2. Частное определение: определение невязки

БИЛЕТ 12

1.Метод Рунге-Кутта решения систем обыкновенных дифференциальных уравнений первого порядка.

Метод Рунге-Кутта. Пусть дано диф. Уравнение первого порядка: (1)с начальными условиями . Выберем шаг h и для кратности введем обозначения , , .

В вычислительной практике наиболее часто используется метод Рунге-Кутта.

По методу вычисляют 5 вспомогательных коэффициентов:

П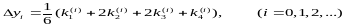 оследовательные приближения y_i искомой функции y определяются по формуле: где (5)

При достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта по формулам (большой), будет близким к точному.

2. Частное определение: определение временного ряда

13 Билет

1. Дифференциальные уравнения второго порядка как модель колебательных процессов. Математический маятник.

Математический маятник — гармонический осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Уравнение математического маятника без затухания (т.к. справа 0): , где w-собственная частота гармонического осциллятора. Уравнение вида - математический маятник с трением, где k – коэф. трения. Уравнение вида - с вынуждающей функцией.

Общее решение математического маятника: , с₁, с₂ – постоянные интегрирования. Пр.: При , -> и .

Приближённое решение математического маятника: Условие:

Пусть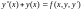 , где -трение маятника о воздух, или толчок маятника рукой. Пусть , тогда .

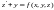Получаем систему:

Решение системы диф. уравнений методом Рунге-Кутта – простейшее решение математического маятника:

Для решения надо найти 8 коэффициентов (2 набора k и m):

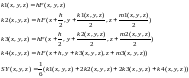
Для коэффициентов m в левой части k заменяем на m и SY на SZ, а в правой - F на G.

Составляем систему решений:

Основная идея численного метода решения дифференциального уравнения второго порядка - переход от див. уравнения n-го порядка к системе уравнений 1-го порядка:

Пр.: пусть . Обозначим , тогда . Подставим:

Пр.: 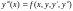Обозначим: Подставим

Ещё одна замена: Получаем: