
- •2. Частное определение: Определение фильтрации данных.
- •3 Билет
- •1. Методы аппроксимации табличных данных. Невязки. Метод наименьших квадратов.
- •2 . Частное определение: Определение гармонического анализа.
- •4 Билет
- •1. Поиск простейших эмпирических зависимостей при помощи среднеквадратичного приближения. Невязки.
- •5 Билет
- •6 Билет
- •7 Билет.
- •2. Частное определение: понятие о тренде в данных
- •3. Лабораторная работа: Расчет градиентов экспериментальных данных
- •8 Билет
- •1. Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных.
- •2. Частное определение: определение скользящего среднего
- •9 Билет
- •1. Дифференциальные уравнения первого и второго порядков: основные определения и способы решений. Общее и частное решения.
- •2. Частное определение: суть интерполяции данных
- •3. Лабораторная работа: Сглаживание и фильтрация временных рядов.
- •10 Билет
- •1. Метод Эйлера решения обыкновенных дифференциальных уравнений.
- •2. Частное определение: суть аппроксимации данных
- •11 Билет
- •1. Метод Рунге-Кутта решения обыкновенных дифференциальных уравнений.
- •2. Частное определение: определение невязки
- •1.Метод Рунге-Кутта решения систем обыкновенных дифференциальных уравнений первого порядка.
- •2. Частное определение: определение временного ряда
- •13 Билет
- •1. Дифференциальные уравнения второго порядка как модель колебательных процессов. Математический маятник.
- •2. Частное определение: определение характерного масштаба процесса.
- •14 Билет
- •1 . Задачи Коши для обыкновенного дифференциального уравнения. Физический смысл начальных условий. Пример на схеме метода Эйлера.
- •15 Билет
- •16 Билет
- •17 Билет
- •1. Критический путь сетевого графика.
- •18 Билет
- •1. Сетевые графики и метод календарного планирования
2. Частное определение: понятие о тренде в данных
3. Лабораторная работа: Расчет градиентов экспериментальных данных
С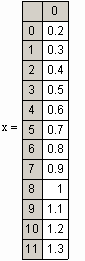
 уществует
несколько методов нахождения интеграла
такого рода экспериментальных данных.
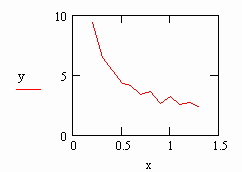
Начнем с того, что присвоим значения х
и у массивам данных и построим график
заданной таблично функции:
уществует
несколько методов нахождения интеграла
такого рода экспериментальных данных.
Начнем с того, что присвоим значения х
и у массивам данных и построим график
заданной таблично функции:

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
И![]() так,
рассмотрим первую наиболее грубую
методику нахождения численного значения
интеграла – метод прямоугольников.
Суть метода заключается в том, что график
функции по оси абсцисс разбивается на
n равных отрезков, каждый из которых
составляет нижнее основание прямоугольника.
Высота такого прямоугольника будет
равной значению функции в этой точке.
Количество таких прямоугольников не
может быть достаточно большим.
так,
рассмотрим первую наиболее грубую
методику нахождения численного значения
интеграла – метод прямоугольников.
Суть метода заключается в том, что график
функции по оси абсцисс разбивается на
n равных отрезков, каждый из которых
составляет нижнее основание прямоугольника.
Высота такого прямоугольника будет
равной значению функции в этой точке.
Количество таких прямоугольников не
может быть достаточно большим.
З![]() ная
формулу нахождения площади прямоугольника,
нетрудно рассчитать ее для n-числа таких
прямоугольников, что и даст, собственно,
в грубом приближении, площадь интегрируемой
функции:
ная
формулу нахождения площади прямоугольника,
нетрудно рассчитать ее для n-числа таких
прямоугольников, что и даст, собственно,
в грубом приближении, площадь интегрируемой
функции:
формула левых прямоугольников
ф![]()
![]() ормула
правых прямоугольников
ормула
правых прямоугольников
Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут вышеприведенные формулы. Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно.
Метод трапеций. Его отличие заключается в том, что верхнее основание является стягивающей интегрируемую функцию хордой – результат линейной интерполяции. Зная формулу площади, трапеции нетрудно посчитать сумму всех составляющих интегрируемую функцию трапеций, что позволит получить искомое численное значение интеграла:
![]()
![]()
8 Билет
1. Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных.
Формула Тейлора
Рассмотрим функцию f(x)

Ф. Тейлора является эффективным генератором получения формул для вычисления производных любого порядка.
Градиент:
Допустим, у нас есть измеренные данные
температуры T1…Ti
по времени t1...ti
, градиент исследуемой величины будет
рассчитываться

 общий
вид производной
общий
вид производной
В
общем трёхмерном случае градиент – это
вектор
 .
Но т.к. мы работаем с большими массивами
точек, то решать градиент в общем виде
сложно, мы рассматриваем градиент по
одной переменной – это есть производная
в i-точке
по направлению х.
.
Но т.к. мы работаем с большими массивами
точек, то решать градиент в общем виде
сложно, мы рассматриваем градиент по
одной переменной – это есть производная
в i-точке
по направлению х.
 .
.
2. Частное определение: определение скользящего среднего
М етод
скользящей
средней
заключается в том, что для каждого
аргумента берется средняя арифметическая
на несколько соседних значениях
етод
скользящей
средней
заключается в том, что для каждого
аргумента берется средняя арифметическая
на несколько соседних значениях
 ,
т.е.
,
т.е.
 ;
;
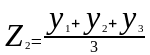 Пропадут
первые v-точки
и последние v-точки:
2v-точки.
Пропадут
первые v-точки
и последние v-точки:
2v-точки.
Применяют для длинных рядов, где пропажа двух крайних 2v-точек ничего не решает. Характерно для физ-географов и не характерно для эконом географов, которые работают с небольшими рядами. Многоцелевой, легко программируемый метод, однако велика вероятность неточности.
9 Билет
1. Дифференциальные уравнения первого и второго порядков: основные определения и способы решений. Общее и частное решения.
М етоды
решения обыкновенных дифференциальных
уравнений первого порядка вида
етоды
решения обыкновенных дифференциальных
уравнений первого порядка вида
Ч то
же касается дифференциальных уравнений
n-ого
порядка:
(4)
то
же касается дифференциальных уравнений
n-ого
порядка:
(4)
для которых задача Коши состоит в нахождении решения y=y(x), удовлетворяющего начальным условиям
 (5)
(5)

г де
–
заданные числа, то их можно свести к
системе дифференциальных уравнений
первого порядка. Так, например, уравнение
второго порядка
(6)
де
–
заданные числа, то их можно свести к
системе дифференциальных уравнений
первого порядка. Так, например, уравнение
второго порядка
(6)
м ожно
записать в виде системы двух уравнений
первого порядка при помощи стандартной
замены:
ожно
записать в виде системы двух уравнений
первого порядка при помощи стандартной
замены:
(7)
Методы решения систем обыкновенных дифференциальных уравнений основываются на соответствующих методах решения одного уравнения.
Очевидно, что ставить вопрос об отыскании приближенных значений интеграла или решения y(x) уравнения (1) можно в том и только в том случае, если решение y(x), удовлетворяющее условию (y(x0)=y0) , существует и единственно. Как известно из общей теории дифференциальных уравнений, для этого достаточно, чтобы фигурирующая в правой части уравнения (1) функция f(x,y) была непрерывна в рассматриваемой области по обоим аргументам и имела ограниченную частную производную.
