
- •2. Частное определение: Определение фильтрации данных.
- •3 Билет
- •1. Методы аппроксимации табличных данных. Невязки. Метод наименьших квадратов.
- •2 . Частное определение: Определение гармонического анализа.
- •4 Билет
- •1. Поиск простейших эмпирических зависимостей при помощи среднеквадратичного приближения. Невязки.
- •5 Билет
- •6 Билет
- •7 Билет.
- •2. Частное определение: понятие о тренде в данных
- •3. Лабораторная работа: Расчет градиентов экспериментальных данных
- •8 Билет
- •1. Общее представление о формуле Тэйлора. Численный расчет градиентов таблично заданных функций. Расчет старших производных.
- •2. Частное определение: определение скользящего среднего
- •9 Билет
- •1. Дифференциальные уравнения первого и второго порядков: основные определения и способы решений. Общее и частное решения.
- •2. Частное определение: суть интерполяции данных
- •3. Лабораторная работа: Сглаживание и фильтрация временных рядов.
- •10 Билет
- •1. Метод Эйлера решения обыкновенных дифференциальных уравнений.
- •2. Частное определение: суть аппроксимации данных
- •11 Билет
- •1. Метод Рунге-Кутта решения обыкновенных дифференциальных уравнений.
- •2. Частное определение: определение невязки
- •1.Метод Рунге-Кутта решения систем обыкновенных дифференциальных уравнений первого порядка.
- •2. Частное определение: определение временного ряда
- •13 Билет
- •1. Дифференциальные уравнения второго порядка как модель колебательных процессов. Математический маятник.
- •2. Частное определение: определение характерного масштаба процесса.
- •14 Билет
- •1 . Задачи Коши для обыкновенного дифференциального уравнения. Физический смысл начальных условий. Пример на схеме метода Эйлера.
- •15 Билет
- •16 Билет
- •17 Билет
- •1. Критический путь сетевого графика.
- •18 Билет
- •1. Сетевые графики и метод календарного планирования
2 . Частное определение: Определение гармонического анализа.
4 Билет
1. Поиск простейших эмпирических зависимостей при помощи среднеквадратичного приближения. Невязки.
Невязка – разница между эмпирическими значениями и значениями аппроксимирующих линий; или разница между наблюденными аппроксимирующих функций.
Поиск простейших эмпирических зависимостей необходим чтобы упорядочить значения системы, заменить одну систему координат на другую.
Z = axm
lnz = lna + m lnx соответственно Y = AX + B – линейная зависимость, а х = lnx и у = lnz – логарифмич замена.
В большинстве случаев, чем меньше невязка, тем аппроксимированное значение ближе к решению, то есть,
2. Частное определение: определение сглаживания данных
5 Билет
1. Общее представление о рядах Фурье. Гармонический анализ временных рядов
Ряд Фурье —
представление произвольной функции ![]() с
периодом
с
периодом ![]() в
виде ряда
в
виде ряда

Этот ряд может быть также переписан в виде
 .
.
где
![]() —
амплитуда k-го
гармонического колебания,
—
амплитуда k-го
гармонического колебания,
![]() —
круговая
частота гармонического колебания,
—
круговая
частота гармонического колебания,
![]() —
начальная
фаза k-го
колебания,
—
начальная
фаза k-го
колебания,
![]() — k-я
комплексная амплитуда
— k-я
комплексная амплитуда
2. Частное определение: суть аппроксимации данных
6 Билет
1. Сглаживание и фильтрация временных рядов. Определения и основные алгоритмы.
2. Частное определение: определение математического маятника
7 Билет.
1.Численное интегрирование временных рядов. Методы прямоугольников и трапеций. Погрешности.
З начение
определенного интеграла численно равно
площади криволинейной трапеции,
ограниченной графиком функции y=f(x),
осью абсцисс и прямыми х=а,
х=b.
Находя приближенно площадь криволинейной
трапеции, мы получаем значение интеграла.
Формально процедура численного
интегрирования заключается в том, что
отрезок [а, b]
разбивается на n
частичных отрезков, а затем подынтегральная
функция заменяется на нем легко
интегрируемой функцией, по определенной
зависимости интерполирующей значения
подынтегральной функции в точках
разбиения.
начение
определенного интеграла численно равно
площади криволинейной трапеции,
ограниченной графиком функции y=f(x),
осью абсцисс и прямыми х=а,
х=b.
Находя приближенно площадь криволинейной
трапеции, мы получаем значение интеграла.
Формально процедура численного
интегрирования заключается в том, что
отрезок [а, b]
разбивается на n
частичных отрезков, а затем подынтегральная
функция заменяется на нем легко
интегрируемой функцией, по определенной
зависимости интерполирующей значения
подынтегральной функции в точках
разбиения.
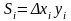 -
площадь левого прямоугольника
-
площадь левого прямоугольника
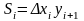 -
площадь правого прямоугольника
-
площадь правого прямоугольника
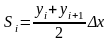 -
площадь трапеции
-
площадь трапеции
Итак,
функция у=f(x)
интегрируема на сегменте [a,b]
и требуется вычислить ее интеграл
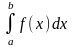 .
Составим интегральную сумму для f(x)
на сегменте [a,b]
. Для этого разобьем сегмент [a,b]
на n равных между собой
частей с помощью точек: x1,
x2, … ,
xk,
… , xn-1.
.
Составим интегральную сумму для f(x)
на сегменте [a,b]
. Для этого разобьем сегмент [a,b]
на n равных между собой
частей с помощью точек: x1,
x2, … ,
xk,
… , xn-1.
Если
длину каждой части мы обозначим через
х, так что
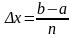 ,
то для каждой точки xiбудем
иметь:
,
то для каждой точки xiбудем
иметь:
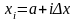 (i=0, 1, 2, …, n).
(i=0, 1, 2, …, n).
Обозначим
теперь через yi
значение подынтегральной
функции f(x)
при
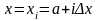 ,
то есть положим
,
то есть положим
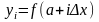 (i=0, 1, …, n).
(i=0, 1, …, n).
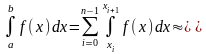
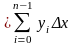 -
формула левых прямоугольников или
-
формула левых прямоугольников или
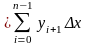 -
формула правых прямоугольников.
-
формула правых прямоугольников.
т.е (1)
и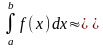 (1')
(1')
Эти приближенные равенства называются формулами прямоугольников.
В том случае, когда f(x)0, формулы (1) и (1’) с геометрической точки зрения означают, что площадь криволинейной трапеции aABb, ограниченной дугой кривой y=f(x), осью Ох и прямыми х=а и х=b, принимается приближенно равной площади ступенчатой фигуры, образованной из n прямоугольников с
основаниями и высотами: y0, y1, y2, …, yn-1 – в случае формулы (1), (рис.8) и y1, y2, y3, …, yn – в случае формулы (1') (рис.9).

У
yk-1
y1 B
y0 yn-1
A
0 a x1 xk-1 xn-1 b x
Рис.8

 Y
Y

 y1 B
y1 B

 yk
yn-1
yk
yn-1





 А
А


0 a x1 xk xn-1 b x
Рис.9
Исходя из приведенного выше геометрического смысла формул (1) и (1') способ приближенного вычисления определенного интеграла по этим формулам принято называть методом прямоугольников.
Метод трапеции
Простейшая из таких формул получается как среднее арифметическое правых частей формул (1) и (1'):
(4)
Л егко
усмотреть геометрический смысл этой
формулы. Если на каждом отрезке разбиения
дугу графика подынтегральной функции
y=f(x)
заменить стягивающей ее хордой (линейная
интерполяция), то мы получим трапецию,
площадь которой равна
егко
усмотреть геометрический смысл этой
формулы. Если на каждом отрезке разбиения
дугу графика подынтегральной функции
y=f(x)
заменить стягивающей ее хордой (линейная
интерполяция), то мы получим трапецию,
площадь которой равна
и

у
В
А
у0 у1 у2 уn-1 yn
0 a x1 x2 xn-1 b x
Рис.10
следовательно, формула (4) представляет собой площадь фигуры, состоящей из таких трапеций (рис.10) . Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.
Приведя в формуле (4) подобные члены, окончательно получим
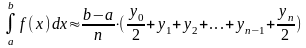
(5)
Формулу (5) называют формулой трапеций.
