9.7 Критерий оптимальности линейного частотного фильтра

Используя все полученные ранее соотношения, определим отношение сигнал/шум на выходе линейного стационарного частотного фильтра. Его частотный коэффициент передачи определяется по формуле:

Спектральная плотность полезного входного сигнала:

Используя спектральный метод анализа, можно определить значение выходного сигнала в любой момент времени t₀:

(16)

Белый шум на входе при любой частоте имеет постоянный энергетический спектр (или дисперсию):

Вообще, для любого сигнала энергетический спектр (или же квадрат АЧХ – модуля спектральной плотности) связан с его автокорреляционной функцией парой преобразований Фурье. Данная функция количественно определяет степень отличия сигнала s(t) и его сдвинутой на τ копии s(t – τ) и равна их скалярному произведению:

Тогда дисперсия (или энергетический спектр) шума на выходе фильтра определится как: (17)

Искомое отношение сигнал/шум на выходе фильтра, определяемое как модуль мгновенного значения полезного сигнала к среднеквадратичному уровню шума (14) при использовании неравенства Шварца (Коши-Буняковского)

(18)

для (16) и (17) можно записать следующим образом:

Полученное в скобках выражение есть ни что иное, как полная энергия полезного входного сигнала (равенство Парсеваля), поэтому отношение сигнал/шум на выходе фильтра можно записать в виде: (19)

Неравенство (19) определяет критерий оптимальности линейного частотного фильтра, суть которого заключается в том, что отношение сигнал/шум на выходе фильтра зависит только от отношения энергий полезного сигнала и шума на его входе.

Данное соотношение содержит полное решение поставленной задачи и позволяет, зная энергетические спектры сигнала и шума, так подобрать АЧХ фильтра, чтобы получить ощутимый выигрыш.

9.8 Согласованный линейный фильтр

Частотно-избирательную систему, выполняющую обработку суммы сигнала и шума некоторым наилучшим образом, называют оптимальным линейным фильтром.

Зафиксируем некоторый произвольный момент времени t₀ и постараемся так выбрать значения функции h(t), чтобы величина |s_вых(t₀)| достигла максимального возможного значения. Если такая функция действительно существует, то отвечающий ей линейный фильтр называют фильтром, согласованным с заданным входным сигналом или согласованным фильтром.

Отклик на выходе фильтра, подлежащий максимизации по модулю:

s_вых(t₀) = ∫ s_вх(τ) h(t₀ - τ) dτ. (20)

На основании неравенства Коши-Буняковского (18) для двух любых произвольных функций

(21)

Знак равенства, т.е. максимальное значение выходного сигнала, имеет место тогда, когда сомножители в подынтегальном выражении пропорциональны друг другу:

h(t₀ – τ) = ks_вх(τ), (22)

где k - произвольный коэффициент.

Выполняем формальную замену переменной t = t₀ - τ, получим

h_согл (t) = k s_вх(t₀ - t). (23)

Таким образом, импульсная характеристика согласованного фильтра представляет собой масштабную копию входного сигнала, которая располагается в зеркальном порядке вдоль оси времени. Помимо этого, импульсная характеристика согласованного фильтра смещена относительно входного сигнала s_вх(-t) на отрезок t₀ .

Рис. 9.6 иллюстрирует принцип построения функции h_согл(t) применительно к некоторому импульсному сигналу s_вх(t) длительностью τ_и, возникающему при t=0.

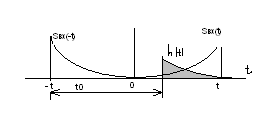
Рис. 9.6 – Построение импульсной характеристики согласованного фильтра

Анализируя данное построение, можно сформулировать необходимое условие физической реализуемости согласованного фильтра: промежуток t₀ между началом импульса на входе и моментом возникновения максимальной выходной реакции должен быть не меньше длительности выделяемого импульса, т.е. t₀ ≥ τ_и. В противном случае импульсная характеристика системы была бы отличной от нуля при t < 0, т. е. до момента поступления дельта-импульса на вход фильтра.