2. Построение годографа

При графическом представлении комплексных частотных характеристик (КЧХ) Н(jω) цепи обычно отдельно строят графики АЧХ Н(ω) и ФЧХ φ_н(ω). Однако комплексную частотную характеристику можно представить на одном графике. Такой график называется годограф КЧХ и строится он в комплексной плоскости. Годограф КЧХ представляет собой геометрическое место точек концов вектора комплексной функции Н(jω) на комплексной плоскости при изменении частоты ω от 0 до ∞ (рис.1.6). Годограф иногда называют амплитудно-фазовой характеристикой цепи. График годографа позволяет одновременно судить как об АЧХ, а также об ФЧХ комплексной частотной характеристики.

Для построения годографа строится декартовая система координат, при этом, по оси X откладывают реальную составляющую Re[Н(jω)] КЧХ, а по оси Y откладывают мнимую составляющую Jm[Н(jω)] КЧХ. На годографе указывают точки, соответствующие некоторым значениям частоты ω, и стрелкой показывают направление перемещения конца вектора Н(jω) при увеличении частоты. График годографа можно строить двумя способами.

По первому способу для построения графика можно использовать результаты расчета АЧХ Н(ω) и ФЧХ φ_н(ω), а точки графика годографа для заданного значения частоты ω_i наносить на комплексную плоскость аналогично тому, как это делается при построении графика в полярной системе координат.

П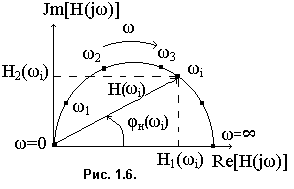 о второму способу необходимо комплексную частотную характеристику Н(jω) записать в алгебраической форме Н(jω) = Re[Н(jω)] + jJm[Н(jω)], затем для определенных частот ω_i рассчитать значения Re[Н(jω)] = Н₁(ω_i) и Jm[Н(jω)] = Н₂(ω_i), и затем, как обычно, нанести эти точки на плоскость и соединив их, получить график.

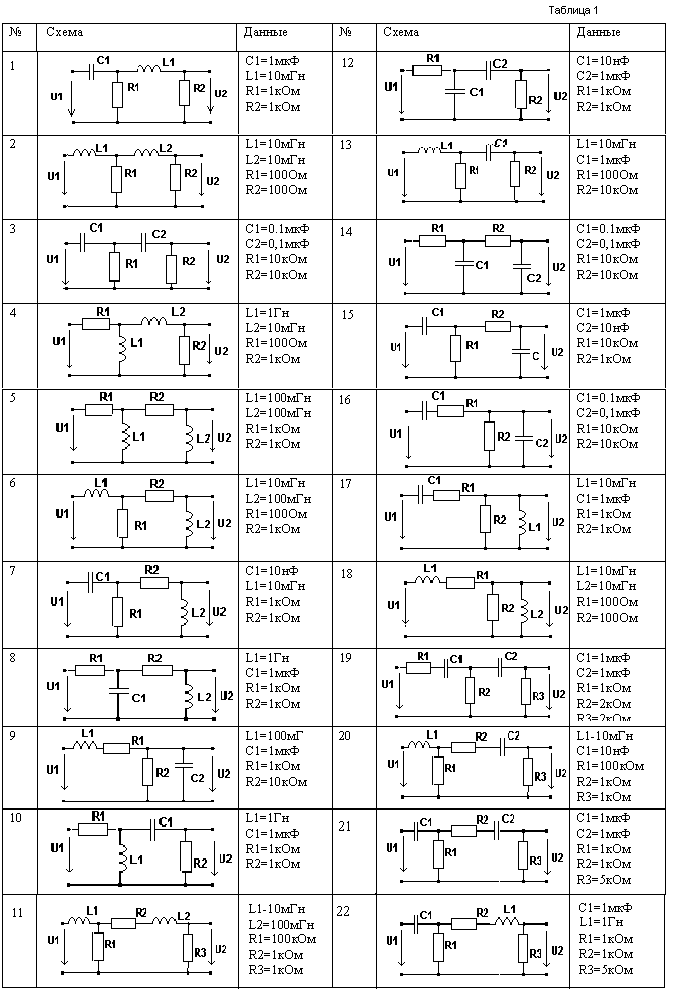
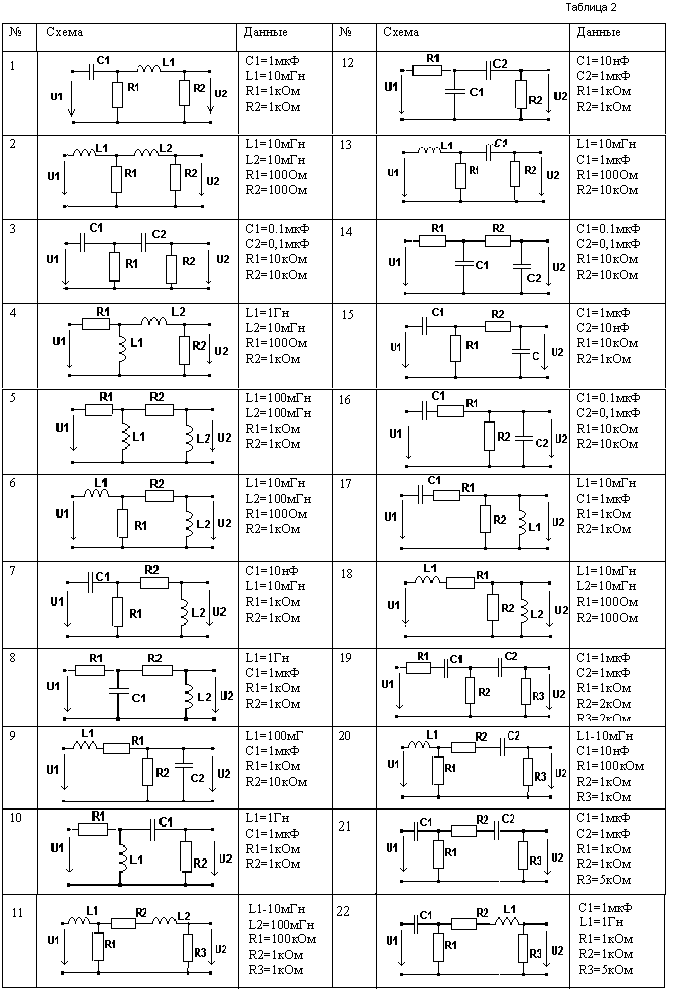
ЗАДАНИЕ 1. Расчет частотных характеристик электрической цепи.

1. Для электрической цепи, представленной в таблице 1, в соответствии с номером своего варианта рассчитать:

а) комплексную функцию входного сопротивления Z_ВХ(j), его амлитудно-частотную характеристику Z_ВХ() и фазо-частотную характеристику _z.

в) комплексную функцию частотного коэффициента передачи напряжения K_U(j), его АЧХ K_U() и ФЧХ _к ().

2. Построить графики Z_ВХ(), _z, K_U(), _к при заданных номиналах элементов схемы в абсолютном и логарифмическом масштабах.

3. Построить годографы Z_ВХ(j), K_U(j).

4. Определить характерные (резонансные) частоты.

5. Качественно объяснить вид построенных зависимостей.

ЗАДАНИЕ 2. Расчет линейной цепи при импульсном воздействии.

1. Для заданной электрической цепи рассчитать классическим и операторным методом импульсную и переходную характеристики.

2. Построить графики импульсной и переходной характеристики.

3. Определить по графикам параметры импульсной и переходной характеристик: постоянные времени , время установления t_уст (на уровне 0,9) и сравнить их с расчетными.

4. Качественно объяснить характер полученных характеристик.

Задание 3. Экспериментально, посредством моделирования заданной цепи в программе Electronics Workbench (EWB), определить рассчитанные характеристики.

1. Составить схемы измерений частотных и переходных характеристик: Z_ВХ() и _z; K_U(ω) и φ_k (ω); h(t); g(t) с использованием приборов электронной виртуальной лаборатории Electronics Workbench (EWB).

2. Привести графики характеристик, полученных в результате измерений.

3. Провести анализ соответствия результатов аналитического расчета и эксперимента.

Примечание: варианты заданий из таблицы выбирать в соответствии со своим порядковым номером по списку.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Как определяется функция комплексного входного сопротивления цепи и в чем ее физический смысл?

2. Как определяются АЧХ и ФЧХ комплексного входного сопротивления?

3. При каких условиях реакцию линейной системы на короткий входной импульс можно считать импульсной характеристикой системы?

4. Как связаны между собой импульсная характеристика системы и ее частотный коэффициент передачи?

5. Какими способами можно определить частотный коэффициент передачи линейной стационарной системы? Выберите из них оптимальный, на Ваш взгляд, способ.

6. В каких логарифмических единицах выражается усиление сигнала в системе?

7. При каких условиях RC-цепь можно считать дифференцирующей, а при каких – интегрирующей?

8. Исследуйте аналогичные условия (дифференцирования и интегрирования) для RL-цепи.

9. Поясните принципы построения годографа и его практическую значимость.