6.3. Связь линейных перемещений и
Вернемся к соотношению (1.5.10):
. (1.5.10)
Преобразуем его правую часть, учитывая, что из (1.5.5):
, , (1.5.5)
можем записать равенства
,
.
Подставляя их в правую часть (1.5.10):
, (1.5.10)
придем к следующему представлению линейного перемещения :
.
Сопоставляя его с (1.5.12)
, (1.5.12)
получаем искомую связь линейных перемещений по контравариантной координате с линейными перемещениями по криволинейной координате :
, .
Здесь коэффициенты Ламе вычисляются в точке .
Эта связь формулируется следующим образом.
Дифференциал контравариантной координаты равен произведению коэффициента Ламе, вычисленного в точке , на дифференциал криволинейной координаты .
6.4. Связь дифференциала дуги траектории с криволинейными координатами
При естественном способе задания движения точки ее траектория может задаваться с использованием криволинейных координат.
Параметрическое задание траектории в таком случае имеет вид
,
,
,
,
где
— дважды
непрерывно дифференцируемые на
промежутке 
функции.
Для того чтобы перейти к естественному способу задания движения, требуется построить естественную параметризацию траектории.
Для
этого, как показано в §2, необходимо
определить связь длины дуги с параметром 
,
являющимся внутренней переменной
заданной траектории.
Искомая
связь будет установлена, если укажем
зависимость дифференциала 
длины дуги от дифференциала 
внутренней переменной.
С
целью решения поставленной задачи
построим параметризацию 
траектории, заданной параметрически
функциями
.
Параметризацию получим, если подставим в (1.5.1):
(1.5.1)
вместо
криволинейных координат 
координатные функции
,
соответственно.
В результате придем к следующему векторному соотношению
, (1.5.13)
которое при каждом значении задает положение в пространстве точки , имеющей криволинейные координаты на заданной траектории.
А тогда можем записать
,
где
— линейное перемещение точки
по кривой
.
Из (1.5.13) находим
,
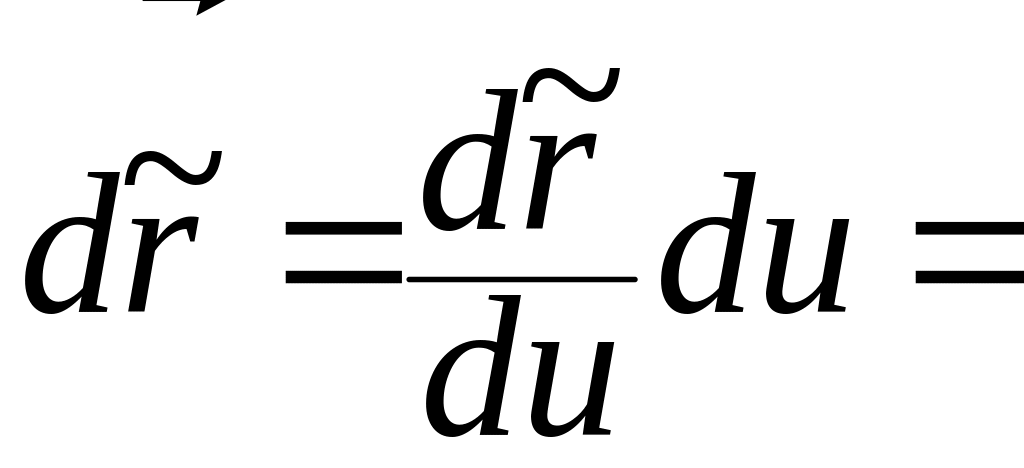
и, следовательно,
. (1.5.14)
Здесь
— метрические коэффициенты основной системы координат,
и
— коэффициенты
Ламе.
Все коэффициенты вычисляются в произвольном положении точки на заданной кривой.
Если не фиксировать траекторию точки (считать ее произвольной), то, учитывая, что линейное перемещение связано с линейными перемещениями криволинейных координат соотношением
,
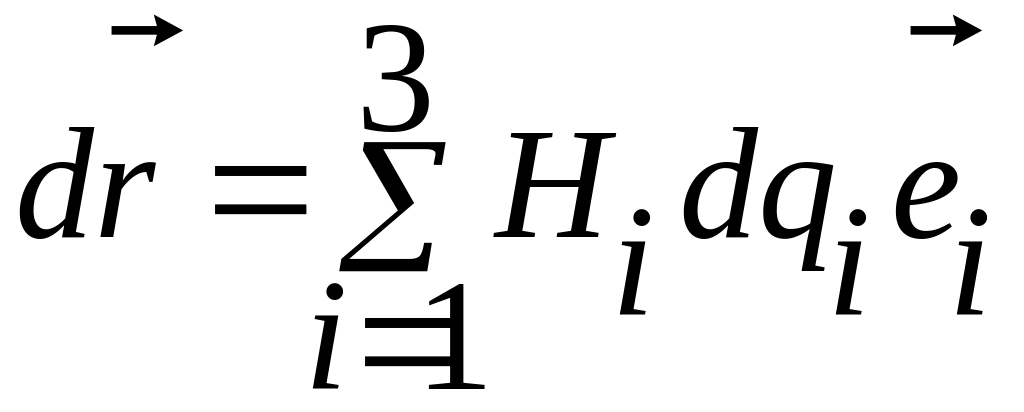получим следующее выражение для дифференциала дуги на любой траектории:
В нем следует положить
,
,
,
в том случае, когда траектория фиксирована и определяется криволинейными координатами
, , .
В результате такой замены придем к соотношению (1.5.14)
. (1.5.14)