4º. Коэффициенты Ламе. Основная система координат. Контравариантные координаты

4.1. Основная система координат

Зафиксируем точку  с криволинейными координатами .

Введем следующую аффинную систему координат (см. рис.1.5.3):

• Начало ее совпадает с точкой  .

• Первая координатная ось совпадает с касательной в точке  к первой координатной линии.

• Вторая координатная ось совпадает с касательной в точке  ко второй координатной линии.

• Третья координатная ось совпадает с касательной в точке  к третьей координатной линии.

На рисунке 1.5.3 координатная ось с номером  обозначена , . Координатная линия с номером обозначена . Координатная поверхность с номером  обозначена  . Координатные линии выделены жирным цветом.

Так как — дважды непрерывно дифференцируемая функция, то функция будет также дважды непрерывно дифференцируемой по  .

Рис. 1.5.3

Аналогичное утверждение справедливо для функции относительно  и для функции относительно  . Поэтому касательные к координатным линиям в точке существуют.

Направляющие векторы этих касательных будут коллинеарны, соответственно, векторам

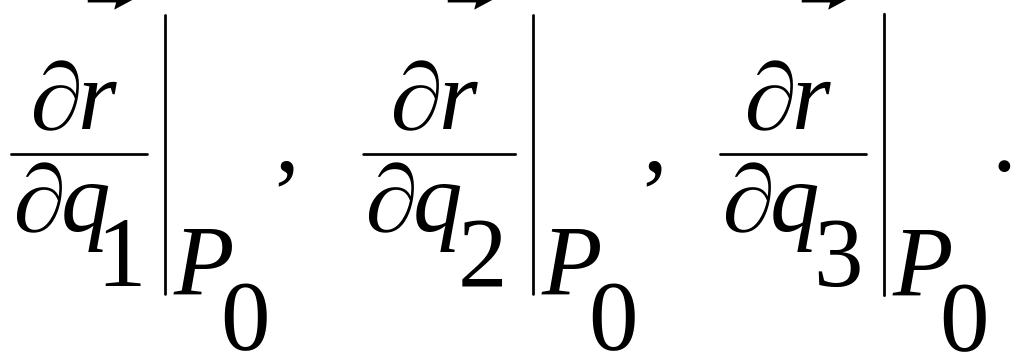
Здесь выражение означает, что вектор вычислен в точке с координатами .

В силу условия (1.5.2):

, (1.5.2)

векторы ,  ,  в точке будут некомпланарными.

Обозначим орты этих векторов ,  . Тогда можем записать:

, , (1.5.5)

где

.

Очевидно, вектор указывает направление изменения положения точки относительно точки при возрастании координаты  .

Определение 3

Величина называется коэффициентом Ламе, соответствующим криволинейной координате .

Тройка единичных векторов  , построенная по формуле (1.5.5) по криволинейным координатам  точки , является линейно независимой.

Поэтому можно принять ее в качестве базиса аффинной системы координат с полюсом в точке  .

Будем обозначать такую систему  .

Определение 4

Аффинную систему координат с базисом будем называть основной системой координат, соответствующей криволинейным координатам , а координаты произвольной точки  в этой системе — контравариантными координатами точки .

Из определения 1 (криволинейных координат), формулы (1.5.5) и определения 4 (основной системы) следует, что:

основная система координат  существует в любой в точке  .

Положение ее полюса  относительно точки отсчета  в абсолютном пространстве и базис однозначно определяются по формулам (1.5.1) и (1.5.5):

, (1.5.1)

, , (1.5.5)

при любых фиксированных значениях криволинейных координат  из области  .