1. Вычислим базис криволинейных координат в произвольной точке

, .

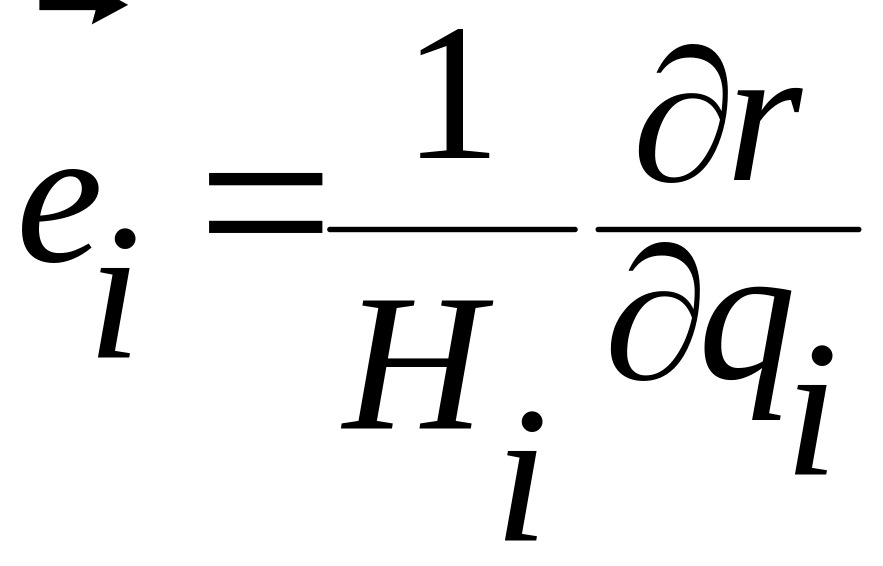Для этого находим коэффициенты Ламе:

.

Подставляя формулы (1.6.1) для :

, , , , (1.6.1)

и вычисляя производные по , получим

.

Аналогично вычисляются ,  :

, .

А тогда легко находим базисные векторы:

,

,

.

( )

( )

( )

Рис. 1.6.1.

Направления векторов показаны на рис.1.6.1.

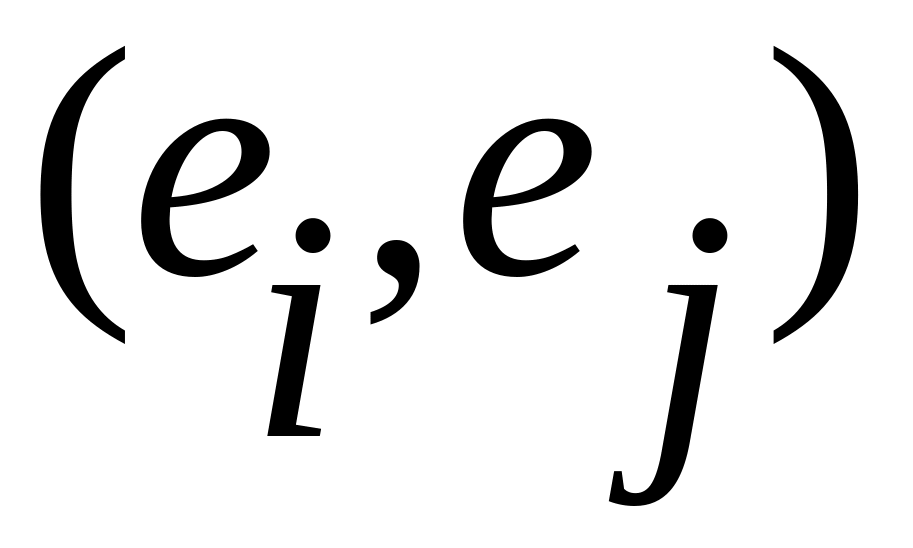2. Непосредственным вычислением и для легко показать, что векторы образуют ортонормированный базис, т.е. цилиндрическая система координат — это ортогональная криволинейная система координат.

3. Вычислим скорость в проекциях на орты .

Поскольку цилиндрическая система координат ортогональная, то

, , .

А тогда, поскольку , получаем

,

,

,

,

.

Из последней формулы легко находятся направляющие косинусы в декартовой системе координат

,

,

.

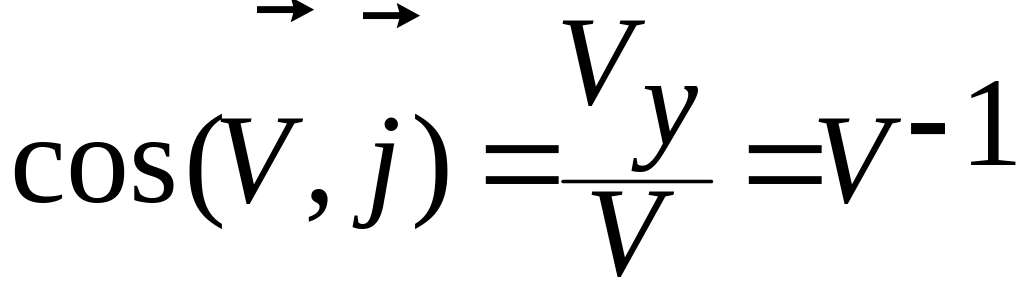
4. Вычислим ускорение в проекциях на орты .

Применим формулу Лагранжа.

Для этого определим функцию :

.

Отсюда находим

, .

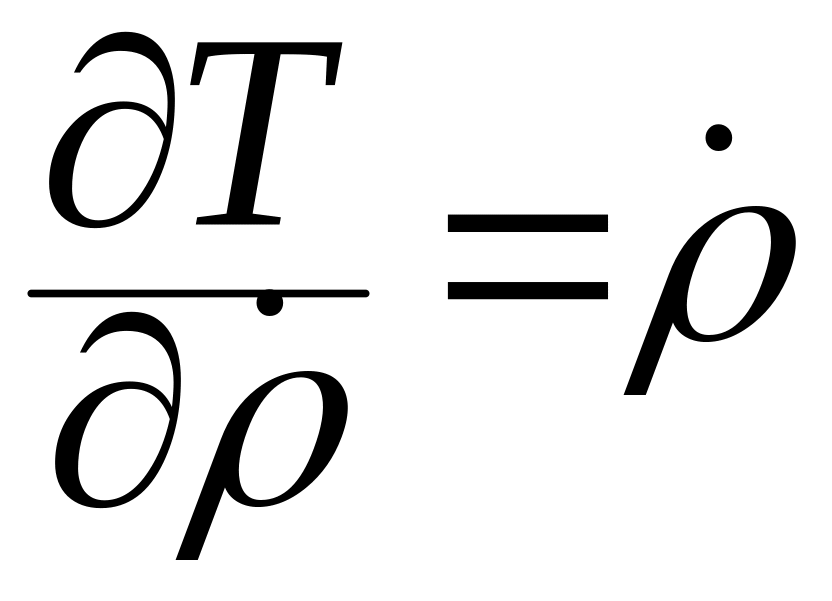Согласно формуле Лагранжа имеем

.

Следовательно,

.

Проведя аналогичные расчеты для координат и , получим:

• для координаты

, ,

,

или

,

• для координаты

, ,

или

.

Тогда для будем иметь

.

Направляющие косинусы в системе будут выражаться по формулам:

,

,

.

Формулы для направляющих косинусов вектора и вектора получены проектированием на орты векторов

;

.

2.2. Дополнение 2 к главе 1

§7. Кинематические характеристики точки в сферических координатах.

Как показано в §5, формулы связи декартовых и сферических координат имеют вид:

,

,

,

.

Полагаем

.