8.4. Понятие производной от функции вдоль движений точки

Вычислим производную  от функции и обозначим ее .

Пусть задано движение точки  в криволинейных координатах

, . (1.5.33)

Определим значения функции  , которые она может принимать на движении (1.5.33).

Ясно, что эти значения задаются вектор-функцией  , которая получается заменой в аргументов на правые части (1.5.33).

Сделав такую замену, вычислим производную по от построенной функции :

. (1.5.34)

Функция , стоящая в левой части (1.5.34), имеет смысл скорости изменения функции  вдоль движения (1.5.33).

В правой части (1.5.34) указывается ее аналитический вид, построенный по правилам дифференцирования по времени  функции  как сложной функции, в которой аргументы  ,  , задаются движением (1.5.33).

Как известно, правило дифференцирования сложной функции предполагает выполнение следующих операций.

1. Вычисление частных производных от функции  .

В результате получают три функции,

, ,

зависящие от трех переменных  .

2. Каждая функция 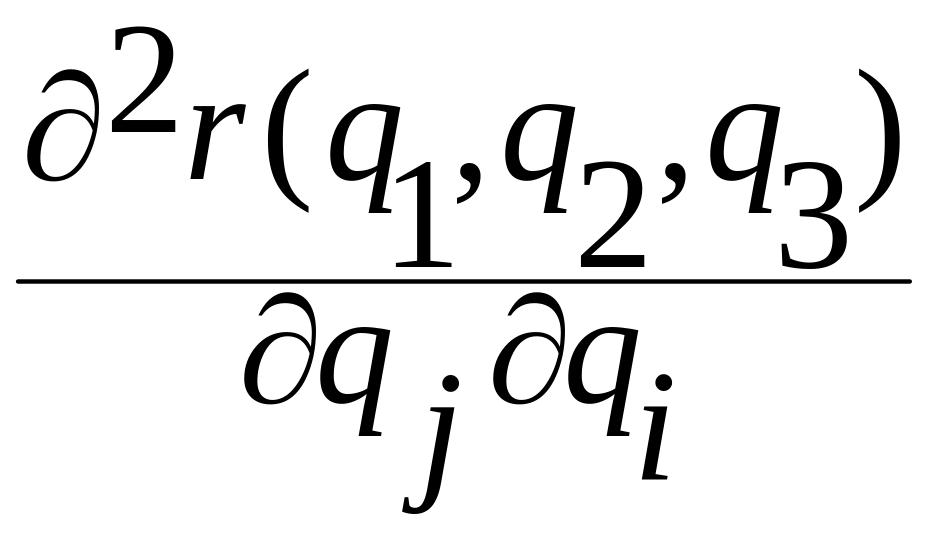 с номером  умножается на переменную  , и производится суммирование по всех построенных произведений.

В результате будет построена функция, зависящая от шести переменных и .

Будем записывать эту функцию в операторной форме или, что то же самое, в форме  .

В явном выражении этот оператор принимает вид:

. (1.5.35)

3. В построенной на этапе 2 функции (1.5.35) переменные  заменяются функциями 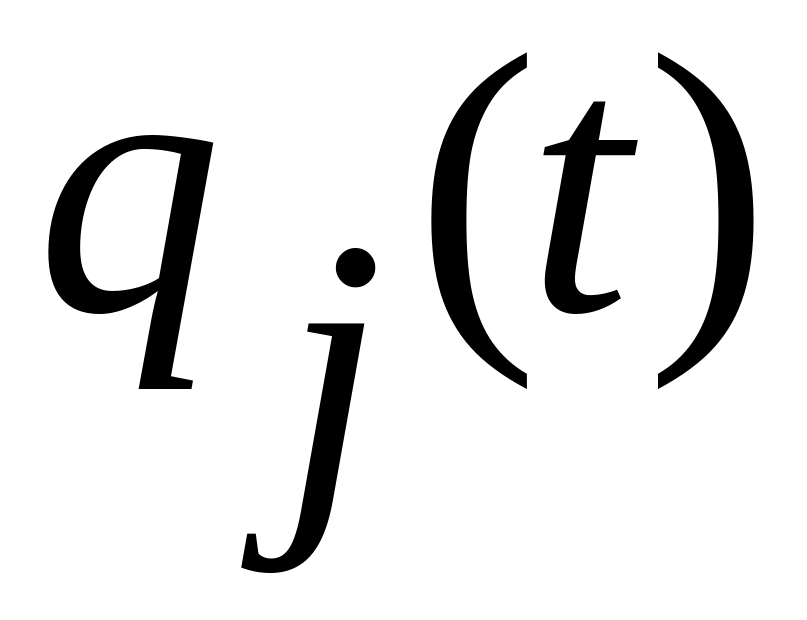 , а переменные  — производными 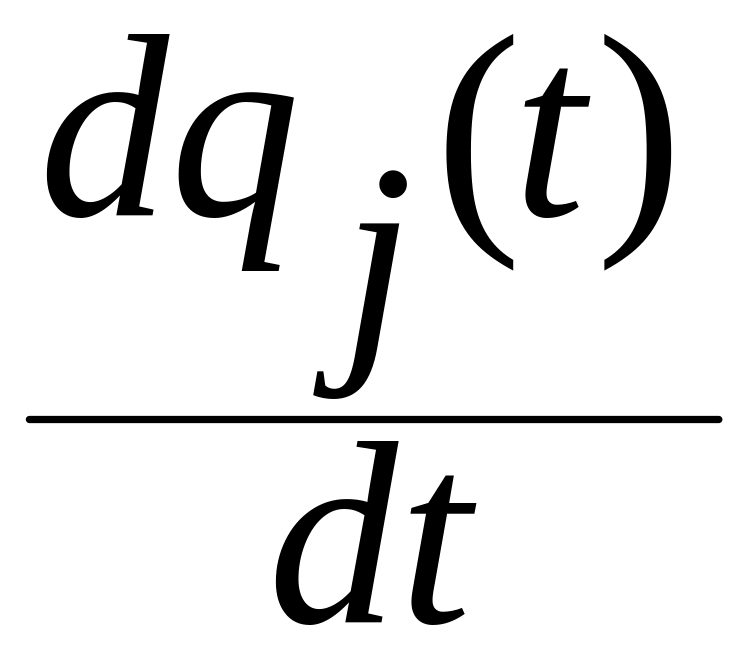, , где — правые части (1.5.33), определяющие заданное движение материальной точки.

Результатом произведенных действий, описанных на этапах 1,2,3, является функция, зависящая только от одной независимой переменной — от времени  , и она совпадает с правой частью равенства (1.5.34):

. (1.5.34)

Однако обратимся к функции (1.5.35):

, (1.5.35)

которая построена в процессе вычислений на этапе 2.

Определение 11

Функция, определяемая правой частью (1.5.35), называется производной от функции  вдоль движений механической системы и обозначается  .

В отличие от функции (1.5.34), функция (1.5.35):

(1.5.35)

зависит от шести переменных  и .

Из ее построения следует, что подстановкой в нее вместо любого фиксированного движения материальной точки, заданного в криволинейных координатах, и подстановкой в нее вместо — обобщенных скоростей на данном фиксированном движении, будет определена скорость изменения функции  вдоль этого фиксированного движения.

Таким образом, зная функцию (1.5.35), можно определить скорость изменения функции  на любом заданном движении, а не только на движении (1.5.33).

Поэтому функция (1.5.34) играет в дальнейшем важную роль.

Отметим, что функция, стоящая в правой части равенства (1.5.35), получена на основе действий, описанных в первых двух этапах вычисления производной по времени  от функции  .

В таких случаях говорят, что

«она получена дифференцированием функции  вдоль движений (на движениях) материальной точки».

Применительно к ее обозначению  , записанному в левой части (1.5.35), также говорят, что

«в левой части равенства (1.5.35) дифференцирование функции по времени  производится вдоль движений материальной точки».

В указанных случаях результат дифференцирования, т.е. правая часть равенства (1.5.35), задающая явный вид построенной функции, как правило, не приводится.