2. Первый способ (метод Хичкока)

В табл. 2 записываются все исходные данные задачи. Расстояния между грузообразующими и грузопоглощающими точками заносятся в отчеркнутые правые углы клеток. Эта таблица называется матрицей распределительного метода.

Распределение груза по потребителям производится начиная с грузоотправителя А₁ и грузополучателя В₁ т. е. с клетки А₁В₁. Потребность в грузе потребителя В₁ удовлетворяется полностью грузоотправителем А₁. В клетку А₁В₁ табл. 2 записывается весь объем потребления грузополучателя В_І — 200 т. Оставшийся в точке А₁ груз в количестве 200 т будет вывозиться потребителю В₂. Но потребителю В₂ нужно завезти не 200, а 400 т груза. Недостающие 200 т груза можно возить от грузоотправителя А₂. Оставшиеся у грузоотправителя А₂ 400 т груза можно вывезти в точку В₃ и т. д. Рассуждая таким образом, распределим весь груз по потребителям.

В табл. 2 распределение груза по потребителям (закрепление потребителей за грузоотправителями) выразится в заполнении соответствующих клеток (А1В1 А_ІВ₂, А₂В₂; А₂В₃; А₃В₃; А₃В₄).

Таблица 2 ;

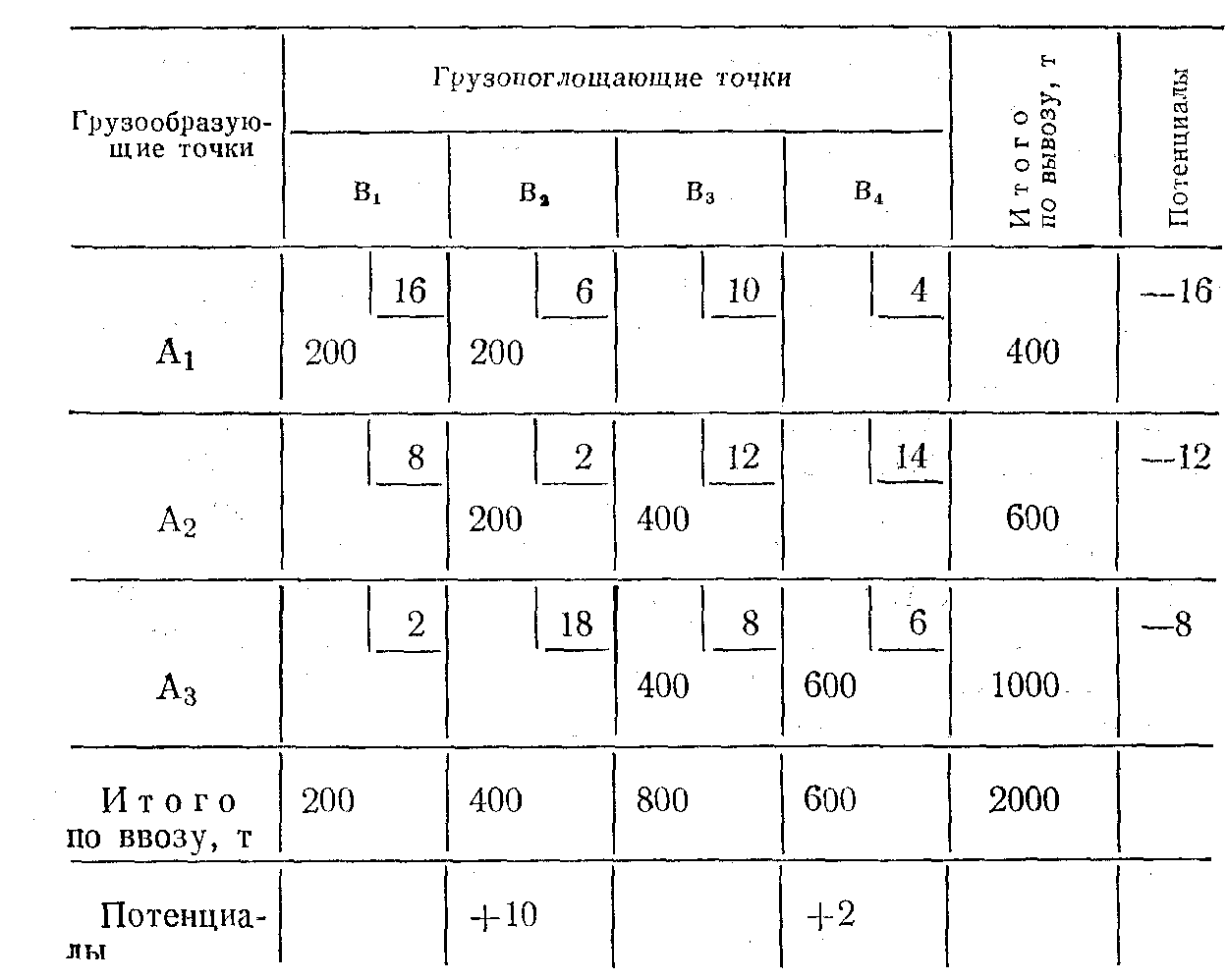
Условимся в дальнейшем называть клетки таблицы, в которых отмечено количество груза, перевозимого от грузоотправителя к данному грузополучателю, загруженными. Количество загруженных клеток всегда должно равняться величине базиса, который будет равен n + т -1 (п- число строк таблицы; т — число столбцов). В нашем примере это условие соблюдено: 3+4 — 1 = 6.

При нашем распределении груза по потребителям первой загруженной клеткой стала левая верхняя клетка А₁В₁ таблицы, остальные загруженные клетки расположились по диагонали, соединяющей левый верхний и правый нижний углы таблицы. Поэтому такой способ первоначального закрепления грузополучателей за грузоотправителями, а следовательно способ первого заполнения таблицы, получил название «диагональный метод» или «метод северо-западного угла».

Полученное таким способом закрепление потребителей груза за грузоотправителями является одним из возможных решений задачи. При этом общая грузовая работа будет равна:

200-16 + 200-6 + 200-2+400- 12 + 400-8 + 600-6 = 16400 т.км.

Однако нельзя сказать, является ли полученный вариант решения оптимальным или нет. Чтобы ответить на этот вопрос, необходимо выполнить следующие действия:

1. Во всех загруженных клетках получают нулевой потенциал.

Для этого по строчкам и столбцам табл. 2 ко всем расстояниям, проставленным в верхних правых углах клеток, прибавляются такие числа (потенциалы), которые в сумме с расстояниями загруженных клеток дают нуль (нулевой потенциал).

Например, чтобы получить в загруженной клетке А₁В₁ нулевой потенциал, нужно ко всем расстояниям строки А₁ прибавить потенциал —16 (16 – 16 = 0).

В загруженной клетке А₁В₂ нулевой потенциал получится в том случае, если к ее расстоянию 6 и ранее прибавленному по строке А₁ потенциалу —16 прибавим по столбцу В₂ потенциал +10 (6 - 16+10 = 0) и т. д.

2. Определяют потенциалы для всех свободных клеток, т. е. находят для каждой свободной клетки сумму указанного в ней расстояния с ранее полученными по загруженным клеткам потенциалами ее строки и столбца.

При решении задачи на минимум оптимальный вариант получается в том случае, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются положительными. величинами.

Если задача решается на максимум, то оптимальным вариант получается тогда, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всем свободных клеток являются отрицательными величинами.

Наличие свободных клеток с отрицательными значениями потенциалов (при решении задачи на минимум) говорит об имеющихся резервах, использовав которые можно получить лучший вариант решения.

В первом варианте решения нашей задачи отрицательные потенциалы имеются в клетках A₁B₄; A₂B₁, А₁В₃ A₃B₁ (табл. 3). Наиболее потенциальной клеткой (клетка, имеющая наибольшее отрицательное значение потенциала) будет клетка А₁В₄, потенциал которой равен — 10.

Во втором шаге решения наиболее потенциальная клетка получает загрузку.

Это вызывает перераспределение загрузки клеток таблицы, которое осуществляется следующим образом.

1. Проверяется, чтобы количество загруженных клеток в предыдущем шаге равнялось п + т = 1.

Если количество загруженных клеток менее, чем п + т = 1, так называемый случай вырождения (см. гл. III), то недостающее число клеток получается путем загрузки соответствующего количества свободных клеток нулями. Клетка, в которой будет проставлена загрузка, равна нулю, считается загруженной.

2. Для наиболее потенциальной клетки А₁В₄ строится контур.

Контуром называется замкнутая ломаная линия, образованная прямыми отрезками, углы соединений между которыми равны 90°.

Строится контур так, чтобы все углы, кроме одного располагались в загруженных клетках, а один угол находился в свободной, наиболее потенциальной клетке.

При соблюдении этих двух правил для каждой свободной клетки можно построить только один контур.

3. Определяются положительные (+) и отрицательные (-) углы контура, считая, что первый положительный угол лежит в свободной клетке, для которой строится контур, рядом с ним находятся отрицательные углы, рядом с отрицательными — положительные и т. д.

Количество положительных углов всегда равно количеству отрицательных углов контура.

Т 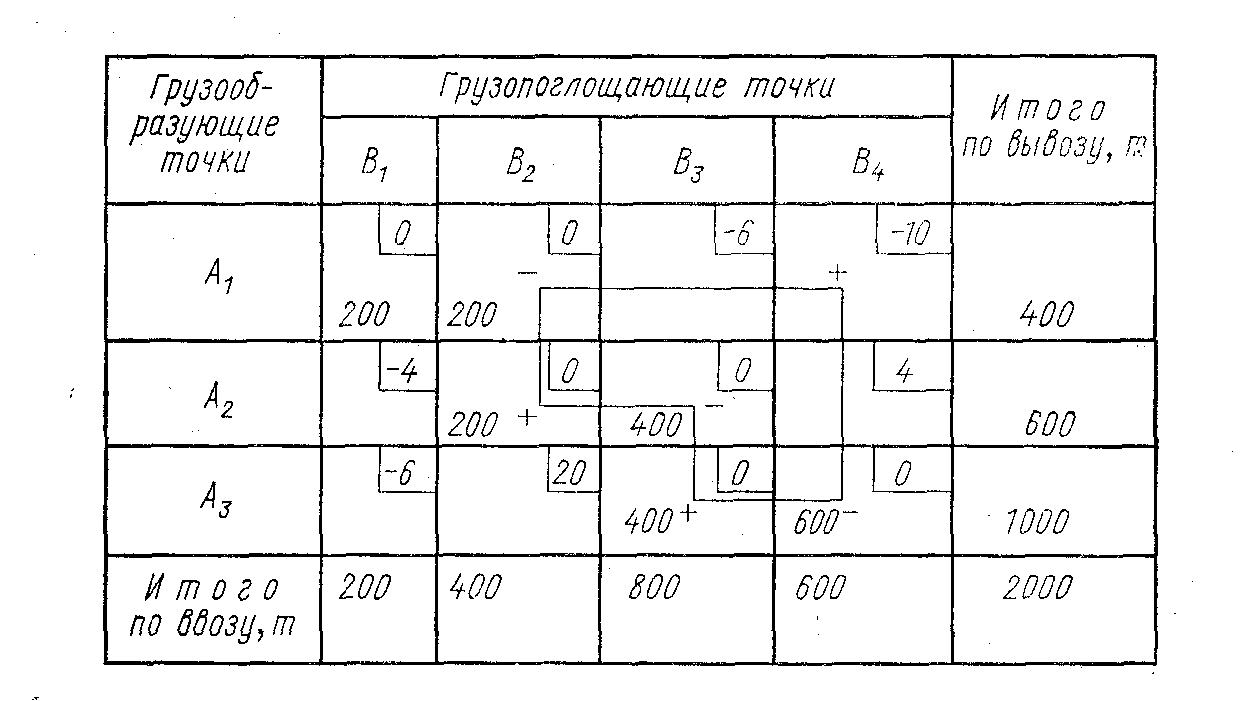аблица 3

4. Выявляется наименее загруженная клетка, занятая отрицательным углом контура. Количество груза, указанное в этой клетке, отнимается из всех клеток, занятых отрицательными углами контура, и прибавляется во все клетки, занятые положительными углами.

В результате такого действия одна или несколько из ранее загруженных клеток становятся свободными, а наиболее потенциальная клетка становится загруженной. Ранее загруженные клетки, которые не оказались расположенными в углах контура, переносятся в таблицу (табл. 4.4) нового варианта закрепления потребителей груза за грузоотправителями без изменений.

В табл. 3 из всех клеток, занятых отрицательными углами контура, наименьшую загрузку имеет клетка А₁В₂—200 т. Эти 200 т вычитаются из всех клеток, занятых отрицательными углами контура, и прибавляются во все клетки, занятые положительными углами. В результате клетка A₁B₂ становится свободной, а наиболее потенциальная клетка А₁В₄ получает загрузку в 200 т.

Загрузка клетки A₁B₁ в которой нет угла контура, в новом варианте решения остается без изменений (см. табл. 4).

Полученный таким путем новый вариант закрепления потребителей за грузоотправителями является возможным решением задачи. При этом варианте решения общая транспортная работа будет равна

200 × 16+200 × 4 + 400 × 2 +200 × 12+600 × 8+400 × 6 = 14 400 т.км.

Это на 2000 т.км меньше, чем получено в первом варианте решения. Величину сокращения грузооборота можно определить и как произведение количества груза, которое получила наиболее потенциальная клетка, на ее потенциал [200 × (-10)]= - 2000 т.км.

Т 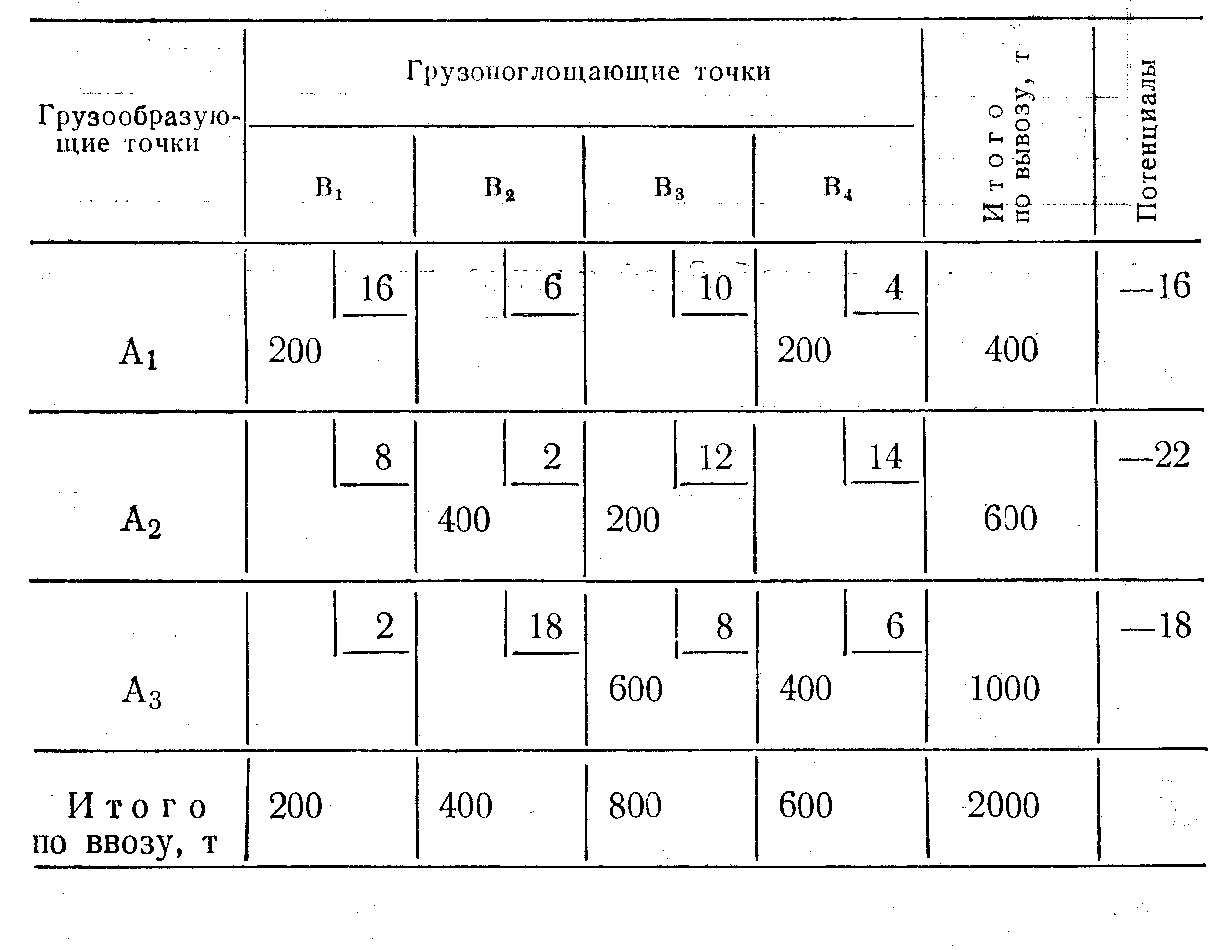аблица 4

+20 +10 +12

Чтобы убедиться, является ли полученный вариант оптимальным, следует повторить все действия, рассмотренные выше, т. е. нужно по новым загруженным клеткам подобрать потенциалы строк и столбцов и определить потенциалы для свободных клеток. Если вариант окажется неоптимальным, то необходимо будет построить контур для новой наиболее потенциальной клетки и найти лучший вариант решения. Задача решается до тех пор, пока не будет найден оптимальный вариант.

Количество промежуточных решений зависит от сложности задачи. В нашем примере оптимальный вариант получен в результате третьего шага решения (табл. 6). Второй же вариант, как и первый, является неоптимальным (табл. 5).

Таблица 5

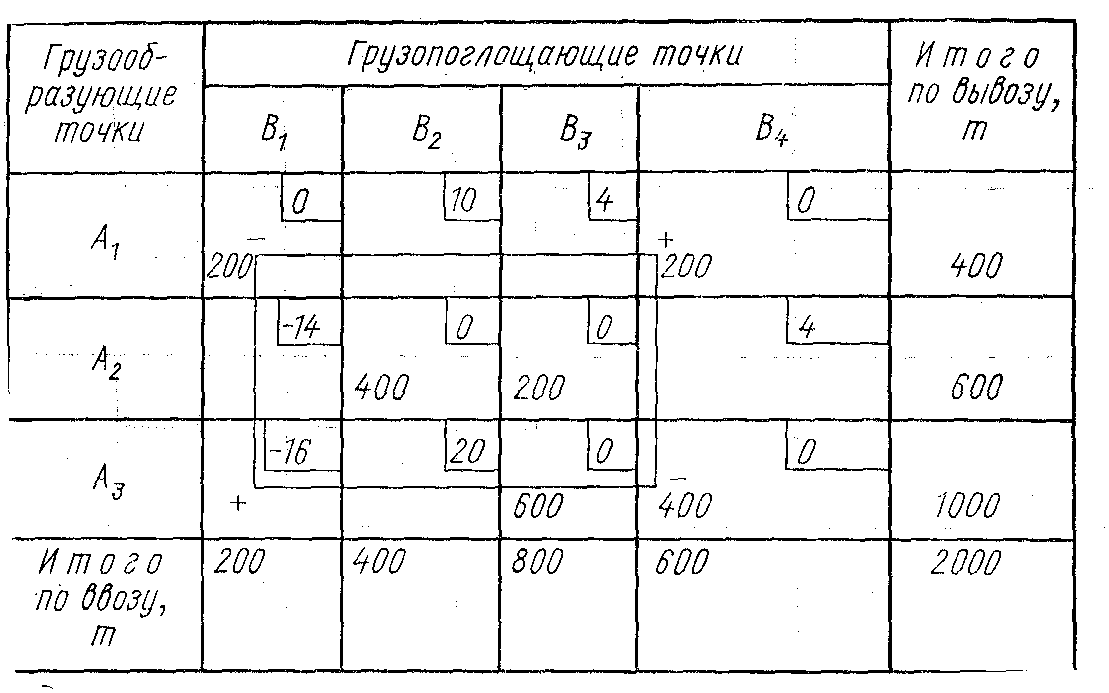
Таблица 6

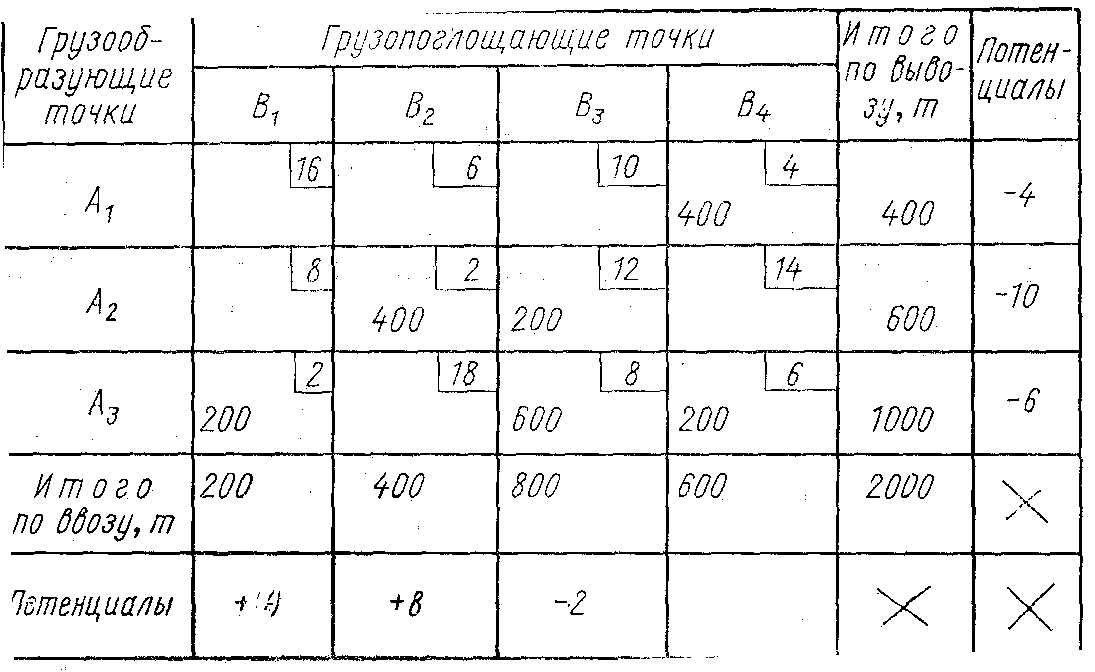
Оптимальность третьего варианта решения подтверждается тем, что во всех свободных клетках таблицы этого варианта потенциалы являются положительными величинами (табл. 7).

Таблица 7

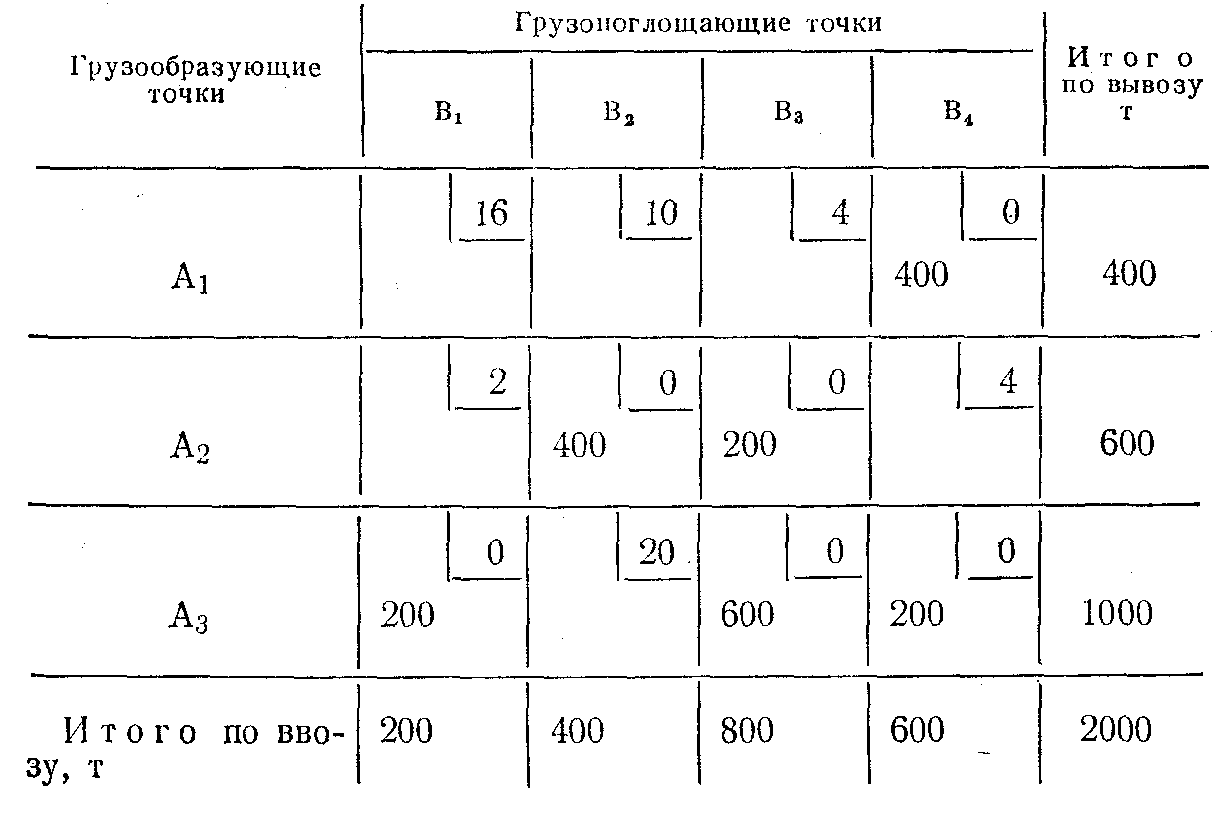
Объем грузовой работы при оптимальном решении будет равен 11 200 ткм.

Второй способ (Метод кредо)

Третий способ (Модифицированный распределительный метод - моди)