Практическое применение теоретических знаний Пример 1-1

Давление в баллоне с кислородом для газовой сварки, расположенного на улице при температуре T₁ = – 10 °С, равно p_l = 10⁷ Па. Каково будет давление при внесении его в помещение при температуре T₂ = – 20 °С?

Ответ: Давление в баллоне будет равно Па.

Пример 1-2

Насколько увеличится давление в системе водяного отопления, если температура теплоносителя увеличилась с 60 до 80 °С. Коэффициент температурного расширения, при давлении 5,9·105 Па и температуре 70 °С, можно принять равным 0,00056 (1/град).

Ответ: Давление в системе водяного отопления увеличится на 225 атмосфер.

Лекция 2. Основы гидростатики, динамики и кинематики жидкости

2.1. Тема 1. Равновесие жидкости

Основные понятия: дифференциальное уравнение равновесия жидкости; три формы записи основного уравнения гидростатики; поверхность равного давления; закон Паскаля; абсолютное, манометрическое и вакуумметрическое давление; сила давления на плоские и криволинейные поверхности; относительный покой жидкости; закон Архимеда; относительный покой жидкости.

Вопросы, на которые необходимо найти ответ в ходе изучения темы:

1. Что обозначает выражение ?

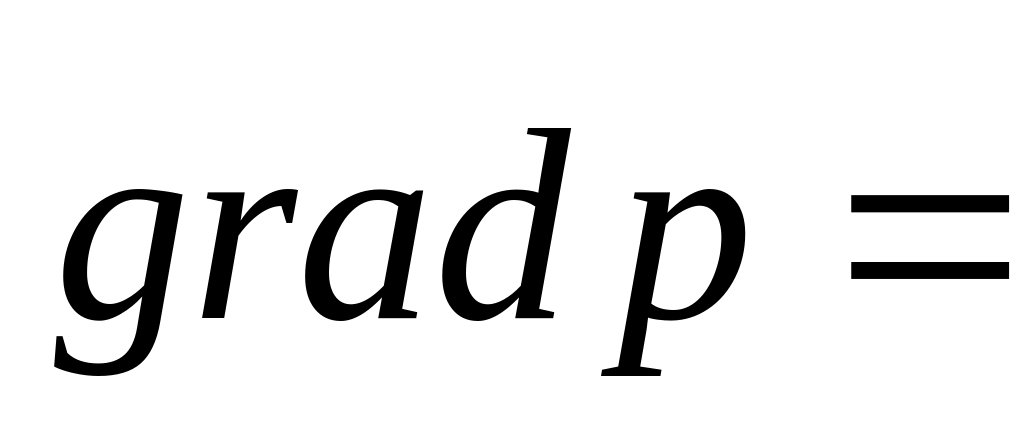
2. Какие выводы можно сделать, если ?

3. Как можно получить основное уравнение гидростатики в дифференциальной форме?

4. В каком случае уравнение Бернулли превращается в основное уравнение гидростатики?

5. Запишите основное уравнение гидростатики в трех его формах. Объясните значение каждого входящего в него слагаемого.

6. Какая плоскость называется плоскостью равного давления?

7. В чем разница между напором и давлением?

8. Что называют удельной энергией положения?

9. Объясните закон Паскаля.

10. Какие механизмы действуют на основе закона Паскаля?

11. Что называют абсолютным давлением, манометрическим давлением, вакуумом?

12. Какое давление будет в напорном потоке, если пьезометрическая линия проходит ниже его геометрической оси?

13. Как определить давление в любой точке жидкости, находящейся в закрытом резервуаре? От чего оно зависит?

14. Чему равна результирующая сила давления на стенки резервуара произвольной формы? Как это доказать?

15. Как определить силу давления жидкости на плоскую горизонтальную поверхность?

16. В чем заключается гидростатический парадокс?

17. Как определить силу давления жидкости на плоскую вертикальную поверхность?

18. Как определить точку приложения результирующей силы давления на плоскую вертикальную поверхность?

19. Как определяется величина силы давления на криволинейные поверхности?

20. Как рассчитать допустимое давление в трубе, чтобы не допустить ее разрыва?

21. Сформулируйте закон Архимеда.

22. Какова природа действия Архимедовой силы?

23. Каковы условия плавания тел, их равновесия?

24. Объясните принцип действия ареометра (прибора для измерения плотности жидкости).

25. Что такое относительный покой жидкости?

26. Какие силы действуют при относительном покое жидкости? Как их записать?

27. Как определить положение свободной поверхности жидкости при ее вращении в цилиндрическом сосуде?

28. Как распределяется давление в любой фиксированной круглоцилиндрической поверхности при относительном покое жидкости?

Практические задачи, решение которых может быть найдено после изучения теоретического материала:

Задача 2.1-1

В сообщающихся сосудах находятся вода и масло. Определить плотность масла, если высота столба воды Н = 150 мм, а разность уровней жидкости в сосудах d = ___мм.

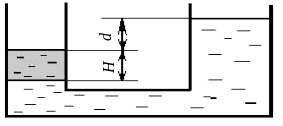
Рис. 2.1. К задаче 2.1-1

Задача 2.1-2

Для измерения высоты налива мазута установлена вертикальная труба. В трубу с малой скоростью подают воздух. Определить высоту Н налива мазута удельным весом  = 8700 Н/м³, если давление воздуха, поступающего в резервуар, эквивалентно высоте ртути в ртутном манометре h_рт = d_н мм (_рт = 13600 кг/м³). Трением при движении воздуха пренебречь.

Рис. 2.2. К задаче 2.1-2

Задача 2.1-3

Для повышения гидростатического давления применяется мультипликатор давления, давление на входе которого = 20 кПа, а диаметры поршней d = d_н мм и D = 400 мм. Определить давление жидкости на выходе из мультипликатора.

Рис. 2.3. К задаче 2.1-3

Задача 2.1-4

Два сообщающихся цилиндра наполнены жидкостью. В меньший цилиндр диаметром d = d_н мм заключен поршень весом G = 100 Н. На какой высоте H установится уровень жидкости в большом цилиндре, диаметром D = 800 мм, когда вся система придет в равновесие? Удельный вес жидкости γ = 9,81 кН/м³. Трением пренебречь.

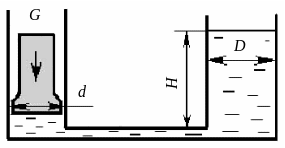
Рис. 2.4. К задаче 2.1-4

Задача 2.1-5

Диаметры поршней дифференциального предохранительного клапана равны D = 2d_н мм и d=d_н мм. Пренебрегая весом поршней и силой трения, определить давление, при котором клапан откроется, если жесткость пружины с = 50 Н/мм, а ее предварительный натяг: x₀ = 12 мм.

Рис. 2.5. К задаче 2.1-5

Примечание. Сила пружины F = с x₀

Задача 2.1-6

Плотность жидкости определяется погружением в нее поплавка. Вес поплавка в воздухе равняется 0,72 кН. Вес поплавка, погруженного в испытуемую жидкость G₁ = 0,54 кН, вес поплавка, погруженного в воду G₂ = 0,56 кН. Определить плотность жидкости.

Задача 2.1-7

Бак водонапорной башни сварен из стальных полос высотой. Определить необходимую толщину стенки нижней полосы, если допускаемое напряжение на разрыв [s] = 1×10⁸ Па, диаметр бака D = 100d_н м, глубина воды в баке Н = 10 м.

Задача 2.1-8

Круглое отверстие в дне резервуара с жидкостью закрыто пластмассовым шариком, вес которого G = 2,45 Н и радиус r = 0,1 м. Диаметр отверстия d = d_н мм. Определить давление р, действующее на шар снизу, при котором отверстие откроется, если глубина воды Н = 2 м.

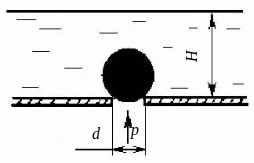
Рис. 2.6. К задаче 2.1-8

Задача 2.1-9

Плотность жидкости измеряется при помощи ареометра. Размеры аэрометра: d = d_н мм, D = 1,5d_н мм, Н = 100 мм, h = 50 мм, масса m = 0,054 кг. Определить плотность жидкости.

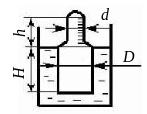
Рис. 2.7. К задаче 2.1-9

Задача 2.1-10

Определить абсолютное давление на поверхности жидкости в сосуде и высоту h, если атмосферное давление равняется 740 мм.рт.ст. Поддерживающая сила F = 10 H, вес сосуда G = 2 Н, его диаметр d = d_н мм. Толщиной стенки сосуда пренебречь.

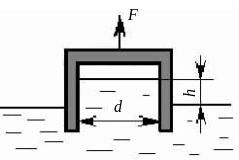
Рис. 2.8. К задаче 2.1-10