4.11. Истечение из насадков

Насадком называется короткая труба длиной от 3 до 5 его диаметров, присоединенная к отверстию. При расчете насадков потерями напора по длине обычно пренебрегают.

Рассмотрим процесс истечения жидкости на примере внешнего цилиндрического насадка (см. рис. 4.23). На входе в насадок образуется водоворотная зона, которая является источником потерь напора, поэтому коэффициент скорости насадка меньше, чем круглого отверстия.

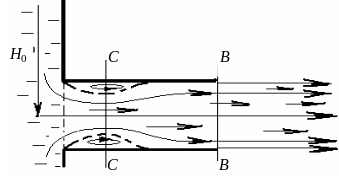
Рис. 4.23. Истечение жидкости из насадка

После сжатия в сечении С-С струя расширяется до сечения насадка и из насадка выходит полным сечением. В сжатом сечении С-С скорость потока выше, чем на выходе, а значит, давление в этом сечении меньше, чем при истечении из отверстия, когда давление равно атмосферному. Таким образом, в насадке создается вакуум и эффект «подсасывания», что увеличивает расход через насадок. Если резервуар открыт, а истечение происходит в атмосферу, то расход можно определить по той же формуле, что и для отверстия.

,

где μ – коэффициент расхода насадка; – площадь сечения насадка.

Истечение через насадок, при котором струя полностью заполняет все пространство насадка, называется истечением без отрыва.

Найдем минимальное давление внутри насадка. Истечение происходит в воздух с давлением Давление на свободной поверхности жидкости – . Расчетный напор – . В сжатом сечении струи < . Разность давления – растет пропорционально напору Н, т. к. скорость в сжатом сечении увеличивается с увеличением Н. Составив уравнение Бернулли для сечений В-В и С-С, можно доказать, что максимальное значение вакуума для воды наступает при . При некотором значении Н, которое называется критическим, давление внутри насадка становится равным 0. Т.к. при дальнейшем увеличении напора давление не может уменьшаться далее, то происходит отрыв струи от стенок из-за того, что наружный воздух прорывается внутрь насадка, и насадок начинает работать как отверстие в тонкой стенке. Такое истечение называется истечением с отрывом.

При истечении с отрывом расход насадка резко уменьшается, т.к. исчезает эффект «подсасывания».

4.12. Виды насадков

Другие виды насадков применяются для того, чтобы увеличить скорость вытекающей струи или расход (см. рис. 4.24).

Конический сходящийся насадок применяется для увеличения скорости истечения струи, ее кинетической энергии. Коэффициенты истечения насадка зависят от угла сужения. При угле сужения β = 14º, μ = φ = 0,95.

Конический расходящийся насадок применяется для увеличения расхода жидкости, т.к. отверстие на выходе из насадка больше, чем на входе. Коэффициенты истечения насадка также зависят от угла расширения. При угле расширения α = 6º, μ = φ = 0,47. Эти насадки работают при небольших напорах, т.к. при увеличении напора больше 3 м может быть отрыв струи от стенок насадка.

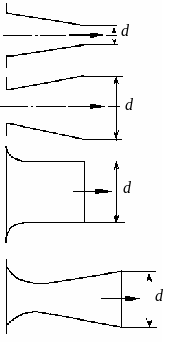
Рис. 4.24. Виды насадков

В коноидальном насадке вход изготавливается по форме естественно сжимаемой струи, что обеспечивает уменьшение зоны отрыва и уменьшение сопротивления насадка. Коэффициент расхода μ = φ = 0,98.

Комбинированный насадок представляет собой комбинацию коноидального и конического расходящегося насадка. Давление в насадке искусственно снижается, что увеличивает расход через насадок. Использовать такой насадок можно лишь при небольших напорах от 1 до 4 метров, т.к. при больших напорах в насадке возникает кавитация, в результате чего увеличивается сопротивление насадка. Длительная кавитация приводит к разрушению насадка.