4.7. Зависимость коэффициентов местных сопротивлений от числа Рейнольдса. Эквивалентная длина

Приведенные данные о коэффициентах местных сопротивлений относятся к турбулентному режиму движения с большими числами Рейнольдса, где влияние молекулярной вязкости проявляет себя незначительно. При ламинарном или близком к нему течении коэффициенты местных сопротивлений зависят от числа Рейнольдса (см. рис. 4.19). При малых значениях Re эффект сопротивления вызван силами вязкости и пропорционален первой степени скорости. Коэффициент сопротивления в этом случае изменяется обратно пропорционально числу Рейнольдса, т.е. , где А – постоянная, зависящая от вида местного сопротивления.

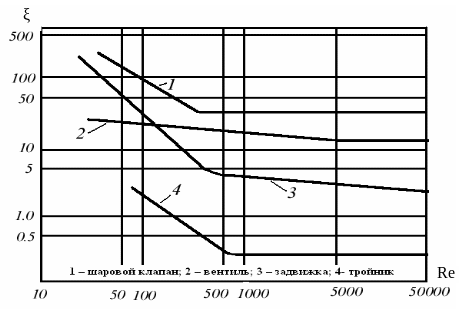
Рис. 4.19. Графики и зависимости коэффициента сопротивления от числа Рейнольдса

При достаточно больших числах Рейнольдса формируются отрывные течения, которые и являются основной причиной местных сопротивлений при больших значениях Re. В этом случае . В первом приближении можно сказать, что при резких переходах в местных сопротивлениях коэффициент ξ не зависит от Re при Re > 3000, а при плавных очертаниях – при Re > 10000.

В общем виде для коэффициента ξ можно записать

,

где – коэффициент сопротивления при больших числах Re, когда ξ = const. В случае линейного закона сопротивления (наклонная прямая на графике) потери напора можно определить по эквивалентной длине.

Эквивалентная длина – такая длина прямого участка трубопровода данного диаметра, на которой потери на трение по длине эквивалентны потери напора, вызываемой данным местным сопротивлением, т.е. . Таким образом, для определения потери напора на местном сопротивлении, мы мысленно заменяем местное сопротивление прямой трубой эквивалентной длины. Это позволяет нам применить формулу Дарси-Вейсбаха для определения потерь напора на местном сопротивлении и учесть изменение числа Re.

,

(4.19)

где – эквивалентная длина, приводится в справочниках, зависит от диаметра трубопровода и вида сопротивления.

4.8. Кавитация

На участках многих местных сопротивлений скорости потока резко возрастают, в результате чего давление уменьшается. Если давление становится ниже давления насыщенных паров жидкости, возникает кавитация. Источником кавитации являются пузырьки газа и пара, которые выделяются в сечении с пониженным давлением. Попадая в сечение с нормальным давлением, пузырьки мгновенно исчезают под действием повышенного давления. В месте исчезновения пузырьков давление резко увеличивается, повышается температура. Кавитация неблагоприятно отражается на работе оборудования, т.к. возникает вибрация, шум, эрозия металла. Кавитационные свойства местных сопротивлений оцениваются по критическому значению числа кавитации.

,

где – давление насыщенных паров жидкости.

Значение чикла кавитации для различных видов местных сопротивлений определяется экспериментально и приводится в справочниках. Предельно допустимая скорость в трубопроводе перед местным сопротивлением определяют по формуле

.

(4.20)

Для проверочного гидравлического расчета трубопровода на бескавитационную работу необходимо, чтобы выполнялось условие .
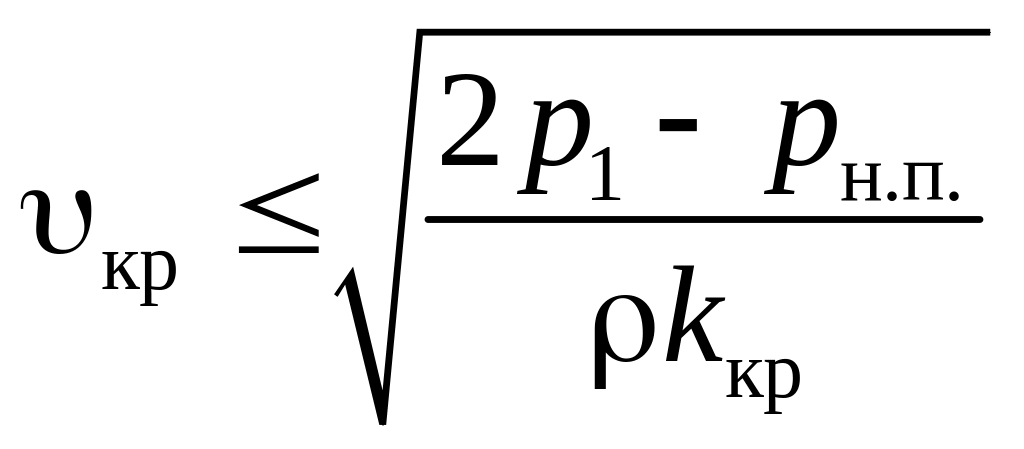