4.3. Формула Дарси-Вейсбаха

Заменим в полученной формуле

и .

Получаем формулу Пуазейля . Перепишем формулу Пуазейля следующим образом , умножим и разделим на

, .

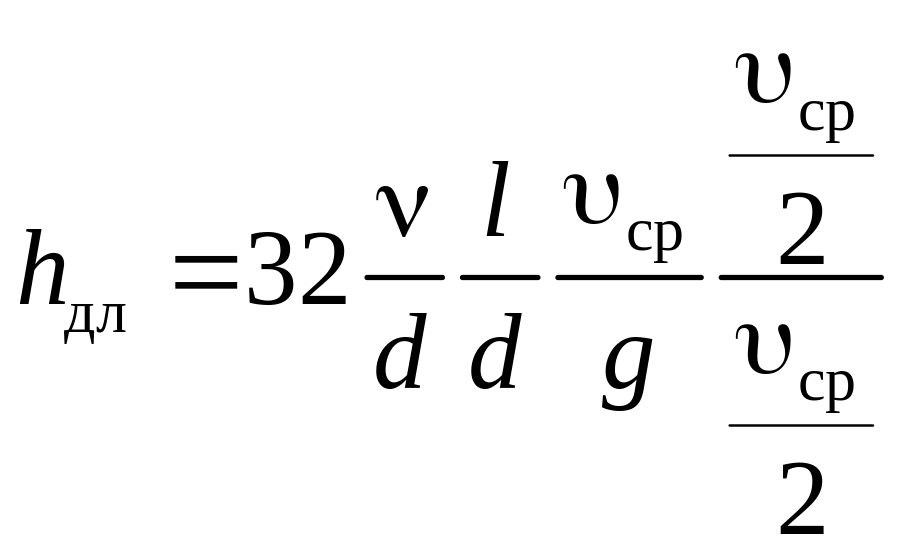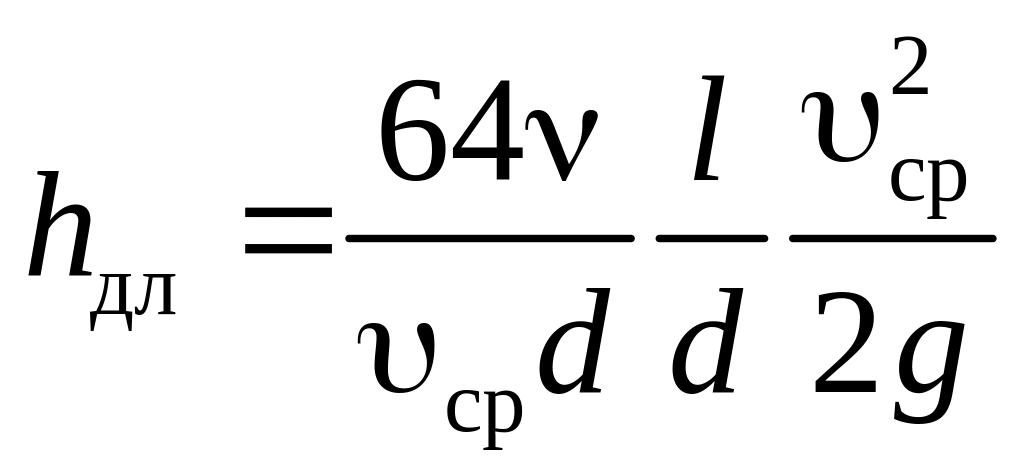Если , то получаем .

Если принять – коэффициент гидравлического трения, то получаем формулу Дарси-Вейсбаха для определения потерь напора по длине

.

(4.8)

4.4. Турбулентное движение в гидравлически гладких и шероховатых трубах

Для ламинарного течения многочисленные экспериментальные исследования подтвердили справедливость вывода о том, что потери напора на гидравлические сопротивления зависят только от величины скорости движения потока в первой степени. Соответственно, гидравлический коэффициент трения

.

(4.9)

Опыты, прежде всего Г.А. Мурина с техническими трубопроводами, показали, что для турбулентного режима λ изменяется не только с изменением числа Re, но на величину λ влияет также техническое состояние трубы. Мурин исследовал 49 труб из различных материалов, бывших в эксплуатации, с различными диаметрами, при различных скоростях движения жидкости. Результаты опытов были получены в виде нескольких кривых (см. рис. 4.11).

Здесь четко различаются три области сопротивления при турбулентном режиме. Линия I соответствует области гидравлически гладких труб, когда величина λ зависит только от числа Re и не зависит от материала трубы. Математическая обработка данных показывает, что для этой области закономерна зависимость

.

(4.10)

Эту зависимость можно использовать в диапазоне чисел Re .

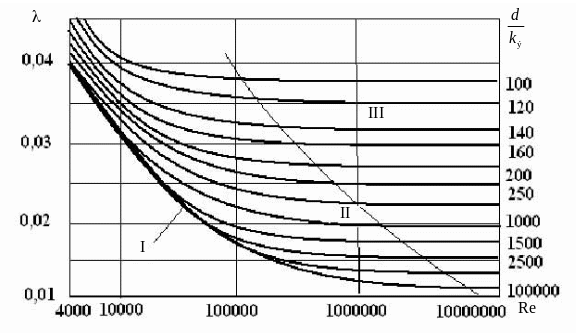
Рис. 4.11. График Мурина

Область II на графике является переходной областью от гидравлически гладких к шероховатым трубам. Величина λ зависит как от числа Re, так и от . Для определения λ в этой области лучше всего подходит формула Альтшуля

.

(4.11)

Эту формулу можно использовать в диапазоне чисел .

Область III является областью гидравлически шероховатых труб. На графике в этой области кривые зависимости λ от Re параллельны между собой, т.е. λ не зависит от числа Re, а определяется только величиной . В этой области λ определяется по формуле

,

(4.12)

которую можно использовать при .

Анализ возможных значений коэффициентов гидравлического трения для различных условий показывает, что трубопроводы для систем теплогазоснабжения и вентиляции работают преимущественно в переходной области сопротивления. Водопроводные линии чаще всего относятся к области шероховатых труб. Как гидравлически гладкие работают пластмассовые, алюминиевые, латунные трубы.

Характер кривых зависимости 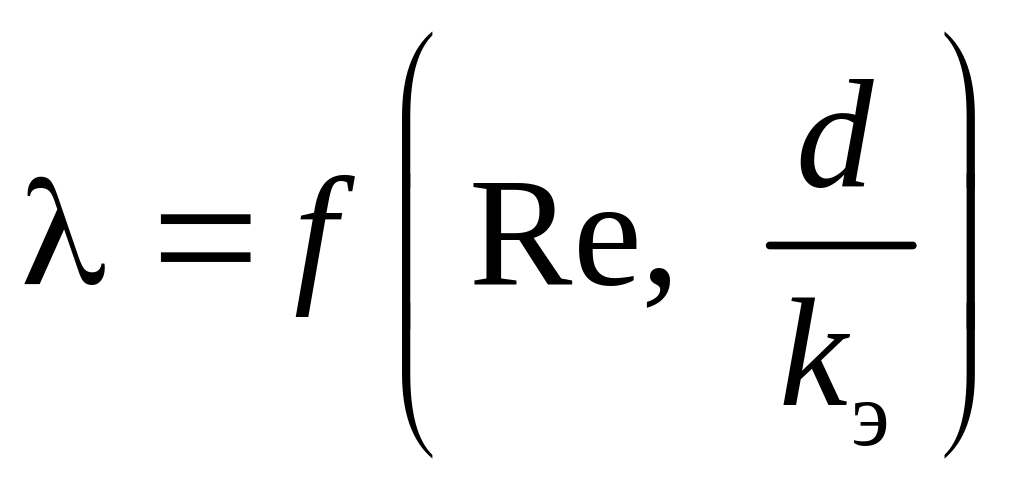определяется характером обтекания потоком жидкости в пристеночном слое выступов шероховатости, которые всегда имеются на поверхности трубы (рис. 4.12).

Рис. 4.12. Движение жидкости в гидравлически гладких и шероховатых трубах

При небольших скоростях движения жидкости частицы обтекают выступы без образования вихрей, что объясняется малыми силами инерции. Такое обтекание потоком выступов характерно для области гидравлически гладких труб. С увеличением скорости движения, силы инерции частиц жидкости возрастают и возникают отдельные вихри за некоторыми выступами шероховатости. Количество вихрей и их величина возрастает с увеличением скорости движения жидкости. Такая картина обтекания характерна для переходной области. При дальнейшем увеличении скорости протекании жидкости, вихри располагаются за всеми выступами, их размер не изменяется, что характерно для области гидравлически шероховатых труб. Размер вихрей зависит, как мы видим, от размера выступов шероховатостей, их формы, частоты их распределения по поверхности.

В качестве интегральной характеристики состояние внутренней поверхности трубы используется эквивалентная шероховатость , которая определяется экспериментально на основе гидравлических испытаний различных трубопроводов и приводится в справочниках. Приведем некоторые значения для труб из различных материалов:

Таблица 3-1

Материал и состояние трубы	, мм
Из цветных металлов и стекла	0,001
Стальные бесшовные: – новые – бывшие в эксплуатации	0,014 0,2
Стальные сварные: – новые – бывшие в эксплуатации	0,05 0,5

Порядок определения потерь напора по длине

1. Определяем число Re.

2. Определяем режим движения.

При ламинарном режиме:

3. Определяем λ.

4. Подсчитываем .

При турбулентном режиме:

3. Находим в справочнике .

4. По значениям и Re определяем область сопротивления

5. По соответствующей формуле определяем λ.

6. Подсчитываем .