4.1. Виды гидравлических сопротивлений

Получение конкретных зависимостей для расчета потерь энергии при движении жидкости в трубках и каналах является основным содержанием внутренней задачи гидравлики.

Различают два вида сопротивлений отличающиеся одно от другого по свое структуре: сопротивление по длине и местные сопротивления.

Потери по длине. Рассмотрим движение жидкости в горизонтальном трубопроводе постоянного сечения с неизменной эпюрой скоростей, т.е. равномерное движение. Запишем для двух сечений уравнение Бернулли в форме давлений

.

Здесь: = , = , тогда уравнение Бернулли можно записать в следующем виде: , где – давление, теряемое на преодоление сил трения.

Вывод: Работа сил давления расходуется на преодоление сил трения, что и обуславливает потери механической энергии, которые прямо пропорциональны длине пути движения.

В зависимости от формы записи уравнения Бернулли эти потери называются:

• потерями давления по длине ;

• потерями удельной энергии по длине ;

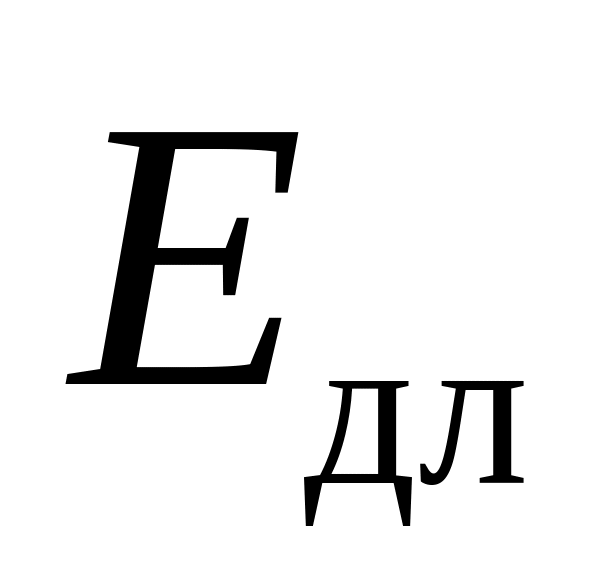• потерями напора по длине .

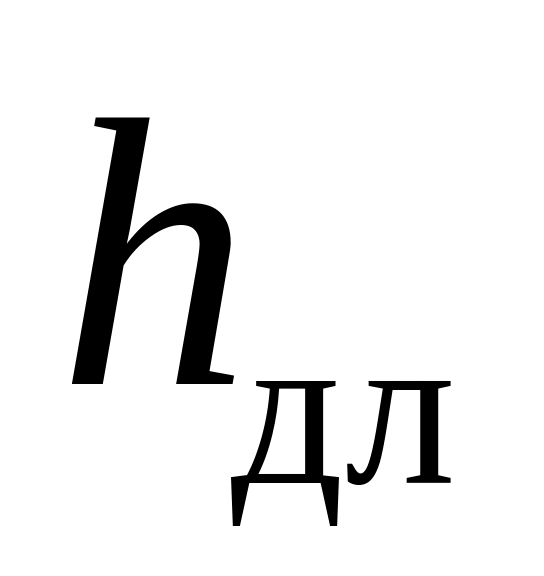Местные потери образуются в результате изменения структуры потока по пути движения жидкости.

Рассмотрим движение жидкости через частично открытую задвижку в трубопроводе (см. рис. 4.9).

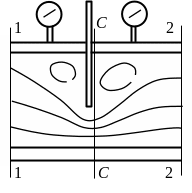
Рис. 4.9. Задвижка

В отверстии (сечение С-С) скорости увеличиваются, а давление уменьшается. В сечении 2-2, на некотором расстоянии после задвижки, скорости принимают значения, равные скоростям в сечении 1-1 перед задвижкой.

На участках 1-С и С-2 наряду с основным течением возникает область вихревого движения. Скорости движения частиц в этой зоне значительно меньше, чем в основном потоке, что обуславливает возникновение больших напряжений трения из-за большого градиента скорости. Более подробно о местных гидравлических сопротивлениях будет рассмотрено далее. В зависимости от формы записи местные потери записываются как или .

Общие потери в трубопроводе складываются из потерь по длине и потерь на местных сопротивлениях + .

4.2 Сопротивление по длине при движении в цилиндрической трубе при ламинарном течении

При ламинарном режиме жидкость движется концентрическими слоями. Воспользуемся формулой Ньютона для напряжений трения, приняв

.

Знак «минус» указывает на то, что скорость уменьшается в направлении оси r (от центра к стенке трубы).

Составим уравнение равномерного движения жидкости для выделенного объема длиной l и радиусом r (см. рис 4.10).

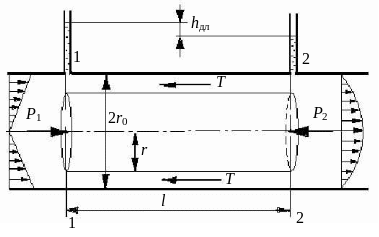
Рис.4.10. Движение жидкости в прямой трубе

На выделенный объем действуют внешние силы: нормальные к живым сечениям: силы давления , и касательные силы сопротивления Т, приложенные к боковой поверхности

Уравнение равновесия этих сил относительно направления движения:

или ,

или .

(4.1)

Вывод: При ламинарном движении в круглой трубе напряжение трения максимально у стенки и равно 0 на оси трубы (см. рисунок).

Закон распределения скоростей по сечению трубы можно получить из следующего уравнения

,

.

После интегрирования, получаем: .

Константу находим из граничных условий: , .

откуда ,

.

Окончательно получаем

.

(4.2)

Вывод: При ламинарном течении скорости в сечении трубки распределяются по параболическому закону (см. рис. 4.10).

Максимальная скорость на оси трубы будет при r = 0

, или .

(4.3)

Определим величину расхода жидкости через определенное сечение.

Расход элементарной струйки , где dS – площадь сечения трубки тока,

.

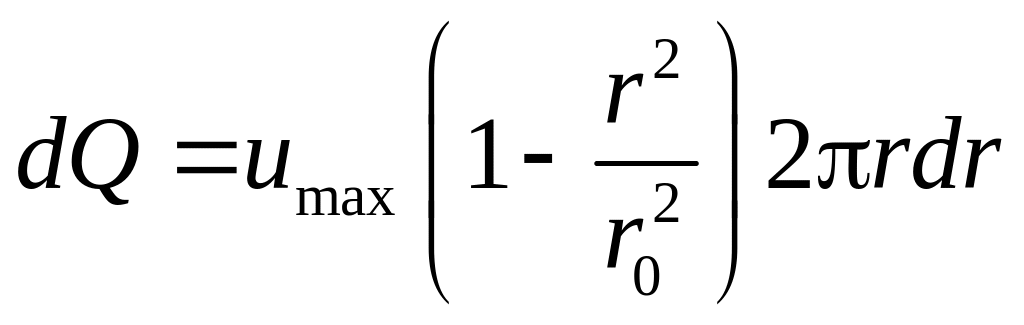Полный расход

.

(4.4)

Вывод: Для того чтобы определить расход при ламинарном режиме достаточно измерить скорость на оси потока и умножить ее на половину площади живого сечения.

Определим среднюю скорость. Согласно определению .

, .

Получаем

.

(4.5)

Вывод: Средняя скорость при ламинарном режиме в два раза меньше скорости на оси потока.

Коэффициент Кориолиса вычисляется из выражения .

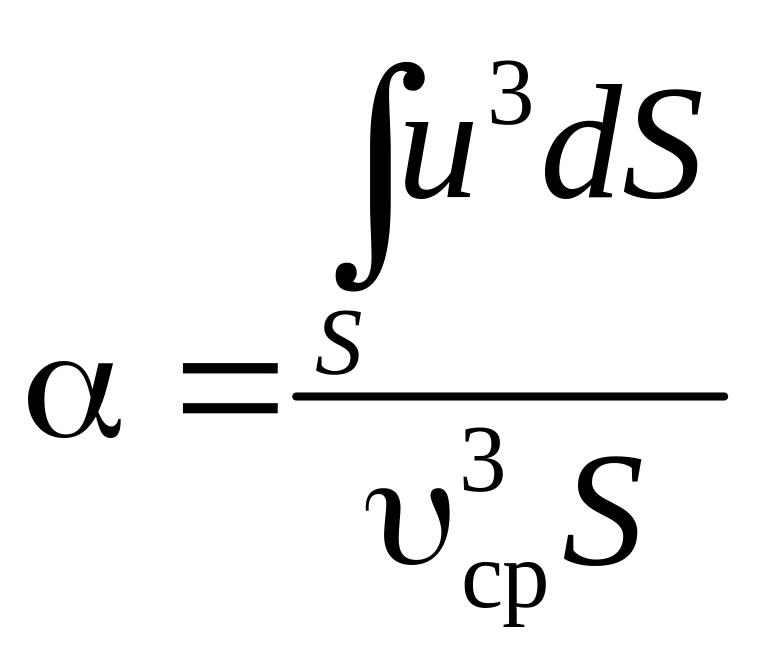Подставляем значения u и dS, интегрируя, получаем

.

(4.6)

Для получения закона сопротивления при ламинарном режиме вернемся к формуле расхода .

Подставим значение .

, откуда .

Разделим на ρg, в результате получаем

,

где – потери давления; – потери напора.

Получаем

.

(4.7)

Вывод: Потери напора на преодоление сил сопротивления по длине при ламинарном режиме прямопропорциональны расходу и длине трубопровода и обратнопропорциональны радиусу трубы в четверной степени.
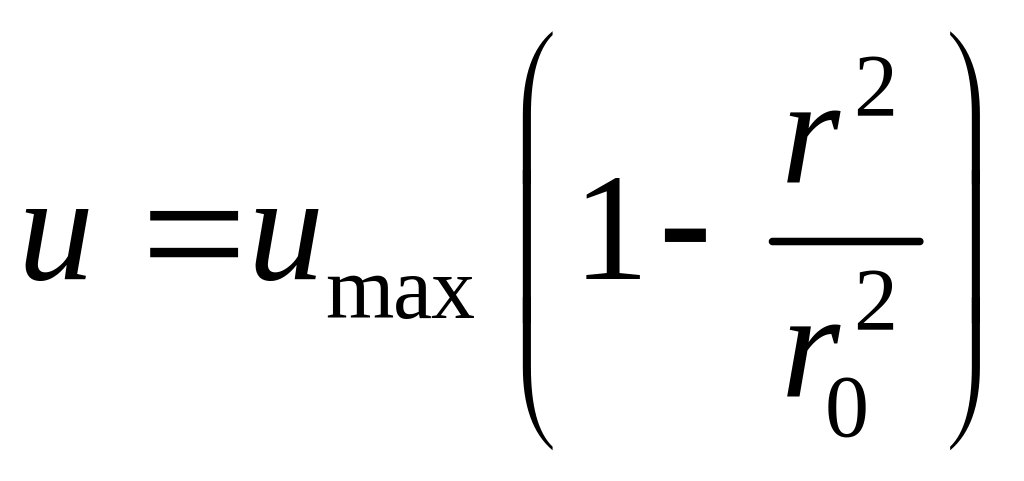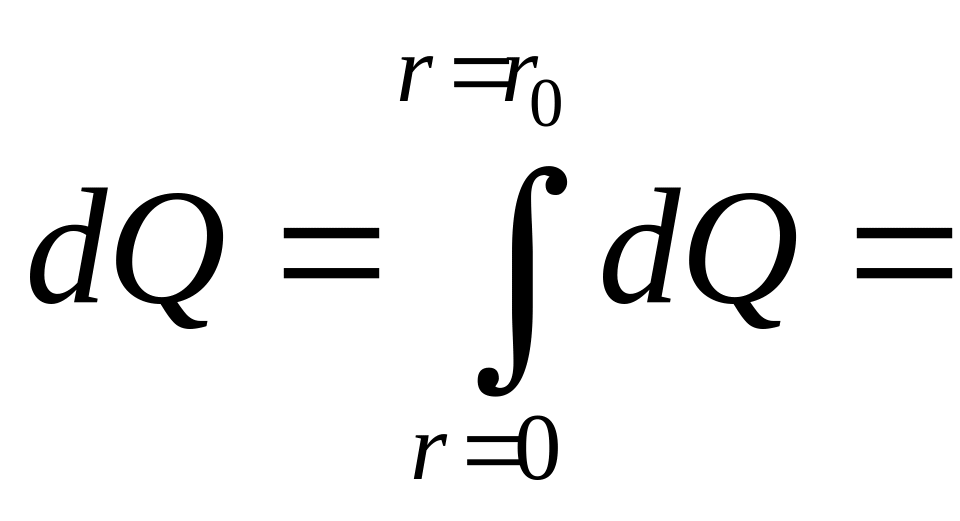
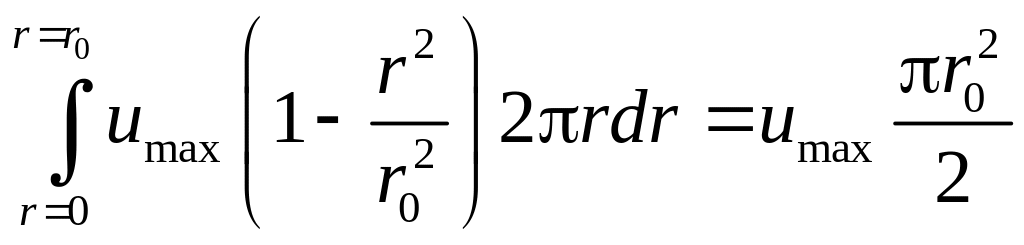