6. Расходомер Вентури.

Расходомер (см. рис. 3.7) служит для измерения расхода жидкости и представляет собой плавную сходящуюся – расходящуюся вставку, к которой подключается дифферциальный манометр. Для вывода расчетной формулы применим уравнение Бернулли для сечения 1-1 перед сужением и сечения 2-2 в сужении (α₁ = α₂ = 1).

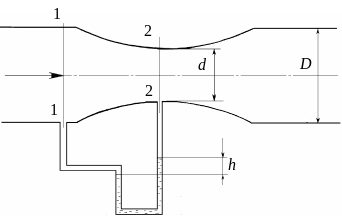
Рис. 3.7. Расходомер Вентури

.

(3.18)

С учетом уравнения неразрывности

.

(3.19)

Откуда , .

Зная перепад давления по дифференциальному манометру, можно для данного диаметра вставки и трубы определить расход жидкости, протекающей через трубу.

Для ртутного манометра

Обычно расходомеры выпускаются для определенных диаметров труб и его диаметр d и D известны.

В этом случае формула упрощается

,

(3.20)

где μ – коэффициент, учитывающий конструктивные особенности прибора, в частности , и вносится в паспорт прибора.

7. Ротаметры.

Ротаметры (см. рис. 3.8) используются для измерения расхода жидкостей, имеющих слабые коррозийные свойства. Ротаметр состоит из сужающейся стеклянной трубки и металлического конусообразного измерителя. На измеритель действуют следующие силы: сила тяжести G, архимедова сила F_A, сила динамического давления жидкости F. Для измерителя, находящегося в покое, можно записать

или ,

(3.21)

где ρ – плотность жидкости; V – объем измерителя;  – скорость течения жидкости; S – площадь сечения измерителя.

Сила тяжести и архимедова сила – величины постоянные, поэтому сила динамического давления жидкости при любом расходе будет также постоянной.

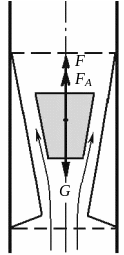
Рис. 3.8. Ротаметр

При уменьшении расхода измеритель опускается, уменьшается сечение для прохождения жидкости, соответственно скорость увеличивается, сохраняя постоянным значение силы динамического давления. Если мы проградуируем стеклянную поверхность ротаметра в единицах измерения расхода, то в зависимости от высоты поднятия измерителя можно определять расход.

Лекция 4. Гидравлические сопротивления

Основные понятия: гидравлические сопротивления; сопротивление по длине; местные сопротивления; коэффициент гидравлического трения; коэффициент эквивалентной шероховатости; график Мурина; гидравлически гладкие и шероховатые трубы; движение жидкости в трубах некруглого сечения; эквивалентная длина; кавитация; истечение жидкости в атмосферу; отверстие в тонкой стенке; насадки; коэффициенты истечения; критическое истечение; истечение при переменном напоре; истечение под уровень.

Вопросы, на которые необходимо найти ответ в ходе изучения темы:

1. Чем сопротивление по длине отличается от местного сопротивления?

2. Что называют общими потерями?

3. Привести примеры сопротивлений по длине и местных сопротивлений.

4. Почему происходит уменьшение давление при движении жидкости в трубе? Докажите.

5. Когда применяется формула Дарси-Вейсбаха?

6. От каких параметров зависит величина потерь напора по длине при ламинарном режиме?

7. Напишите уравнение равновесия сил, действующих на выделенный цилиндрический объем жидкости, движущийся равномерно.

8. Как распределяется напряжение трения в трубе при ламинарном режиме? Докажите.

9. Как распределяются скорости в трубе при ламинарном режиме? Как это доказать?

10. Как построить эпюру скорости, если известна величина скорости на оси потока?

11. Как можно определить расход при ламинарном движении жидкости?

12. Как из формулы Пуазейля получить формулу Дарси-Вейсбаха?

13. От чего зависит коэффициент гидравлического трения при ламинарном режиме?

14. От каких факторов зависит коэффициент гидравлического трения при турбулентном течении в трубах?

15. Как выглядит график Мурина? Какие выводы можно сделать из этого графика?

16. Что называют коэффициентом эквивалентной шероховатости?

17. Чем гидравлически гладкие трубы отличаются от гидравлически шероховатых?

18. Сколько зон сопротивления имеется при турбулентном движении? Как это доказать?

19. Почему область шероховатого трения часто называют областью квадратичного сопротивления?

20. Каков порядок определения потерь напора по длине?

21. Каковы особенности определения потерь в трубопроводах некруглого сечения?

22. Что называют гидравлическим радиусом?

23. Что называется простым трубопроводом?

24. Почему при расчете длинных трубопроводов пренебрегают потерями на местных сопротивлениях?

25. Как определяют потери напора по длине в длинных трубопроводах?

26. Что называют модулем расхода?

27. Что называют требуемым напором, как его определить?

28. Как определить величину статического напора?

29. В чем отличие расчета трубопроводов при их параллельном и последовательном соединении?

30. Каковы особенности расчета трубопроводов при непрерывной раздаче расхода по пути?

31. Какова особенность расчета разветвления?

32. Почему возникает гидравлический удар в трубопроводах?

33. От чего зависит повышение давления при гидравлическом ударе?

34. От каких параметров зависит скорость распространения гидравлического удара?

35. Чем прямой гидравлический удар отличается от непрямого?

36. Как рассчитать повышение давления при прямом и непрямом гидравлическом ударе?

37. Как рассчитать время закрытия задвижки в магистральном трубопроводе?

38. Каков принцип действия гидравлического тарана?

39. Как избежать гидравлический удар в водопроводных сетях внутри здания?

40. От чего зависят потери напора на местных сопротивлениях?

41. Почему коэффициенты местных сопротивлений определяется почти всегда экспериментально?

42. Что называют эквивалентной длиной?

43. Когда для определения потерь напора на местном сопротивлении используется эквивалентная длина?

44. Каковы причины возникновения потерь напора при резком расширении и сужении трубы?

45. В каком случае коэффициент местного сопротивления при постепенном изменении диаметра трубы будет минимальным?

46. От каких факторов зависит коэффициент местного сопротивления при плавном повороте трубы?

47. От чего зависит коэффициент местного сопротивления вентиля?

48. Что влияет на характер изменения коэффициента местного сопротивления от числа Re?

49. Как определить потери напора на местных сопротивлениях при ламинарном режиме?

50. Что называют кавитацией?

51. Как избежать кавитации?

52. Что называют отверстием в тонкой стенке, а что насадком?

53. Как определить скорость струи при истечении через отверстие? Как получена эта формула?

54. Как определить расход при истечении через отверстие?

55. Какие коэффициенты истечения вы знаете, как они связаны между собой?

56. Почему происходит сжатие струи при истечении?

57. Какова зависимость коэффициентов истечения от числа Re? Почему?

58. Почему длина насадка должна быть не менее трех диаметров, но не более пяти?

59. Почему при истечении через насадок расход увеличивается?

60. Почему при напорах воды около 14 м коэффициент расхода цилиндрического насадка резко снижается?

61. Какое истечение через насадок называется безотрывным?

62. Почему расход коноидального насадка больше, чем цилиндрического?

63. Почему не рекомендуется повышать напор воды при истечении через комбинированный насадок более 4 м?

64. В каких случаях, какие насадки применяются?

65. Почему при определении времени истечения из резервуара нельзя применить уравнение Бернулли?

66. При помощи какого метода определяется время истечения из резервуара, если резервуар имеет произвольную форму?

67. Как определить время опорожнения цилиндрического резервуара?

68. Что называют истечением при переменном напоре?

69. От чего зависит расход жидкости при истечении под уровень?

Практические задачи, решение которых может быть найдено после изучения теоретического материала:

Задача 4-1

В закрытом резервуаре поддерживается постоянное манометрическое давление p_м = 0,82 атм, под действием которого по трубе диаметром d₁ = мм и общей длине l = 25 м (расстояние от начала до колена l₁ = 5 м) вытекает жидкость при температуре t. Определить расход при напоре H₁ = 2 м.

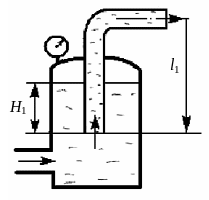
Рис. 4.1. К задаче 4-1

Задача 4-2

Истечение происходит из открытого резервуара при постоянном напоре H₁ = 5 м по короткому трубопроводу переменного поперечного сечения с диаметрами d₁ = мм и d₂ = 100 мм в атмосферу. На втором участке трубопровода имеются два колена с плавным поворотом. Длина первого участка l₁ = 0,8 м, длина второго участка l₂ = 2 м. Определить скорость истечения u₂ и расход Q₂ через трубопровод.

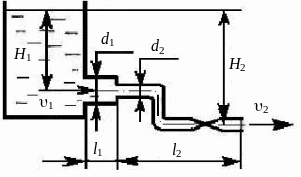
Рис. 4.2. К задаче 4-2

Задача 4-3

Из резервуара А, заполненного жидкостью на высоту H₁ = 5 м и находящегося под манометрическим давлением р_м = 150 кПа, жидкость подается по трубопроводу длиной l = 6 м и диаметром d = мм в резервуар В на высоту Н = 2 м. Определить расход Q и скорость протекающей по трубопроводу жидкости.

Рис. 4.3. К задаче 4-3

Задача 4-4

К закрытому резервуару, на свободной поверхности которого действует манометрическое давление р_м = 500 кПа, подсоединен трубопровод переменного сечения с диаметрами d₁ = мм и d₂ = мм, заканчивающийся соплом диаметром d_c = d₁. Трубопровод подсоединен на глубине Н₁ = 8 м. На первом участке длиной l₁ = 10 м установлен вентиль. Длина второго участка l₂ = 5 м. Определить скорость истечения  и расход Q вытекающей из сопла жидкости при температуре t.

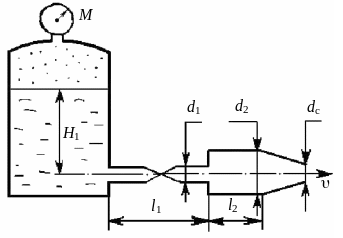
Рис. 4.4. К задаче 4-4

Задача 4-5

Ц

Рис.4.5 к задаче 4-5.

ентробежный насос подает воду с температурой t = 15 °С по трубе диаметром d = мм и длиной l = 27 м. Насос создает давление на выходе р_н = 2,65 атм и подачу Q = 16 л/с. Определить напор H, создаваемый насосом.

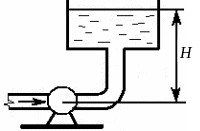
Рис. 4.5. К задаче 4-5

Задача 4-6

Какую высоту h должна иметь воронка для налива жидкости в бочку из цистерны, чтобы мазут не переливался через край при полном открытии крана. Диаметр крана d₁ = мм, напор в цистерне Н = 3 м. Диаметр выходного отверстия воронки d₂ = 2d₁. Длина крана l = 1 м.

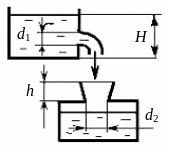
Рис.4.6. К задаче 4-6

Задача 4-7

Призматический резервуар разделен на две части перегородкой. В левом отсеке поддерживается постоянный уровень жидкости. В перегородке имеется круглое отверстие диаметром d₁ = мм, расположенное на глубине Н = 3,2 м. Во внешней стенке расположено отверстие диаметром d₂ = 100 мм. Определить расход Q при Dh = 1,5 м.

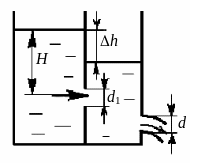
Рис.4.7. К задаче 4-7

Задача 4-8

На поршень, диаметром D = 100 мм действует сила Р = 1 kH. Определить скорость движения поршня при диаметре отверстия d = мм и толщине поршня а = 8 мм.

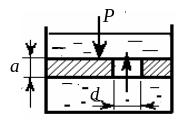
Рис. 4.8. К задаче 4-8

Задача 4-9

В резервуаре находится 1,1 м воды и 6,2 м нефти плотностью 900 кг/м². Диаметр резервуара d = м. Определить время слива воды через короткий патрубок диаметром 100 мм.

Задача 4-10

При исследовании истечения через круглое отверстие диаметром d₀ = мм, получено: диаметр струи d_c = мм, напор Н = 2 м, время заполнения объема V = 10 л t = 32,8 с. Определить коэффициенты истечения m, j, e. Распределение скоростей по сечению струи принять равномерным.
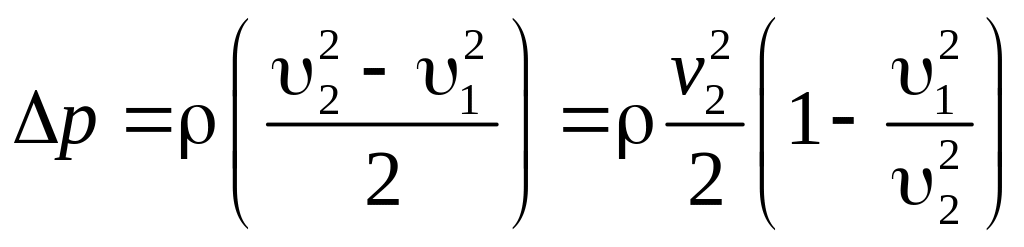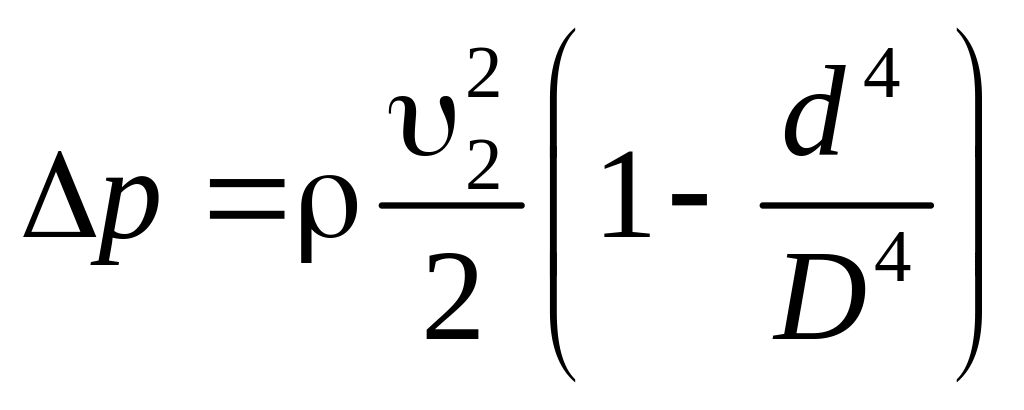