2.2.10. Уравнение Бернулли для элементарной струйки невязкой сжимаемой жидкости
Плотность сжимаемой жидкости изменяется в процессе движения. Проинтегрировав дифференциальное уравнение одномерного движения жидкости для струйки, получаем:
|
|
(2.56) |
.При установившемся движении влияние сжимаемости практически проявляется только в газах, при анализе течения которых удельной энергией положения можно пренебречь. Тогда:
|
|
(2.57) |
.
Это уравнение можно назвать уравнением
Бернулли для сжимаемой жидкости. Член
характеризует
потенциальную энергию газа с учетом
преобразования его внутренней энергии.
Вывод: При установившемся течении невязкого газа сумма удельной потенциальной, внутренней и кинетической энергии есть величина постоянная.
Для вычисления интеграла необходимо знать процесс изменения состояния газа при этом течении. Если считать что течение происходит без теплообмена, то для невязкого газа это будет отвечать изоэнтропическому изменению состояния. Такой процесс описывается уравнением
|
|
(2.58) |
,где k – показатель адиабаты процесса; С – постоянная.
Подставим в интеграл
вместо ρ его значение из предыдущего
уравнения
,
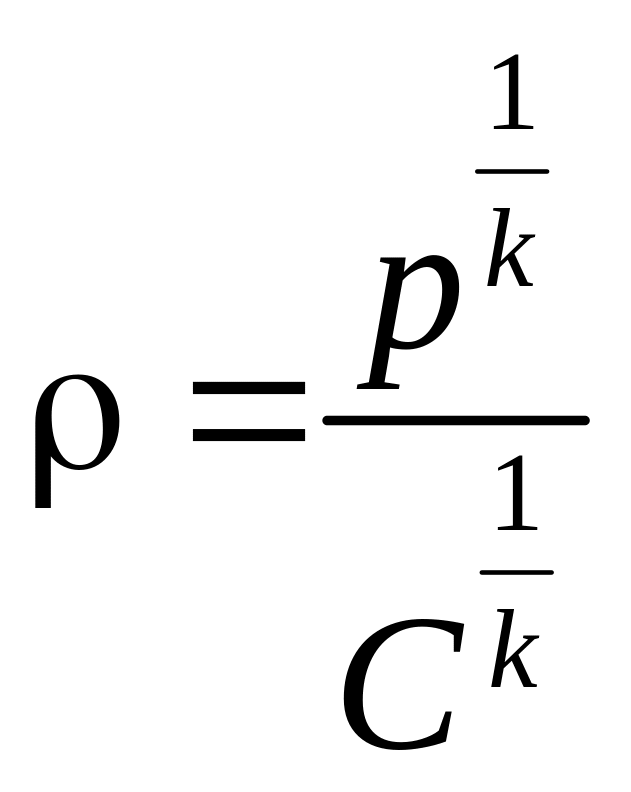тогда
.
Теперь уравнение Бернулли для сжимаемой жидкости принимает вид
.
Поскольку отношение
|
|
(2.59) |
.Из этого уравнения следует, что изменение скорости вдоль трубки тока сжимаемого газа связано с изменением температуры. При увеличении скорости температура падает и наоборот.
2.2.11. Уравнение Бернулли для потока вязкой сжимаемой жидкости
При составлении уравнений движения сжимаемой жидкости следует учитывать, что не только скорости, но и плотности, температуры и давления отдельных струек в пределах живых сечений неодинаковы, что значительно усложняет исследование. Поэтому поток конечных размеров рассматривают как одну струйку. Заменив в уравнении для струйки скорость струйки u на среднюю скорость потока ср, можно сразу написать уравнение Бернулли сжимаемой невязкой жидкости:
|
|
(2.60) |
.Теперь составим уравнение Бернулли для вязкой сжимаемой жидкости, для чего запишем дифференциальное уравнение движения
интегрирование которого для сжимаемой жидкости зависит от конкретных условий движения и закона изменения состояния газа.
При адиабатическом течении, где отсутствует обмен тепла со средой вне границ потока, можно получить уравнение движения в конечном виде, для чего необходимо применить понятие энтальпии
|
|
(2.61) |
где q – количество тепла, передаваемое 1 кг газа.
Подставив уравнение энтальпии в уравнение Бернулли, получим
При адиабатическом течении энергия, потерянная на трение, переходит во внутреннее тепло (dEn = dq), тогда
Проинтегрировав, получим
|
|
(2.62) |
Мы получили основное уравнение адиабатического течения газа.
Вывод: Сумма удельной кинетической энергии и энтальпии остается неизменной в процессе движения газа.
Можно доказать, что для воздуха сжимаемостью можно пренебречь, если скорость течения не превышает 70 м/с, для природного газа – 90 м/с. В системах вентиляции и газопроводов низкого давления скорости течения не превышают указанных пределов, поэтому расчет в этих системах ведется как для несжимаемой жидкости. В этих системах расчет можно вести по уравнению Бернулли в форме давлений
.