2.2.3. Виды движения жидкости

Все случаи течения жидкости можно разделить на виды, представленные на рисунке 2.36.

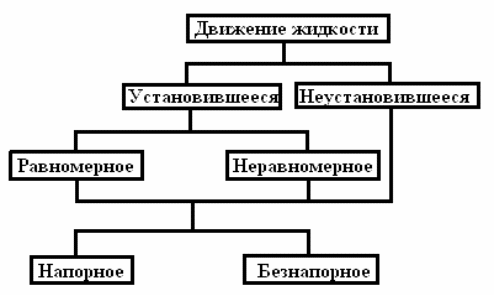
Рис. 2.36. Виды движения жидкости

Установившееся движение жидкости – движение жидкости, при котором все параметры жидкости (давление, температура, скорость и др.) не изменяются по времени.

.

(2.37)

Для неустановившегося движения:

.

(2.38)

Равномерное движение – установившееся движение, при котором скорость по всей длине потока не изменяется:

.

(2.39)

Напорное движение устанавливается в закрытых гидравлических системах, в которых жидкость течет в, основном, под действием силы давления, безнапорное движение наблюдается в открытых системах, в которых движение жидкости происходит под действием силы тяжести.

2.2.4. Интегральная формула количества движения

В теоретической механике изучается теорема о количестве движения материальных точек, которую можно применить в гидравлике. Будем считать движение жидкости в канале (см. рис 2.37) установившемся. Распределение давления в сечениях 1-1 и 2-2 гидростатическое. В сечении 1-1 действует сила давления, направленная внутрь выделенного объема жидкости , в сечении 2-2 – сила ( – давление в сечениях 1-1 и 2-2, – площади сечений). На элементарной площадке стенки канала действуют: сила реакции стенки, равная силе давления pds и сила вязкого трения τds. Проекция этих сил на ось движения равна pds sin α + τds cos α (α – угол наклона элементарной стенки какала к его оси). Суммарная проекция внешних сил, действующих на изолированную массу жидкости, равна

.

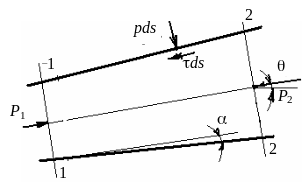
Рис. 2.37. Силы, действующие на поток жидкости в канале

Примем, что ось канала наклонена под углом θ к горизонту. Проекция веса жидкости, заключенной между выбранными сечениями равна gρVsin θ (V – объем выделенной массы жидкости).

Проекция всех сил, действующих на изолированную массу, равна

– gρVsin θ.

(2.40)

Распределение скорости в контрольных сечениях может быть неравномерным. Через элементарную площадку ds контрольной поверхности в единицу времени переносится количество движения, равное (u – местная скорость течения). Суммарное количество движения равно . Средняя скорость в контрольном сечении . Количество движения, подсчитанное по средней скорости равно

Отношение количества движения, действительно перенесенного потоком, к количеству движения, определенного по средней скорости, называется коэффициентом Буссинеска .

В единицу времени при установившемся движении изменение количества движения составит

,

где Q – расход жидкости.

Импульс действующих сил должен равняться изменению количества движения массы, на которую данный импульс действует. Следовательно, при течении жидкости в канале с учетом принятых условий соблюдается равенство

– gρVsin θ = .

(2.41)

Нами получено гидравлическое уравнение количества движения.

Вывод: При переходе от сечения 1-1 к сечению 2-2 проекция секундного количества движения потока изменяется на величину, равную сумме проекций всех внешних сил, действующих на объем потока, заключенный между сечениями 1-1 и 2-2.

Применяя уравнение количества движения, можно решить ряд задач гидравлики, например: теоретически определить коэффициент местного сопротивления при внезапном расширении трубы; изменение давления в трубе при равномерном отборе жидкости на одном ее участке; определение расхода газа при всасывании его через цилиндрическую трубу.