- •Курс лекций
- •Оглавление
- •Требования к обязательному минимуму содержания основной образовательной программы по направлению подготовки дипломированного специалиста «Строительство»
- •Лекция 1. Введение в предмет «Гидравлика». Основные свойства жидкостей и газов
- •1.1. Предмет гидравлики
- •1.2. История предмета
- •1.3. Капельные и некапельные жидкости
- •1.4. Силы, действующие в жидкости
- •1.5. Давление и его свойства
- •1.6. Основные физические свойства жидкостей
- •1.7. Вязкость. Идеальная жидкость
- •Практическое применение теоретических знаний Пример 1-1
- •Пример 1-2
- •Лекция 2. Основы гидростатики, динамики и кинематики жидкости
- •2.1. Тема 1. Равновесие жидкости
- •2.1.1. Дифференциальное уравнение равновесия жидкости. Поверхность равного давления
- •2.1.2. Основное уравнение гидростатики
- •2.1.3. Закон Паскаля
- •2.1.4. Абсолютное, манометрическое и вакуумметрическое давление
- •2.1.5. Сила давления на плоские и криволинейные поверхности
- •1. Сила давления на отдельный элемент поверхности.
- •2. Результирующая сила давления на стенку.
- •3. Сила давления жидкости на дно резервуара.
- •4. Сила давления на вертикальную прямоугольную стенку.
- •5. Сила давления на криволинейную поверхность.
- •6. Сила давления на цилиндрическую поверхность.
- •2.1.6. Относительный покой жидкости
- •2.1.7. Закон Архимеда
- •1. Равновесие твердого тела в жидкости.
- •2. Равновесие жидкости.
- •3. Условия равновесия плавающих тел.
- •2.1.8. Основное уравнение гидростатики для сжимаемой жидкости
- •2.1.9. Изотермическая атмосфера
- •2.1.10. Неизотермическая атмосфера
- •2.2. Тема 2. Основы кинематики и динамики жидкости и газа
- •2.2.1. Основные понятия кинематики жидкости
- •2.2.2. Уравнение неразрывности
- •2.2.3. Виды движения жидкости
- •2.2.4. Интегральная формула количества движения
- •2.2.5. Дифференциальное уравнение движения невязкой жидкости (уравнение Эйлера)
- •2.2.6. Общее уравнение энергии в интегральной форме (Уравнение Бернулли для потока реальной жидкости)
- •2.2.7. Три формы представления уравнения Бернулли для потока реальной жидкости
- •2.2.9. Особенности турбулентного и ламинарного течения жидкости. Число Рейнольдса
- •2.2.10. Уравнение Бернулли для элементарной струйки невязкой сжимаемой жидкости
- •2.2.11. Уравнение Бернулли для потока вязкой сжимаемой жидкости
- •Пример применения уравнения Бернулли для расчета коротких трубопроводов
- •Лекция 3. Основы моделирования гидромеханических процессов
- •3.1. Основы моделирования
- •3.2. Виды подобия. Масштабы моделирования
- •3.3. Критерии подобия
- •3.4. Конечно-разностная форма уравнения Навье-Стокса
- •3.5. Общая схема применения численных методов и их реализация на эвм
- •3.6. Измерительные приборы, используемые при проведении экспериментальных работ
- •1. Жидкостные манометры прямого действия.
- •2. Механические манометры.
- •3. Барометры.
- •4. Вакуумметры.
- •5. Трубка Пито–Прандтля.
- •6. Расходомер Вентури.
- •7. Ротаметры.
- •Лекция 4. Гидравлические сопротивления
- •4.1. Виды гидравлических сопротивлений
- •4.2 Сопротивление по длине при движении в цилиндрической трубе при ламинарном течении
- •4.3. Формула Дарси-Вейсбаха
- •4.4. Турбулентное движение в гидравлически гладких и шероховатых трубах
- •4.5. Движение жидкости в трубах некруглого сечения
- •4.6. Местные гидравлические сопротивления
- •4.7. Зависимость коэффициентов местных сопротивлений от числа Рейнольдса. Эквивалентная длина
- •4.8. Кавитация
- •4.9. Истечение жидкостей из отверстия в тонкой стенке
- •4.10. Зависимость коэффициентов истечения от числа Рейнольдса
- •4.11. Истечение из насадков
- •4.12. Виды насадков
- •4.13. Истечение при переменном напоре и под уровень жидкости
- •Пример применения уравнения Бернулли для расчета расхода через диафрагму
- •Лекция 5. Практическое применение законов гидравлики
- •5.1. Расчет короткого трубопровода
- •5.2. Расчет длинных трубопроводов
- •5.2.1. Понятие о простом и сложном напорных трубопроводах
- •5.2.2. Расчет трубопроводов, соединенных последовательно и параллельно
- •5.2.3. Гидравлический удар
- •5.2.4. Гидравлический таран
- •Пример расчета короткого трубопровода
- •Пример расчета магистрального трубопровода
- •Рекомендуемая литература
- •Дополнительная литература
- •Материально техническое обеспечение дисциплины
- •Требования к уровню знаний студентов
2.1.10. Неизотермическая атмосфера
Обычно температура воздуха с увеличением высоты уменьшается. Температура дымовых газов также быстро уменьшается в трубе. Для того, чтобы проинтегрировать основное уравнение гидростатики в этом случае необходимо знать закон изменения температуры с изменением высоты. Чаще всего для атмосферного воздуха принимают, что температура уменьшается по линейному закону
|
|
(2.26) |
где Т0 – температура на поверхности земли; a – градиент температуры.
Можно записать дифференциальное уравнение равновесия в следующем виде
|
|
(2.27) |
|
тогда
|
(2.28) |
Пример: Предположим, что температура понижается на 6ºС с увеличением высоты на 1000 м. Необходимо определить давление на вершине горы Монблан (z = 4800м), если на уровне моря температура Т0 = 30ºС.
Решение:
На вершине горы температура Т = 30 – 4800·0,006. Т = 274,2 К, тогда
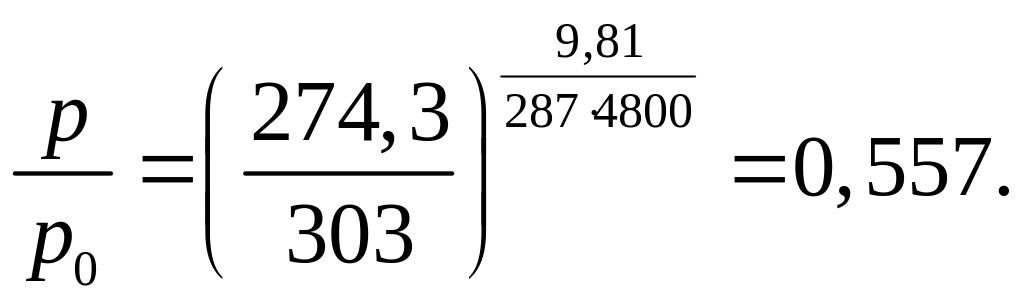
Вывод: Давление на вершине горы Монблан меньше почти в два раза.
Примеры решения практических задач гидростатики
Пример 2.1-1
К закрытому резервуару для определения
давления на свободной поверхности р0
присоединена стеклянная трубка.
Спрашивается, какое давление в резервуаре
р0, если вода в трубке поднялась
на высоту Н = 3 м? Трубка присоединена
на глубине
![]() =
2 м.
=
2 м.
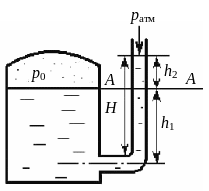
Рис. 2.24. К примеру 2.1-1
Ответ: Давление на поверхности воды в резервуаре = 107910 Па.
Пример 2.1-2
Определить разность давления в резервуарах А и В, заполненных водой, если разность уровней ртути в U-образном манометре h = 15 см.
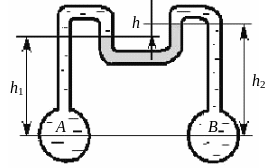
Рис. 2.25. К примеру 2.1-2
Ответ: Разность давлений в резервуарах – 18394 Па.
Пример 2.1-3
Определить суммарное усилие, воспринимаемое болтами смотрового люка диаметром d = 0,5 м, расположенного на глубине h = 3 м от свободной поверхности, на которой давление = 0,5 атм.
Ответ: Усилие, воспринимаемое болтами смотрового люка Р = 15700 Н.
Пример 2.1-4
При бурении скважины необходимо определить вес труб, опущенных в скважину, заполненную глинистым раствором плотностью ρр = 2800 кг/м3, длина труб l = 70 м. Один метр таких труб с муфтами в воздухе весит 300Н. Плотность стали ρст = 7500 кг/м3.
Ответ: Полный вес труб будет равен 902776 Н.
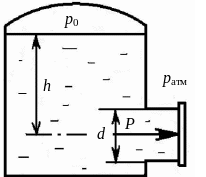
Рис. 2.26. К примеру 2.1-3
2.2. Тема 2. Основы кинематики и динамики жидкости и газа
Основные понятия: расход; мгновенная и средняя скорость; линия тока; трубка тока; уравнение неразрывности; установившееся и не установившееся движение жидкости; равномерное и неравномерное движение; сплошная среда; количество движения; момент количества движения; дифференциальное уравнение движения невязкой жидкости, общее уравнение энергии в интегральной форме; три формы представления уравнения Бернулли для потока реальной жидкости; турбулентный и ламинарный режимы течения жидкости; число Рейнольдса; осредненная и мгновенная скорости; пульсации; турбулентные касательные напряжения.
Вопросы, на которые необходимо найти ответ в ходе изучения темы:
Что называют линией тока, трубкой тока, элементарной струйкой?
Чем траектория движения частицы отличается от линии тока?
Какие свойства трубки тока вы знаете?
Зачем в гидравлике вводятся понятия: трубка тока, элементарная струйка, линия тока?
В чем суть математической модели Эйлера, которая применяется для описания движения жидкости?
Что такое расход жидкости, скорость, средняя скорость, живое сечение потока? Назовите единицы измерения.
Какова связь между массовым расходом и объемным?
Чем отличается установившееся движение жидкости от неустановившегося, равномерное от неравномерного? Приведите примеры.
Как записать вид движения жидкости в математической форме?
Привести примеры напорного и безнапорного движения жидкости.
Что называют сплошной средой?
Объяснить суть уравнения неразрывности.
Как уравнение неразрывности можно записать в математической форме?
Какие выводы можно сделать из уравнения неразрывности?
Для каких условий применима струйная расчетная модель движения реальной жидкости?
Как математически записать суммарную проекцию внешних сил, действующих на изолированную массу жидкости в наклонном канале?
Что называют коэффициентом Буссинеска?
Как записать изменение количества движения жидкости в единицу времени при установившемся движении жидкости?
Чему должен быть равен импульс действующих сил при движении жидкости?
Какие силы действуют на выделенный объем идеальной жидкости, движущийся равномерно?
Как записать уравнение равновесия движущегося равномерно объема идеальной жидкости?
Написать систему уравнений Эйлера и объяснить ее смысл.
Как из системы уравнений Эйлера получить уравнение Бернулли для струйки невязкой жидкости?
Как из уравнения Бернулли для струйки невязкой жидкости получить уравнение Бернулли для двух сечений потока реальной жидкости?
В чем отличие уравнения Бернулли для элементарной струйки идеальной жидкости от уравнения Бернулли потока реальной жидкости?
Для чего в уравнение Бернулли вводится коэффициент Кориолиса?
Какие выводы можно сделать из уравнения Бернулли?
Какие ограничения существуют в применении уравнения Бернулли?
Как построить линию полного напора, пьезометрическую линию?
В каком случае линия полного напора будет параллельна пьезометрической линии?
Записать уравнение Бернулли в форме удельной энергии и объяснить его суть.
Записать уравнение Бернулли в форме напоров и объяснить его суть.
Записать уравнение Бернулли в форме давления и объяснить его суть.
Для каких инженерных расчетов применяется та или иная форма записи уравнения Бернулли? Привести примеры.
Чем турбулентное движение жидкости отличается от ламинарного?
В чем физический смысл числа Рейнольдса, его практическое значение?
Чем характеризуется переходная зона от одного режима к другому?
Чему равно значение коэффициента Кориолиса при турбулентном и ламинарном режимах?
При каком режиме движения жидкости потери напора больше? Почему?
От каких параметров зависят гидравлические потери в ламинарном потоке?
Что такое пульсации скорости и давления, чем они вызваны, когда возникают?
В чем заключается теория Прандтля?
Что называют мгновенной, осредненной скоростью?
Чем осредненная скорость отличается от средней?
Практические задачи, решение которых может быть найдено после изучения теоретического материала:
Задача 2.2-1, 6
В закрытом резервуаре поддерживается постоянное манометрическое давление pм = 2 атм, под действием которого по трубе диаметром d1 = dн мм и общей длине l = 25 м (расстояние от начала до колена l1 = 5 м) вытекает жидкость при температуре t. Определить расход при напоре H1 = 2 м.

Рис 2.27. К задаче 2.2-1, 6
Примечание. Потерями напора пренебречь.
Задача 2.2-2, 7
Истечение происходит из открытого резервуара при постоянном напоре H1 = 5 м по короткому трубопроводу переменного поперечного сечения с диаметрами d1 = 10dн мм и d2 = 3dн мм в атмосферу. На втором участке трубопровода имеются два колена с плавным поворотом. Длина первого участка l1 = 0,8 м, длина второго участка l2 = 2 м. Определить скорость истечения u2 и расход Q2 через трубопровод.

Рис 2.28. К задаче 2.2-2, 7
Примечание. Потерями напора пренебречь.
Задача 2.2-3, 8
Из резервуара А, заполненного жидкостью на высоту H1 = 5 м и находящегося под манометрическим давлением рм = 20 кПа, жидкость подается по трубопроводу длиной l = 6 м и диаметром d = 10dн мм в резервуар В на высоту Н = 2 м. Определить расход Q и скорость протекающей по трубопроводу жидкости.
Примечание. Потерями напора пренебречь.
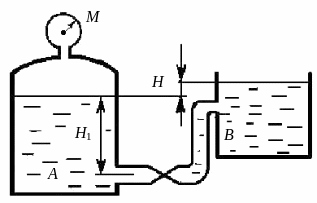
Рис. 2.29. К задаче 2.2-3, 8
Задача 2.2-4, 9
К закрытому резервуару, на свободной поверхности которого действует манометрическое давление рм = 10 кПа, подсоединен трубопровод переменного сечения с диаметрами d1 = 2dн мм и d2 = 5dн мм, заканчивающийся соплом диаметром dc = d1. Трубопровод подсоединен на глубине Н1 = м. На первом участке длиной l1 = 10 м установлен вентиль. Длина второго участка l2 = 5 м. Определить скорость истечения и расход Q вытекающей из сопла жидкости при температуре t и постоянном напоре H1.
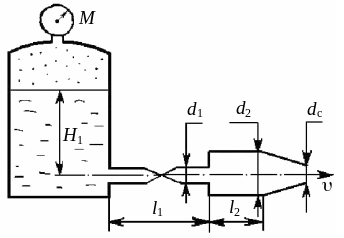
Рис. 2.30. К задаче 2.2-4, 9
Примечание. Потерями напора пренебречь.
Задача 2.2-5, 10
Центробежный насос подает воду с температурой t = 15 °С по трубе диаметром d = dн мм и длиной l = 27 м. Насос создает давление на выходе рн = 2,65 атм и подачу Q = л/с. Определить напор H, создаваемый насосом.
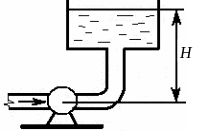
Рис. 2.31. К задаче 2.2-5, 10
Примечание. Потерями напора пренебречь.

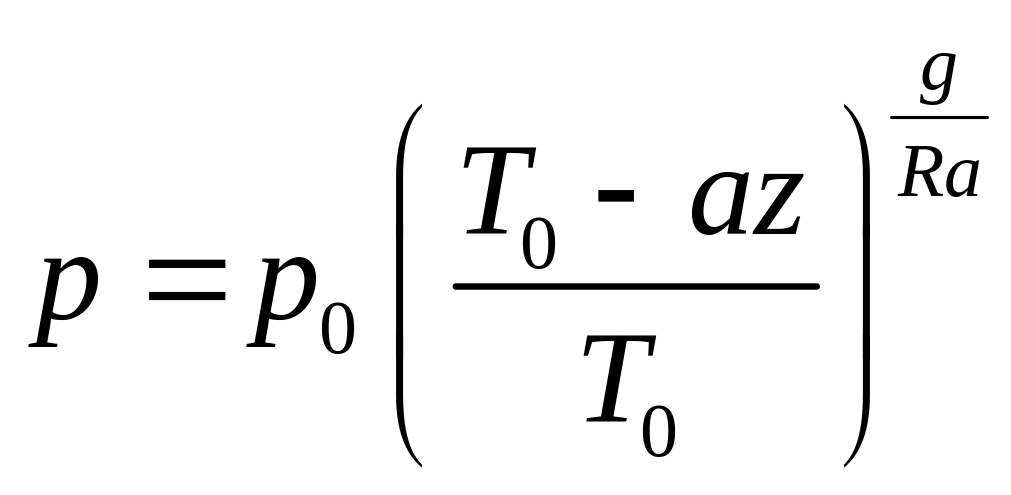 ,
или
,
или