Міністерство освіти і науки України
Національний університет “Львівська політехніка”
Реєстр. № 2102
від 19.04.2007
Прискорений пошук усталених режимів електромаґнетних елементів систем керування
Інструкція до лабораторної роботи № 3
з курсу “Моделювання процесів
та елементів систем керування”
для студентів базового напрямку 6.0914
“Комп’ютеризовані системи, автоматика і управління”
Затверджено
на засiданнi кафедри
“Комп’ютеризовані
системи автоматики»
Протокол №10 від30.03.2007 р.
Львів 2007
Прискорений пошук усталених режимів електромаґнетних елементів систем керування: Інструкція до лабораторної роботи №3 з курсу “Моделювання процесів та елементів систем керування” для студентів базового напрямку 6.0914 “Комп’ютеризовані системи, автоматика і управління” / Укл.: У.Ю.Дзелендзяк, А.Г.Павельчак, В.В.Самотий – Львів: ДУЛП, 2007. – 16 с.
Укладачі: У.Ю.Дзелендзяк, к.т.н., ст.викл.
А.Г.Павельчак, асистент
В.В.Самотий, д.т.н., професор
Відповідальний за випуск
А.Й.Наконечний, д.т.н., професор
Рецензент: З.Р.Мичуда, д.т.н., професор
Мета роботи – вивчити методи прискореного пошуку усталених режимів електромаґнетних елементів систем керування, а також дослідити ці режими для заданої схеми використовуючи числові методи розв’язування систем нелінійних диференціальних рівнянь.
Основні теоретичні відомості
Таким чином, маючи систему диференціальних рівнянь, що описує стан пристрою і початкові умови, з допомогою чисельних методів ми можемо розрахувати перехідні процеси що в них протікають. Наступною задачею, яка викликає великий інтерес є аналіз усталених режимів роботи електромаґнетних елементів систем керування. Рівняння динаміки дають можливість проводити аналіз перехідних процесів. Інтеґруючи ці рівняння на достатньо великому інтервалі часу, отримаємо усталений режим. Безумовно, що такий підхід має два недоліки: 1) накопичення похибок чисельного інтеґрування; 2) значні затрати машинного часу. Тому розглянемо ряд методів, які позбавлені цих недоліків, дають можливість отримувати розв’язок в часовій області і з наперед заданою точністю збіжності ітераційного процесу. Як і усі ітераційні методи вони дуже зручні при програмуванні.
1.1. Модель чутливостей до початкових умов
Один з методів, що дає можливість проводити аналіз усталених режимів базується на ітераційних циклах Ньютона, або як його ще називають – модель чутливостей до початкових умов. Він дає можливість знаходити такі початкові умови, які при інтеґруванні рівнянь динаміки приводять до усталеного режиму.
В
усталеному режимі змінні стану
повинні задовольняти умову періодичності,
яку запишемо у вигляді певного нелінійного
рівняння
(1)
де
– період вхідної дії.
Нелінійне рівняння (1) розв'язуємо ітераційним методом Ньютона
(2)
де
– якобіан рівняння періодичності.
Диференціюючи (2) за
отримаємо
(3)
де
– матриця монодромії. Запишемо її у
вигляді добутку двох інших матриць. Для
цього часткову похідну (3) запишемо як
похідну складної функції
(4)
де
– матриця коефіцієнтів рівнянь динаміки;
– матриця додаткових чутливостей.
Останню визначаємо в результаті
інтеґрування додаткової системи
диференціальних рівнянь першої варіації.
Для цього продиференціюємо за часом
матрицю S
.
(5)
Запишемо диференціальні рівняння прикладу розглянутого в лабораторній роботі № 2
,
(6)
де
– вектор змінних стану;
– матриця коефіцієнтів
.
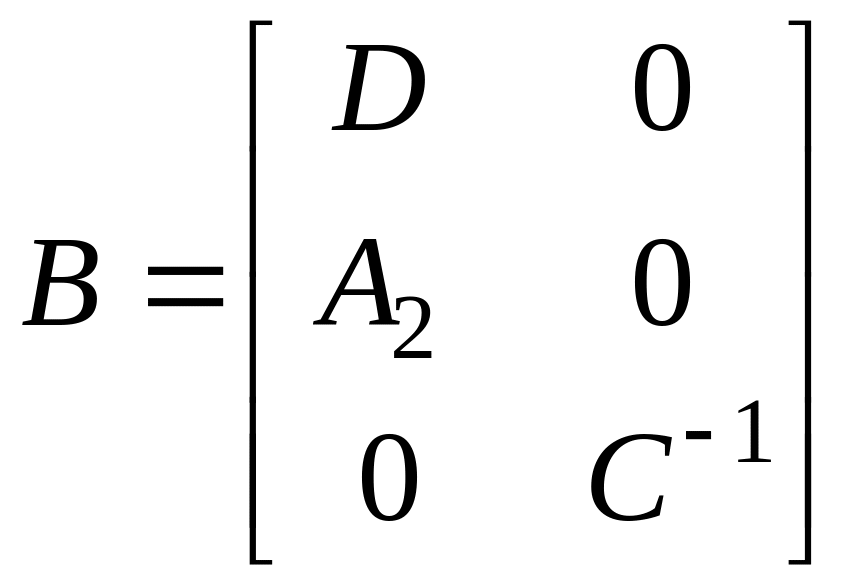(7)
Тут
– матриці
коефіцієнтів, причому
Запишемо рівняння (5) як похідну складної функції
.
(8)
Обчислимо часткову похідну для матриці коефіцієнтів
(9)
Враховуючи,
що
,
,
матрицю
(9) запишемо у вигляді
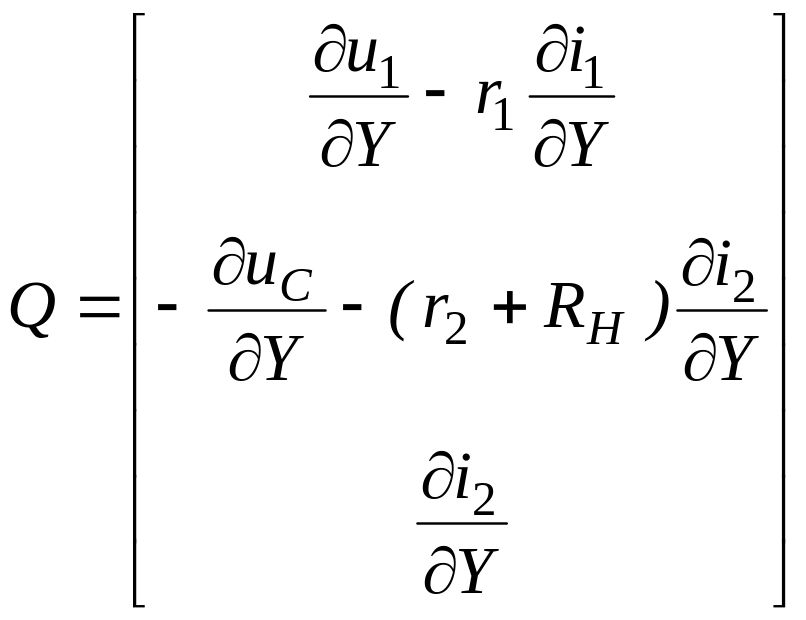(10)
Маючи рівняння динаміки можна обчислити часткові похідні матриці , а саме
,
(11)
де
,
.
Підставивши (11) в (10) отримаємо остаточний вираз для матриці
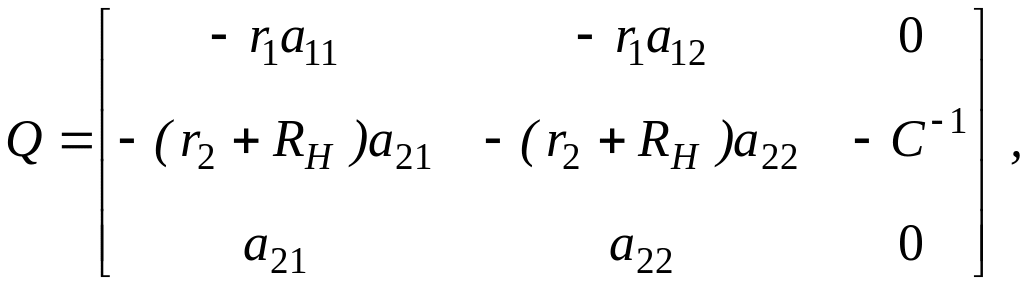(12)
Рівняння (5) запишемо у матричній формі
(13)
Рівняння
(13) завжди лінійне. Його інтеґруємо
сумісно з нелінійним рівнянням (6).
Початкове наближення
задаємо довільним, як правило, нульовим.
Початкові умови
згідно (2.6), (2.7) повинні строго задовольняти
умову
(14)
Ітераційний процес (2) зупиняємо при виконанні нерівності
(15)
де
– помилка збіжності ітераційного
процесу.