
- •62. Инвариантность и чувствительность систем управления
- •63. Математические модели объектов и систем управления
- •1) При последовательном соединении звеньев их передаточные функции перемножаются.
- •2) При параллельном соединении звеньев их передаточные функции складываются.
- •3) Замкнутая система (система с обратной связью).
- •Фазовая частотная характеристика звена на частоте входного сигнала показывает, на сколько выходной сигнал сдвинут по фазе (углу) относительно входного сигнала.
- •64. Формы представления моделей
- •65. Методы анализа и синтеза систем управления
- •66. Цифровые системы управления
- •1. Нестабильность параметров.
- •2. Сложность централизованного управления несколькими объектами.
- •3. Сложность серийного производства аналоговых систем управления.
- •67. Использование микропроцессоров и микро-эвм в системах управления
- •68. Особенности математического описания цифровых систем управления, анализа и синтеза систем управления с эвм в качестве управляющего устройства
- •69. Программная реализация алгоритмов управления в цифровых системах
- •70. Основные понятия теории моделирования
- •71.Классификация видов моделирования имитационные модели информационных процессов
- •72. Имитационные модели информационных процессов
- •73. Математические методы моделирования информационных процессов и систем
Фазовая частотная характеристика звена на частоте входного сигнала показывает, на сколько выходной сигнал сдвинут по фазе (углу) относительно входного сигнала.
Годографом
частотной характеристики
называют траекторию, которую описывает
конец радиус-вектора, длина которого
равна АЧХ системы, а угол поворота –
ФЧХ (рисунок 2.9). Координатами годографа
в комплексной плоскости являются функции
![]() при изменении аргумента
при изменении аргумента
![]() в пределах
в пределах
![]() .
.
Переходной
функцией системы
![]() называют ее отклик на входное воздействие
в виде единичной ступенчатой функции,
при условии, что на момент поступления
воздействия система находилась в покое
(что соответствует нулевым начальным
условиям).
называют ее отклик на входное воздействие
в виде единичной ступенчатой функции,
при условии, что на момент поступления
воздействия система находилась в покое
(что соответствует нулевым начальным
условиям).
Импульсной
характеристикой системы
![]() называют ее отклик на входное воздействие
в виде дельта-функции при условии, что
на момент поступления воздействия
система находилась в покое.
называют ее отклик на входное воздействие
в виде дельта-функции при условии, что
на момент поступления воздействия
система находилась в покое.
64. Формы представления моделей
Математическое описание. Уравнения статики и динамики. Линеаризация.
Любой процесс или объект можно описать дифф или разностными уравнениями. Ур-е динамики описывает процессы в системе при произвольных вх воздействиях в течение времени. Ур-е статики описывает процессы в системе при постоянных вх воздействиях в установивш режиме. В основном системы описыв нелинейн дифф ур-ями, что затрудняет исследование системы и объекта. Замена нелинейного ур-я линейным нзв линеаризацией.
Передаточной функция звена или системы – отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.
Математическое описание. Частотные характеристики.(АФЧХ, ЛАХ и ЛФХ)
Если
на вход звена (системы) подать гармоническое
воздействие
![]() ,
то после окончания переходных процессов
на выходе устанавливаются колебания
,
то после окончания переходных процессов
на выходе устанавливаются колебания
![]() той
же частоты, но иной амплитуды и сдвинутые
по фазе относительно входных колебаний.
той
же частоты, но иной амплитуды и сдвинутые
по фазе относительно входных колебаний.
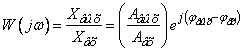 – амплитудно-фазовая
характеристика есть отношение выходной
величины к входной величине выраженной
в комплексной форме.
– амплитудно-фазовая
характеристика есть отношение выходной
величины к входной величине выраженной
в комплексной форме.
![]() – АЧХ
– АЧХ
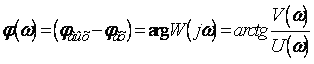 –
функция частоты –
ФЧХ
–
функция частоты –
ФЧХ
Математическое описание. Временные характеристики.
Временная характеристика звена системы – закон изменения выходной величины в функции времени при изменении входной величины по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое. Зависит от характера звена.
Переходная функция звена – реакция звена на единичное ступенчатое воздействие.
Y(p)=W(p)*X(p); H(p)=>W(p)/p; L{1(t)}=1/p; h(t)=L-1[W(p)/p]
Импульсная переходная или весовая функция – реакция звена на импульсное воздействие в виде δU
Y(p)=W(p)*X(p); L[δ(t)]=1; K(p)=W(p)*1; k(t)=L-1[W(p)]; W(p)=pH(p)=k(p); k(t)=dh/dt
Достоинством временных характеристик является то, что они могут быть получены экспериментально.
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.
Для математического моделирования линейных непрерывных САУ используются дифференциальные уравнения.
Формы представления моделей
Выше указывалось, что для анализа систем автоматического управления и регулирования широко используется моделирование. Формы представления моделей САУ могут быть самыми различными. Среди них наиболее распространенными являются:
представление САУ с помощью дифференциальных или разностных уравнений;
представление в виде структурных схем с использованием передаточных функций и последующего разбиения на отдельные типовые динамические звенья;
представление в виде цифровых фильтров для последующего моделирования с помощью ПЭВМ;
представление в форме аналоговых моделей для последующей реализации с использованием операционных усилителей.
