Глава 2.

Практическая часть.

Математическая модель – это система уравнений, которая устанавливает взаимосвязь между входными и выходными параметрами реактора. Математическая модель реактора должна содержать минимальное количество уравнений при сохранении качественных и количественных характеристик реактора. Математическую модель реактора рассматривают по четырём уровням:

Уравнение материального баланса.

Уравнение теплового баланса.

Кинетическое уравнение (или уравнения, если в реакторе протекает несколько реакций).

Уравнение, описывающее гидродинамическую обстановку в реакторе.

Для упрощения математической модели вводят допущения, которые существенно упрощают математический аппарат, при этом не изменяют сущность рассматриваемого объекта. Применительно к химическому реактору, наибольшую сложность представляют уравнения, описывающие гидродинамическую обстановку в реакторе. Поэтому были созданы модели идеализированных реакторов, в которых характер движения реагентов ограничивается двумя режимами: полного смешения и идеального вытеснения.

При рассмотрении модели полного смешения устанавливаются следующие допущения:

Значения параметра во всех точках реакционного объёма одинаково.

Значение параметра на выходе из реактора равно значению параметра в объёме реактора.

Изменение значения параметра начального до конечного значения происходит за нулевой промежуток времени. Диапазон изменения параметра определяется объёмом реактора.

Дегидрирование бутана проводят в адиабатическом реакторе полного смешения.

Кинетическое уравнение:

U=k₊*(PC₄H₁₀/PC₄H₈)*(1-PC₄H₈*PH₂/(PC₄H₁₀*Kp)) (м³С₄H₁₀/м³*с)

Зависимость константы скорости прямой реакции от температуры:

Lg(K₊)=9,6-9050/T

Зависимость константы равновесия от температуры:

lgKp=-6700/T +7.574

Определить наилучший температурный режим реактора полного смешения и производительность по бутену, если исходный состав (мольные доли): бутан 0.1-0.3, бутен 0,01, водород 0,02, остальное – азот, расход смеси 10000-20000 м³/ч, температура смеси на входе в реактор 800-1100 К, давление 0,5-2 Мпа

Программный код:

Нами были получены следующие графики и зависимости:

Так как адиабатический коэффициент нашей задачи имеет отрицательный знак то температура в адиабатическом реакторе будет ниже, а значит константа равновесия и константа скорости будут меньше при адиабатическом ,чем при изотермическом режиме реактора. Следовательно, при одинаковом объёме реактора степень превращения при изотермическом режиме будет выше. Таким образом, выгоднее будет использовать изотермический режим.

На данной графической зависимости видно, что производительность изотермического реактора выше, чем адиабатического реактора. Это обусловлено тем, что степень превращения при реализации изотермического режимавыше чем в адиабатическом реакторе. Следовательно, максимальная производительность н-бутилена обеспечивается при использовании изотермического температурного режима.

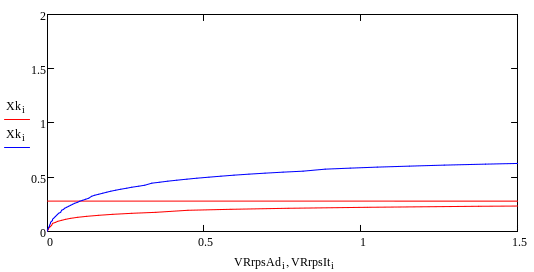
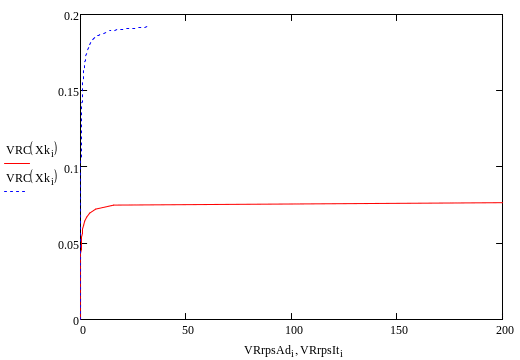
Рассмотрим изменения производительности в температурном интервале 800-1200:

Приведем и рассмотрим три графических зависимости для производительности, меняя входную температуру реактора.

Т=800К

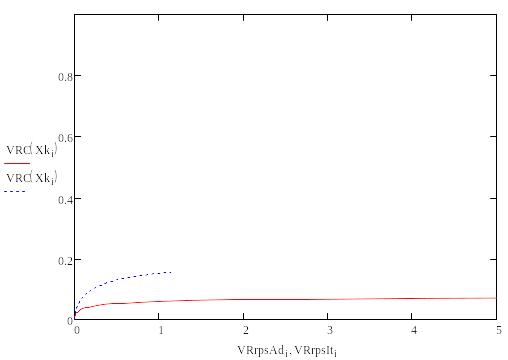
Т=1000К

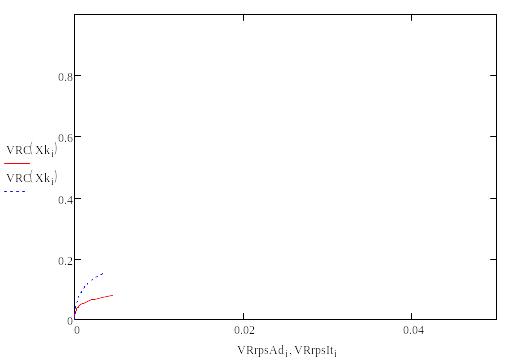
Т=1200К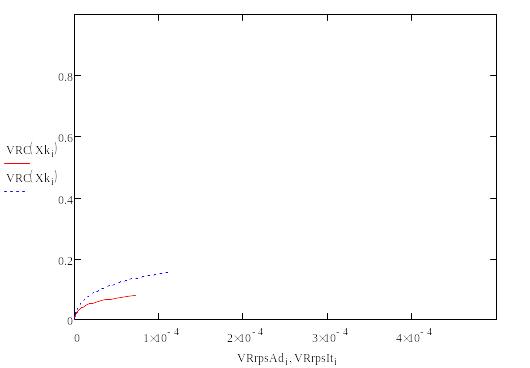

Как мы видим, увеличение исходной температуры приводит к незначительному увеличению производительности, точнее её максимального порога, но на достижении одинаковой производительно требуется гораздо меньший объем реактора.

Теперь рассмотрим как влияет на производительность увеличение давления в реакторе. Приведем соответствующие графические зависимости.

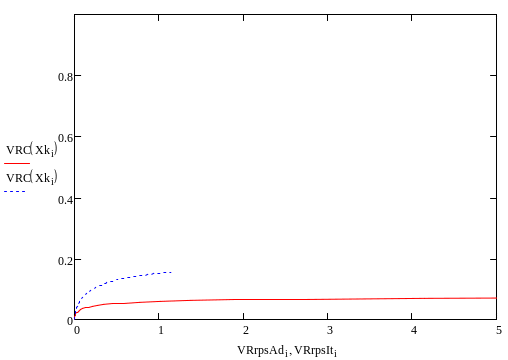
р=1 атм

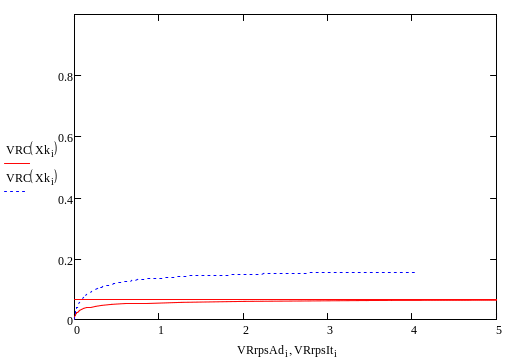
р=2 атм

Мы видим что наиболее оптимальные значения ниже атмосферного. Именно при этих значения для достижения заданного значения производительности потребуется наименьший по объему реактор.

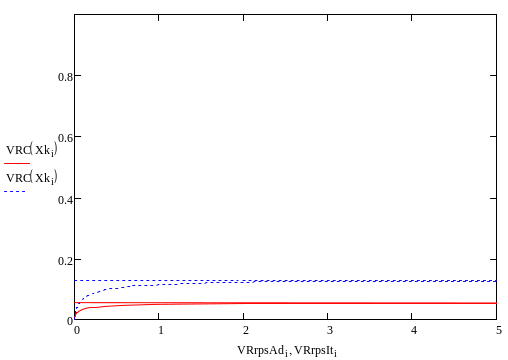
Рассмотри влияние на производительность увеличение объемного расхода реагентов:

VNS=10000

VNS=15000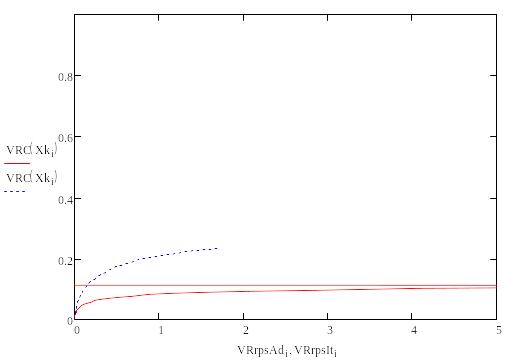

VNS=20000

Мы видим что увеличение объемного расхода приводит к увеличению максимального значения производительности, и мы видим что при одном и том же объеме реактора значение производительности с увеличением расхода реагентов увеличивается.

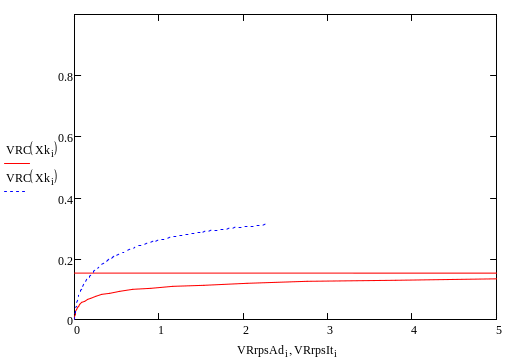
Рассмотрим, как будет влиять на производительность изменение начальной концентрации н-бутана.

ZNA=0.1

ZNA=0.2

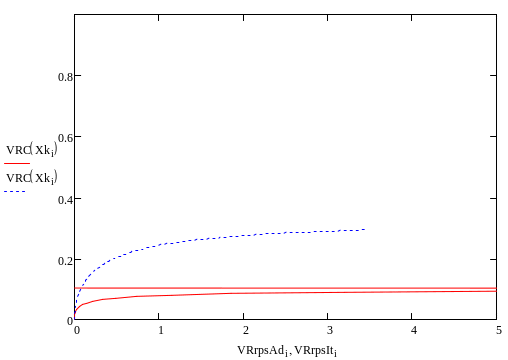
ZNA=0.3

Мы видим что увеличение начальной концентрации н-бутана приведет к увеличению как максимального значения производительности, так и приведет к уменьшению объема реактора необходимого для достижения одинакового значения производительности.

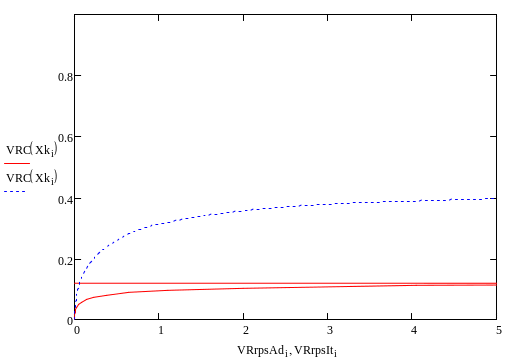
Вывод

Таким образом мы рассмотрели и смоделировали процесс дегидрирования н-бутана до н-бутилена. В первой части нашей работы мы описали общие сведения о процессе, способы реализации процесса реализуемые в промышленности, справочные данные по используемым нами веществам.

Во второй части мы создали и описали модель дегидрирования н-бутана, с помощью ЭВМ. На основе результатов моделирования мы смогли делать выводы, что максимальная производительность процесса будет достигаться в изотермическом режиме, при пониженном давлении, кроме того , производительность процесса увеличивает повышение объемного расхода реагентов, повышение начальной концентрации, и увеличение входной температуры.