Ортогональні підпростори
Нехай
(
– підпростори евклідового простору
).
Озн.
Підпростори
називаються ортогональними (позначається
),
якщо
.
Твердження.
коли кожний базисний вектор
ортогональний до кожного базисного
вектора
.
Доведення.
Нехай
– базис
;
– базис
.
1) (
)
Доведемо, що
.
За
означенням ортогональності для
2) (
)
Доведемо, що
Нехай
Якщо
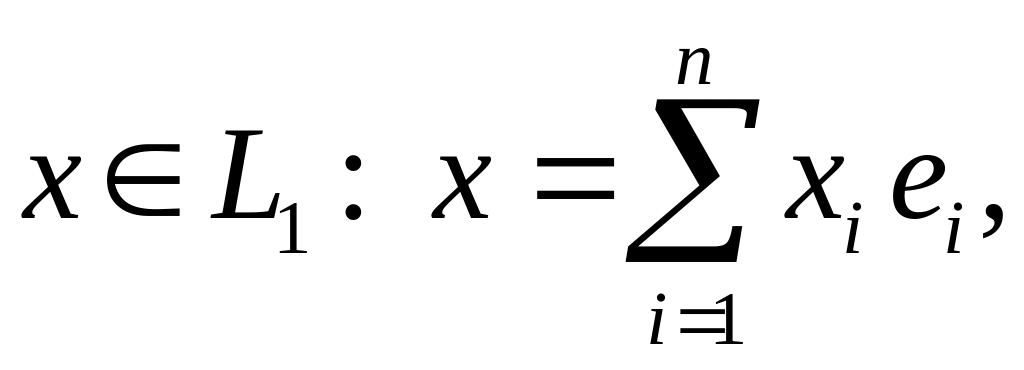а
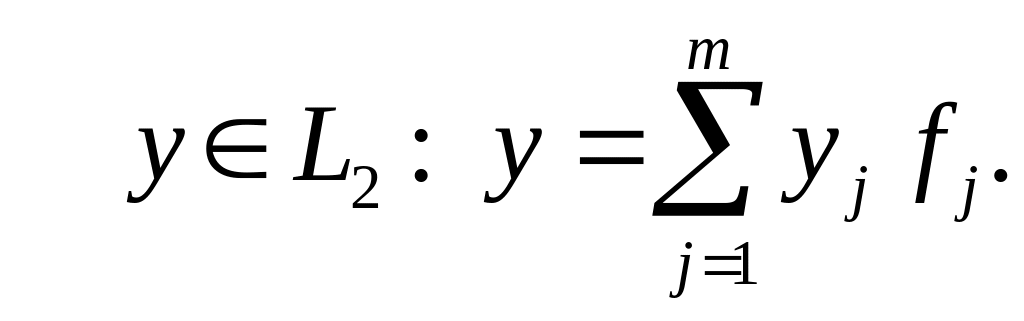
Тоді
Ортогональна сума підпросторів
Озн.
Сума
ортогональних підпросторів
і
називається ортогональною сумою і
позначається
.
Твердження.
Ортогональна сума ненульових підпросторів є прямою.
Доведення.
.
Нехай – ортонормований базис ;
– ортонормований
базис
.
Тобто
Розглянемо
систему
.
(*)
Зрозуміло,
що кожний вектор
виражається через вектори системи (*).
Але система (*) складається із попарно ортогональних векторів, тому вона є лінійно-незалежною.
Тобто
система (*) є повною в
і лінійно-незалежною
вона є базисом
є прямою, що і треба було довести. Тобто
.
Ортогональне доповнення.
Нехай
(
–
не обов’язково підпростір, може бути
якась непуста множина);
.
Озн.
Ортогональним доповненням простору
називається
Твердження.
– лінійний підпростір
.
Доведення.
Нехай
Тоді
тому що для
Скористалися
тим, що
.
Теорема.
Будь-який
евклідів простір
є ортогональною сумою будь-якого свого
лінійного підпростору
і його ортогонального доповнення, тобто
Доведення.
Нехай
– ортогональний базис
,
а
– ортогональний базис .
Система
– ортогональна
вона лінійно-незалежна.
Якщо вона не є базисом , то її можна доповнити до ортогонального базису .
Нехай вектор
–
якийсь доданий базисний
вектор.
Вектор
до всіх
,
з іншого боку
до всіх
Але
–
пряма сума, для такої суми
Таким чином, базисом є об’єднання базисів і , що і доводить теорему.
Наслідок.
Оператори в евклідових (унітарних) просторах Спряжений оператор.
Озн. Унітарний простір – це евклідів простір над полем комплексних чисел.
Нехай – лінійний оператор, який діє в унітарних просторах.
Озн.
Оператор
називається спряженим до
,
якщо
виконується
Оператор має наступні властивості:
1.
2.
3.
4.
5.
Доведемо властивості 1 та 3.
1)
Через
те, що ця рівність виконується для
.
2)
Доведення властивості 5 див. у підручнику Воєводіна «Лінійна алгебра» стор. 242.
Матриці спряжених операторів в ортобазисі.
Нехай
у просторі
зафіксовано ортонормований базис
,
а у просторі
– ортонормований базис
.
І нехай
у цих базисах побудовано матрицю
операторів
і
з елементами
та
.
Як відомо
Так само
і для
:
Тобто
чи
Якщо
,
то
Самоспряжений оператор
Нехай – лінійний оператор, який діє в унітарному просторі .
.
Озн.
Оператор
називається самоспряженим, якщо
,
чи, іншими словами:
Властивості самоспряженого оператора.
1. Власні числа самоспряженого оператора – дійсні.
Доведення.
Так, як
2. Власні вектори, які відповідають різним власним числам самоспряженого оператора, ортогональні.
Доведення.
.
.
Тобто
що і треба було довести (оскільки
).
3. Спектральна теорема для самоспряженого оператора (без доведення).
Для будь-якого самоспряженого оператора існує ортонормований базис з власних векторів. Матриця оператора в такому базисі набуває діагонального вигляду.
.
4. Якщо
у просторі
зафіксувати ортонормований базис
,
побудувати матрицю самоспряженого
оператора
,
то її коефіцієнти
Така матриця називається симетричною за Ермітом.
Частковий випадок.
У дійсному
просторі
– матриця
– симетрична.