Перехід до іншого базису Перетворення координат вектора при зміні базису

Нехай – лінійний простір; ; – базис цього простору, який ми умовно будемо називати «старим».

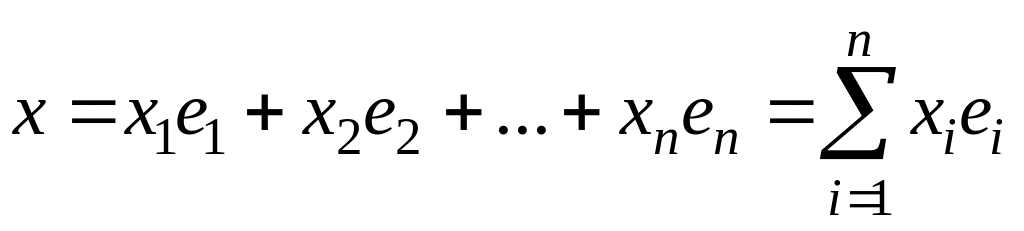Якщо , то: . (1)

Таким чином, кожному елементу можна поставити у взаємно однозначну відповідність стовпчик координат цього вектора за «старим» базисом:

.

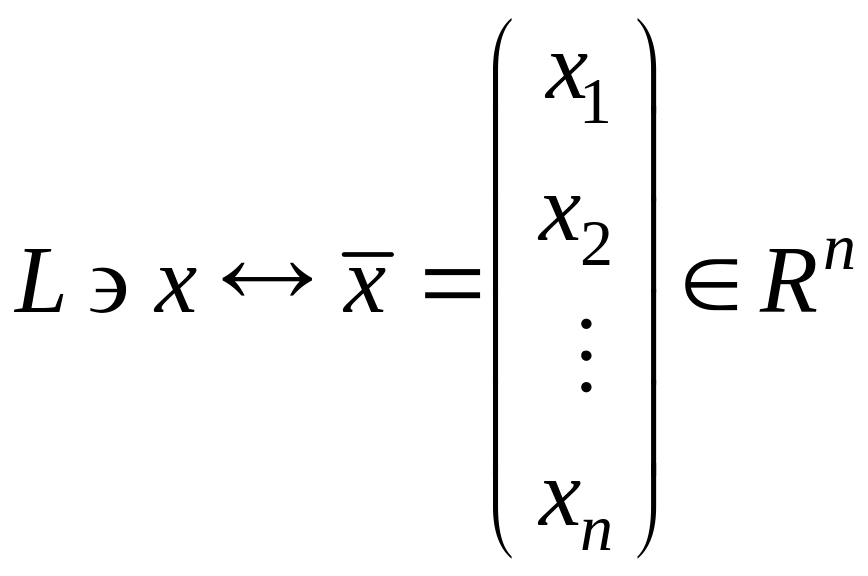Якщо ж взяти в тому ж просторі якийсь інший («новий») базис , то той же вектор можна розкласти за ним і отримати стовпчик «нових» координат: 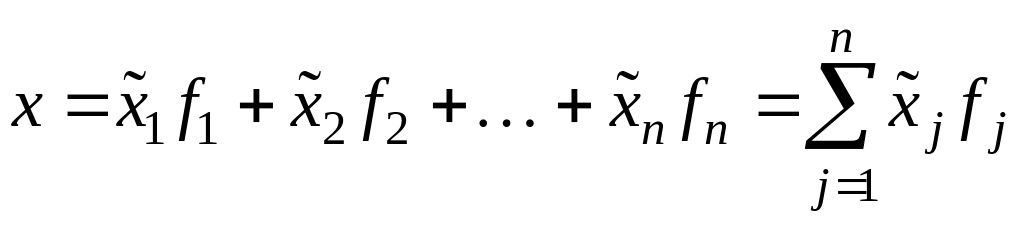. (2)

Тобто, тому ж самому елементу відповідатиме інший стовпчик:

.

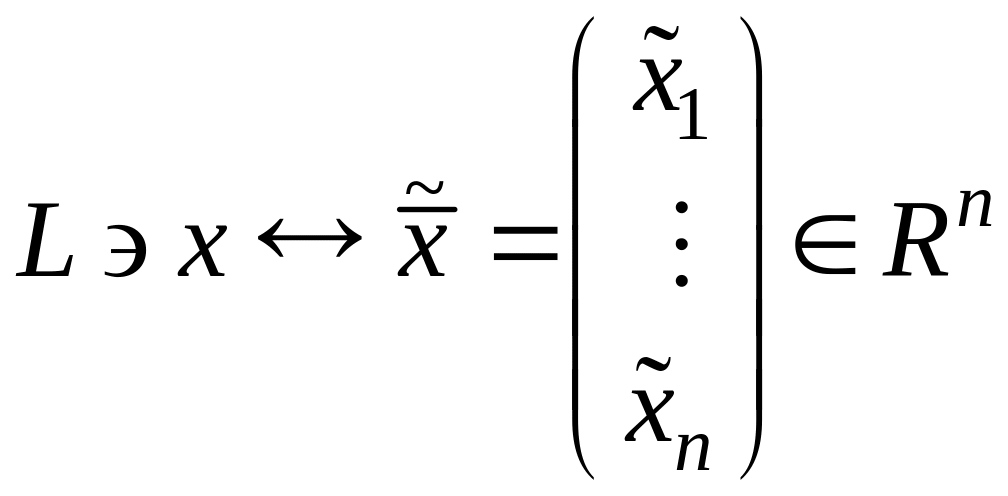Нам треба знайти зв’язок між стовпчиками та .

Побудуємо так звану матрицю переходу . Для цього:

а) кожний вектор «нового» базису по черзі розкладемо за «старим»:

;

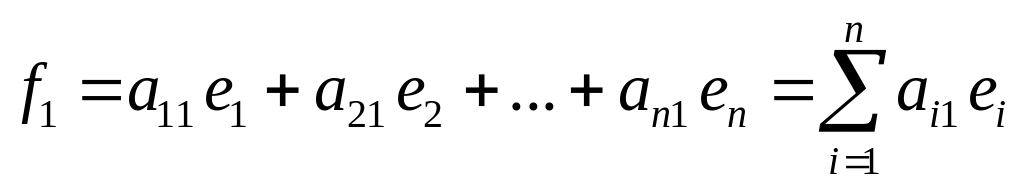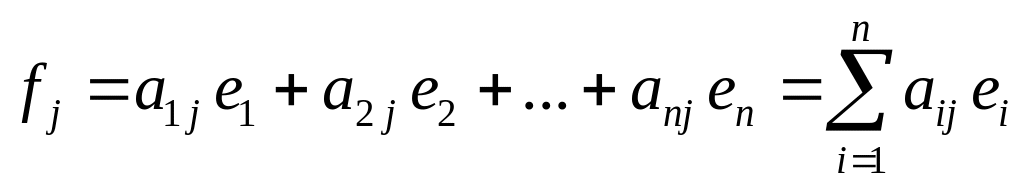, і т.д.; (3)

б) коефіцієнти розкладу запишемо стовпчиками.

.

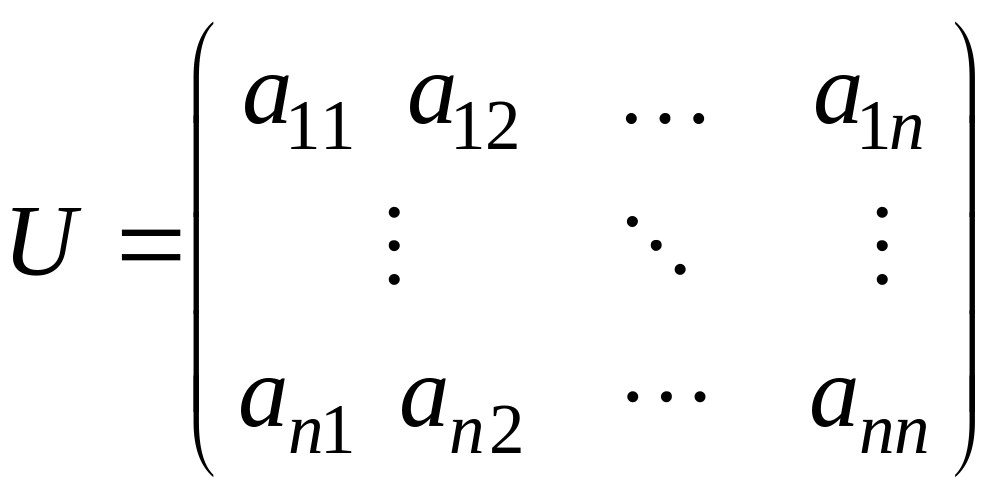З виразів (2) та (3) маємо,

.

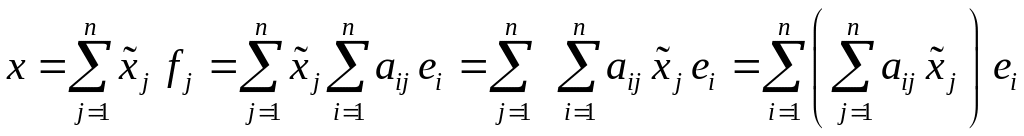Порівнюючи отриманий результат із виразом (1), маємо: .

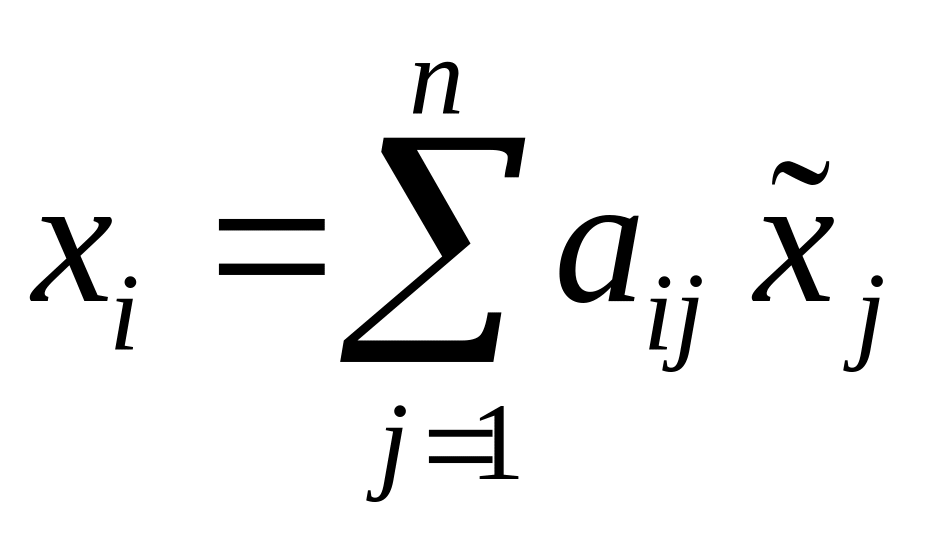Це є покоординатний запис співвідношення .

Тоді, .

Зауваження. оскільки її стовпчики – координати лінійно незалежних базисних векторів. А це означає, що завжди існує.

Приклад. Знайти координати розкладу вектора за базисом

Розв’язання. Координати векторів задані в канонічному базисі Нам зручно саме його вважати «старим», а - «новим». Тоді матриця переходу .

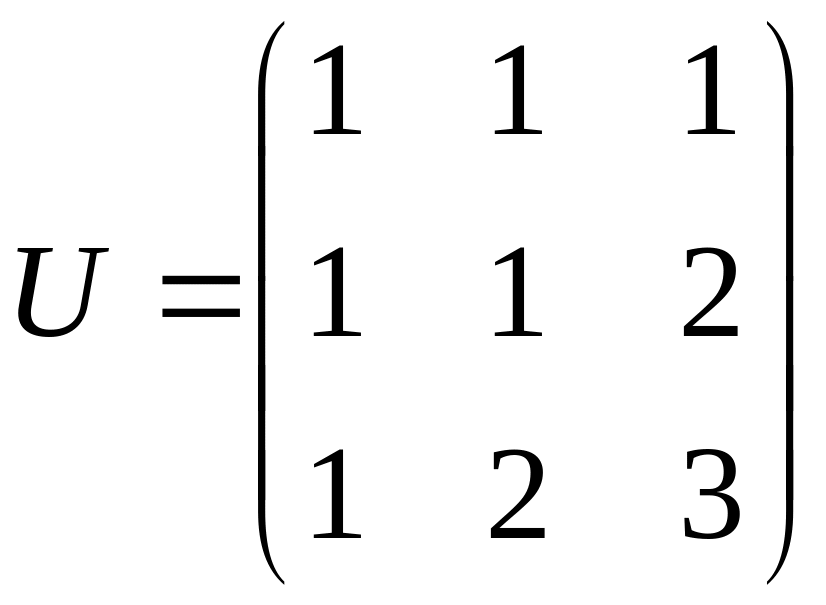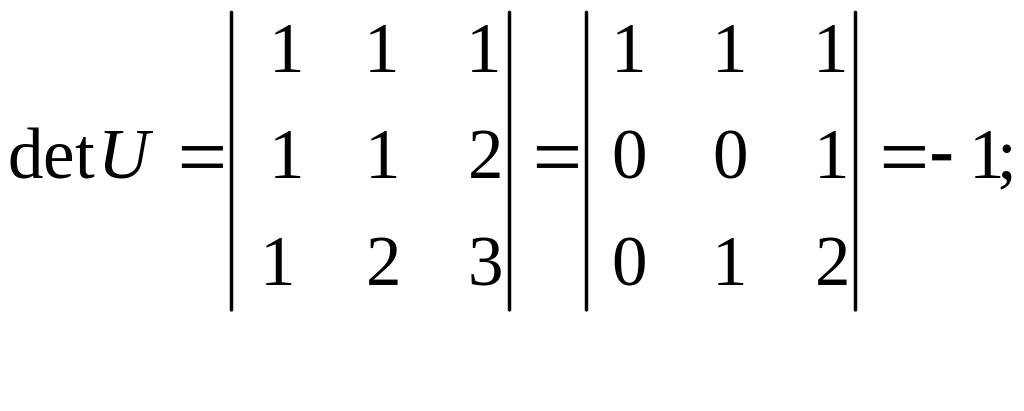
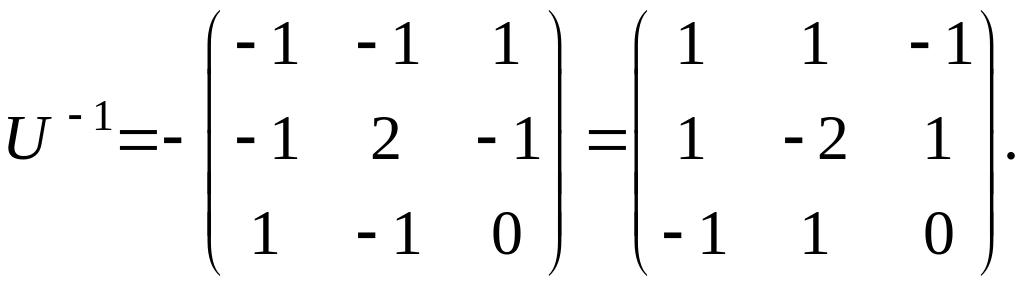
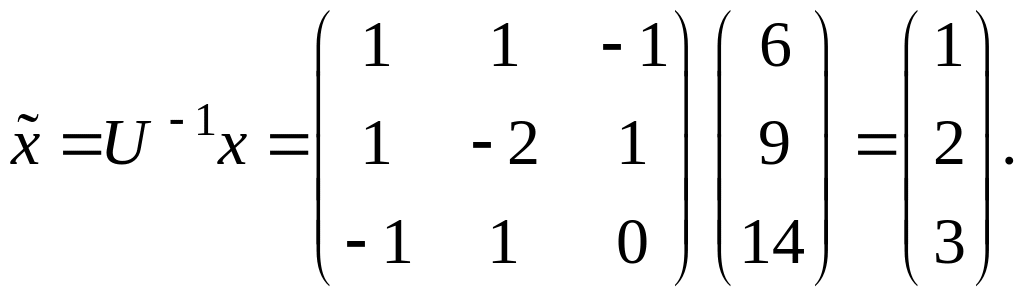
Можна переконатись, що дійсно

Матриця лінійного оператора при зміні базису

Нехай – деякий лінійний оператор, який діє із лінійного простору у простір . .

І нехай ; – «старий» базис ; ; – «старий» базис .

У цих базисах можемо побудувати матрицю оператора .

Якщо у просторі перейти до базису , а у просторі до базису , то у цих «нових» базисах матриця того ж оператора зміниться – . Треба знайти зв’язок між цими матрицями.

Побудуємо дві матриці переходу: – у просторі ; – у просторі . Тоді операторному співвідношенню ; ;

відповідають матричні:

; (1)

; (2)

Але, ; . Підставляємо у (1):

.

Порівнюючи із (2), маємо: ,

і навпаки. .

Для нас буде важливим такий окремий випадок: .

І у першому, і у другому «екземплярі» простору базис – «новий», а – «старий», матриця переходу – .

Тоді .

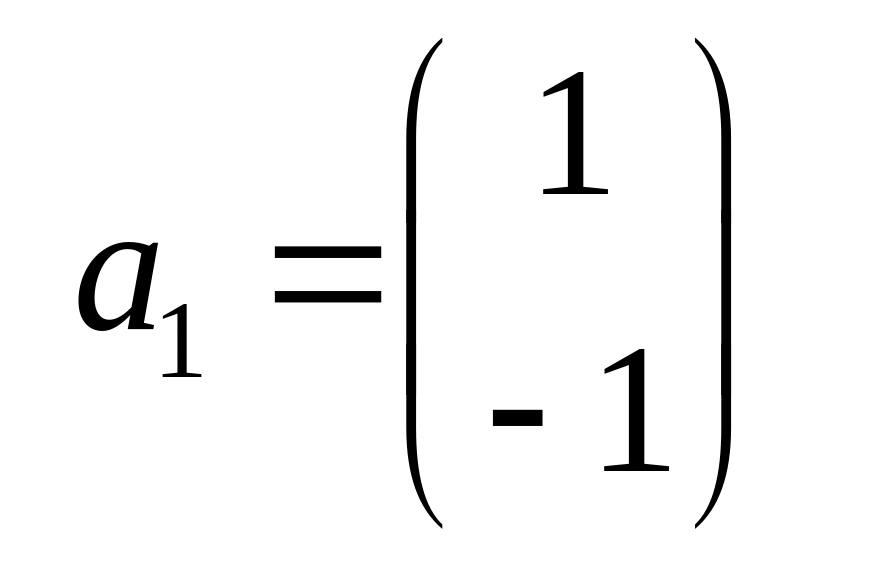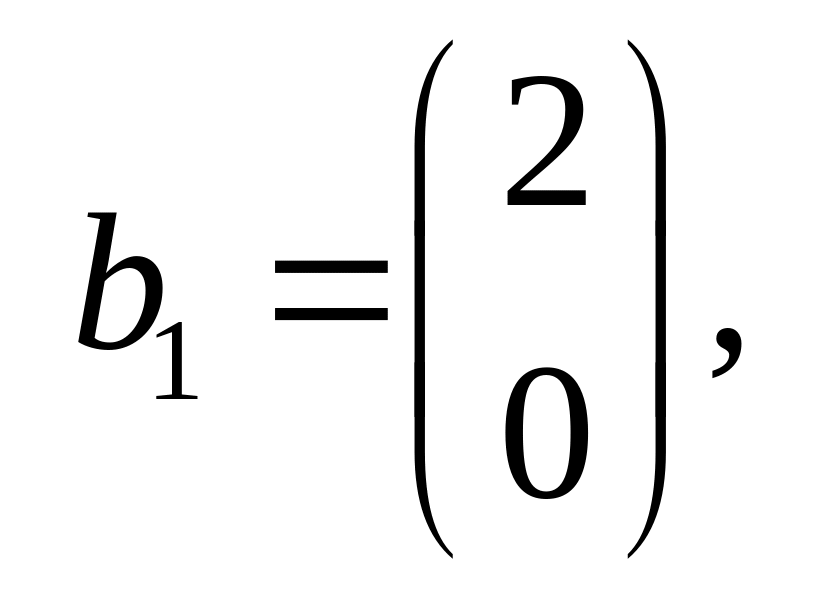
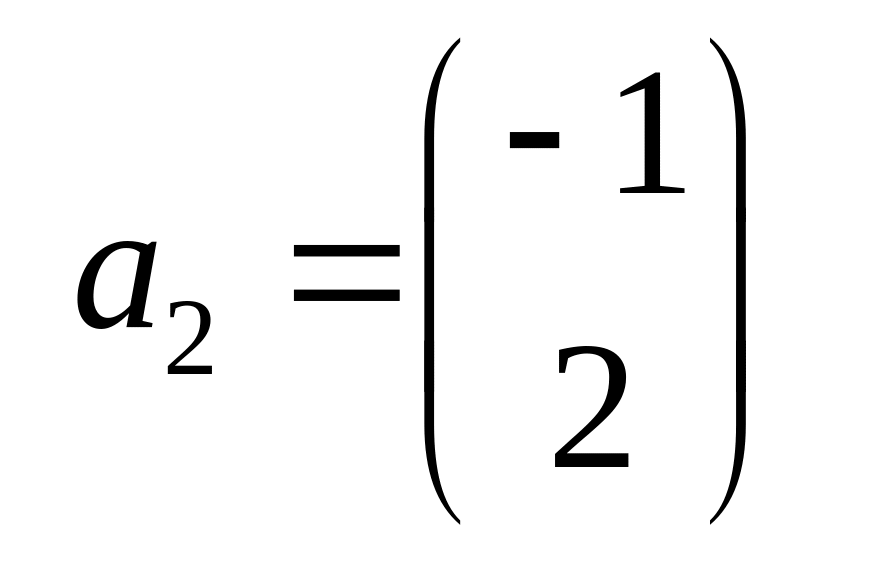Приклад. Оператор переводить вектори в в 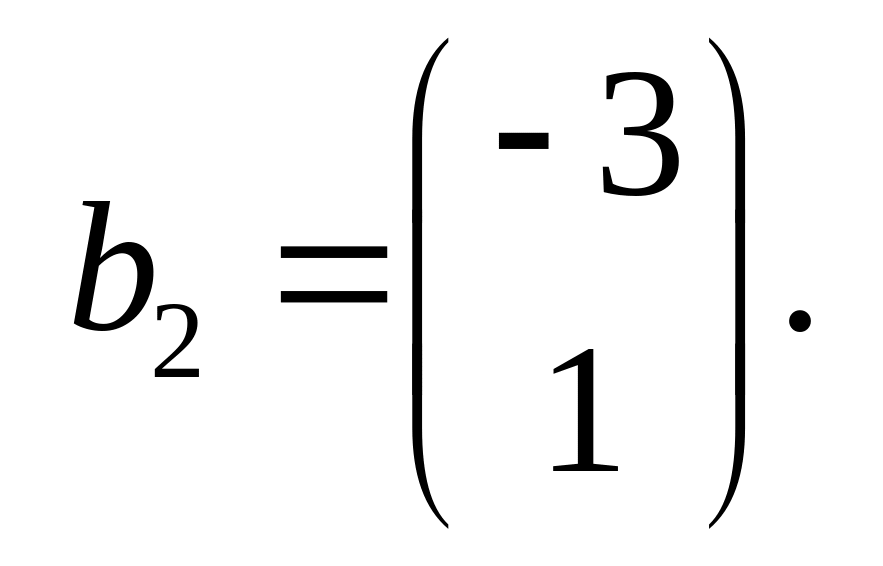Знайти матрицю оператора : а) в базисі ; б) в канонічному базисі.

Розв’язання.

а) Щоб побудувати матрицю оператора в базисі , треба і розкласти за тим же базисом, коефіцієнти розкладу записати стовпчиками. Тобто треба знати і в «новому» базисі .

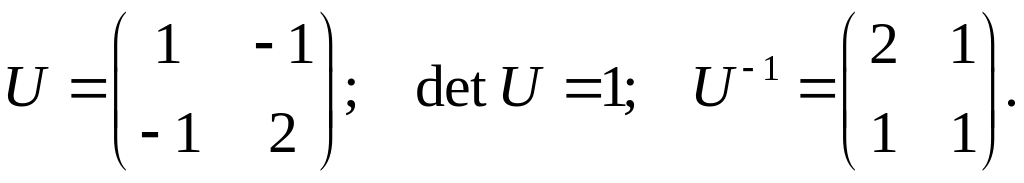
Тоді

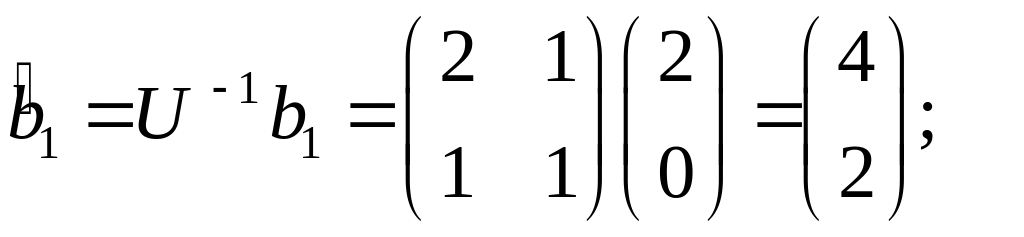
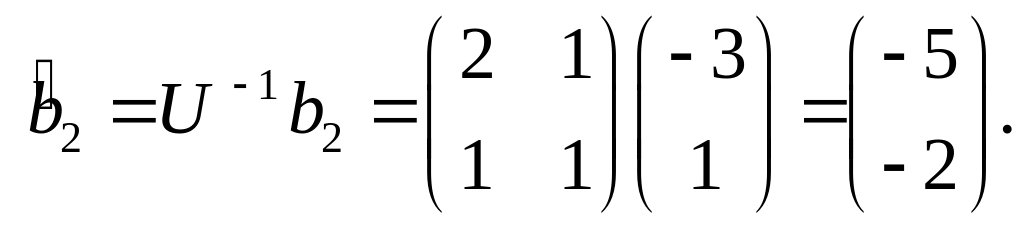
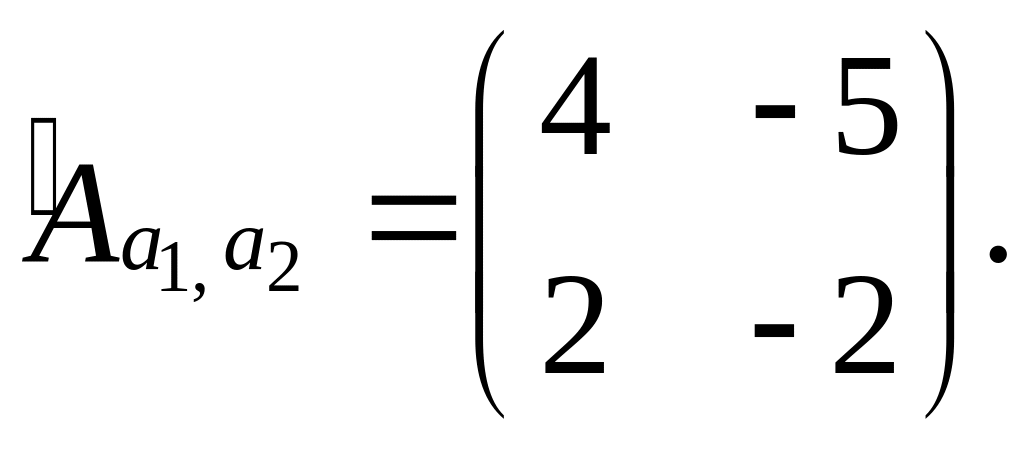
б) В канонічному базисі

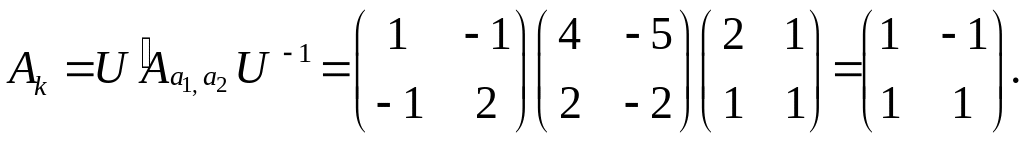
Структура лінійного оператора Власні числа, власні вектори лінійного оператора

Нехай – лінійний оператор, який діє в просторі .

Озн. Вектор називається власним вектором оператора з власним числом , якщо .

Твердження 1. Якщо – власний вектор з власним числом , то ( ) – також власний вектор з тим же власним числом.

.

Якщо до множини векторів ( ) додати нульовий вектор, отримаємо власний лінійний підпростір розмірності .

Твердження 2. Якщо , і , , то – також власний вектор з числом .

.

І знову, якщо до «площини» векторів і додамо нульовий вектор, отримаємо власний підпростір розмірністю .

Ці твердження можна узагальнювати і далі.

Теорема. Якщо – власні вектори оператора , що відповідають різним власним числам , то вони — лінійно незалежні.

; ; ; при .

Доведення. Проведемо доведення за індукцією.

– лінійно незалежний.

Припустимо, що – лінійно незалежні. Лінійну незалежність всіх векторів доведемо від супротивного.

Тобто існують числа , , 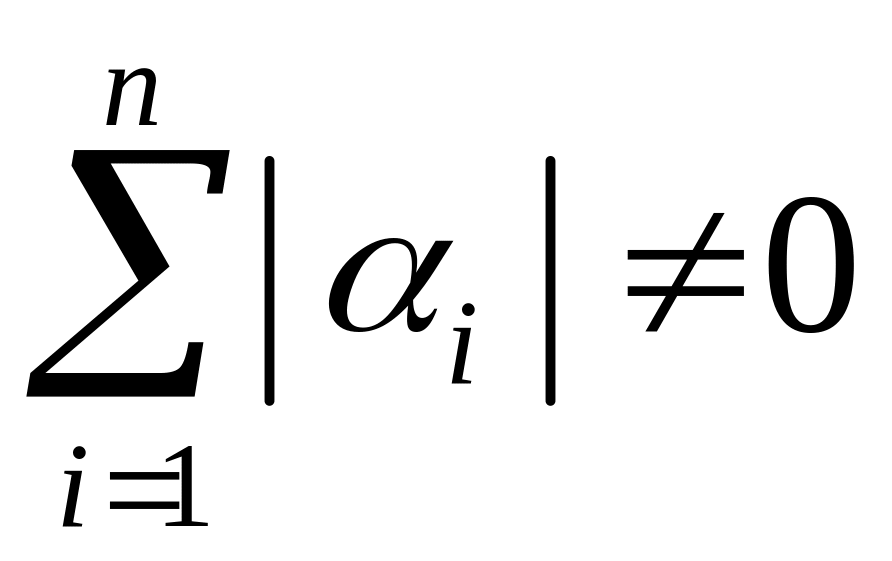такі що

. (1)

Тоді

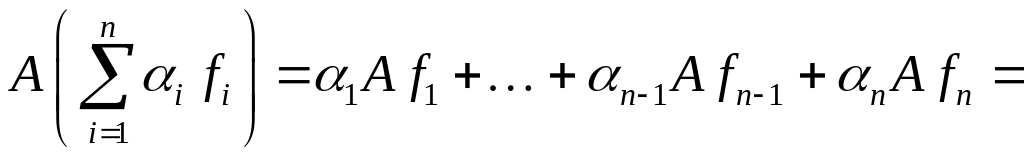
. (2)

Помножимо вираз (1) на і віднімемо від (2). Отримаємо:

.

Для , тому через лінійну незалежність випливає, що .

Але з (1) , що і доводить теорему.

Якщо , та існують лінійно незалежних власних векторів ( , ), то в такому і тільки в такому базисі матриця оператора має діагональний вигляд

.

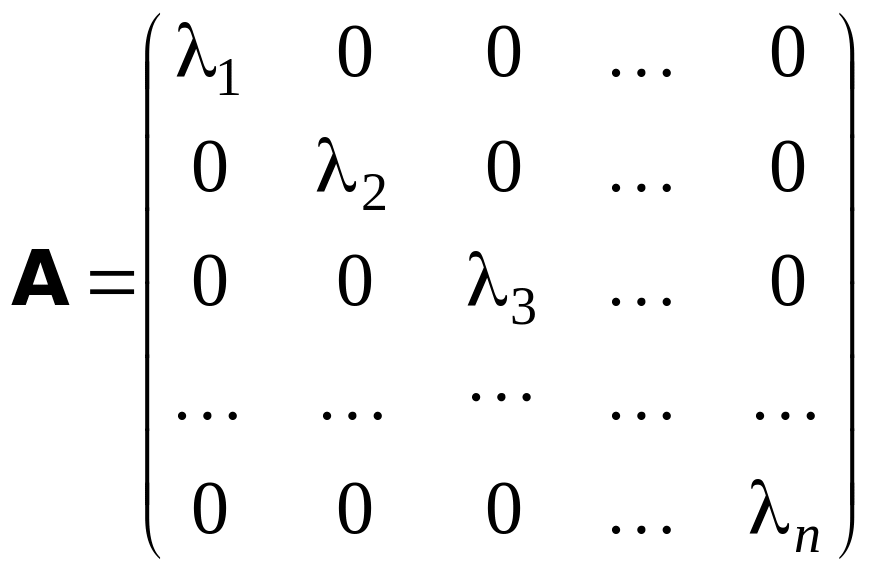Такі оператори називають операторами простої структури.