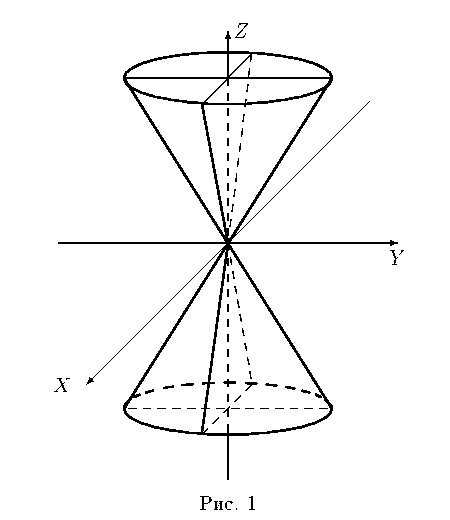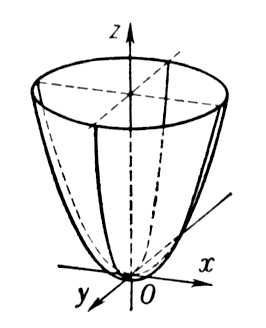
Параболоїд
а) еліптичний
.
Уся
поверхня лежить у верхній частині
простору, бо
.
У перетині
з площинами
маємо еліпси, що збільшуються з ростом
.
А в перетині з
координатними площинами
і
– параболи
і
.
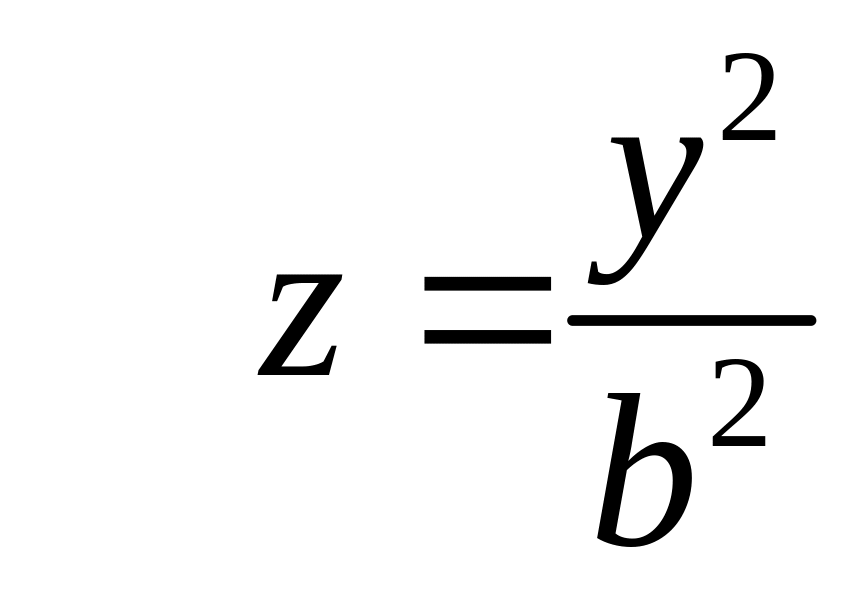Рис. 4 |
б) гіперболічний
.
У перетині
з площиною
маємо параболу
,
а з площиною
–
.
При
у перетині маємо гіперболи
,
а при
– спряжені гіперболи
.
Рис. 5 |
Конус другого порядку
.
Ця поверхня у перетині з площинами утворюють еліпси.
А при
маємо дві прямі:
і
.
При
– прямі
.
Рис. 6 |
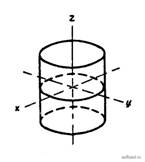
Циліндри другого порядку
а) еліптичний
.
Рис. 7 |
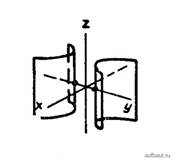
б) гіперболічний
.
Рис. 8 |
в) параболічний
Рис. 9 |
Лінійні простори. Лінійні оператори (продовження)
Сума та перетин лінійних підпросторів
Нехай
– деякий лінійний простір,
–
його підпростори.
Озн
.Сумою
лінійних підпросторів
і
є:
.
Озн
.Перетином
підпросторів
і
є:
.
Твердження. Сума і перетин і є підпросторами .
Доведення.
Нехай
;
;
,
;
;
,
.
Тоді
:
;
.
І нехай
.
Тоді
;
.
Приклади.
а)
Рис. 1 |
|
;
б)
Рис. 2 |
|
;
;
Рис. 3 |
|
Теорема.
.
Доведення.
Нехай
і вектори
– базис
.
Якщо
,
можемо побудувати такий базис
:
.
Аналогічно:
;
– базис
.
Розглянемо систему векторів:
, (*)
і доведемо, що вона є базисом .
;
.
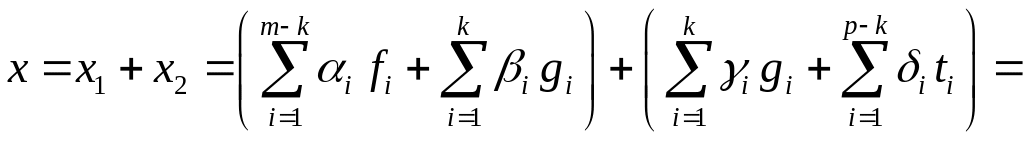
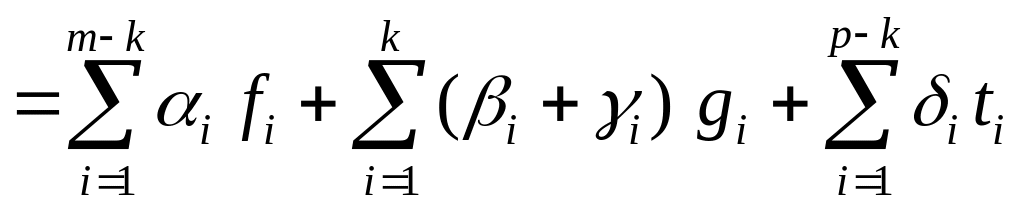Таким
чином, система (*) є повною в
.
Припустимо, що (*) – лінійно залежна,
тобто
,
,
не всі водночас нульові, такі, що
. (1)
Позначимо:
. (2)
Зрозуміло,
що
.
Але із (1)
.
Тобто,
.
Тоді 
. (3)
Із (2) та
(3)
через
лінійну незалежність
.
Маємо
із (1)
з таких же міркувань.
Таким
чином, наше припущення, що у (1) деякі
коефіцієнти
невірне, що й доводить лінійну незалежність
системи (*).
Отримали, що система (*) повна у і лінійно незалежна вона є базисом у .
Кількість
векторів у системі *):
,
що і доводить теорему.
Пряма сума лінійних підпросторів
Нехай
– лінійний простір;
,
.
Озн
. Сума
називається прямою (позначається
),
якщо
;
,
,
і цей розклад єдиний.
Приклади 1) і 2) є прикладами прямої суми, а 3) – ні.
Теорема
2.
Лінійний простір
розкладається у пряму суму своїх
підпросторів
тоді і тільки тоді, коли об’єднання
базисів підпросторів є базисом всього
.
Доведення.
Нехай
,
а
– базис
,
– базис
.
,
;
;
;
,
тобто система векторів
*)
є повною в .
Доведемо, що система *) – лінійно незалежна. Припустимо, що
і
є такі, що
. (1)
Вектор
,
який стоїть праворуч, можна представити
у вигляді
і цей розклад єдиний.
Із (1)
випливає:
,
,
а із
лінійної незалежності базисів
і
:
і
,
що доводить першу частину теореми.
Тепер припустимо, що система *) – базис .
: 
і цей
розклад єдиний. Тобто
,
де
,.
Це і доводить той факт, що сума
– пряма. Теорему доведено.