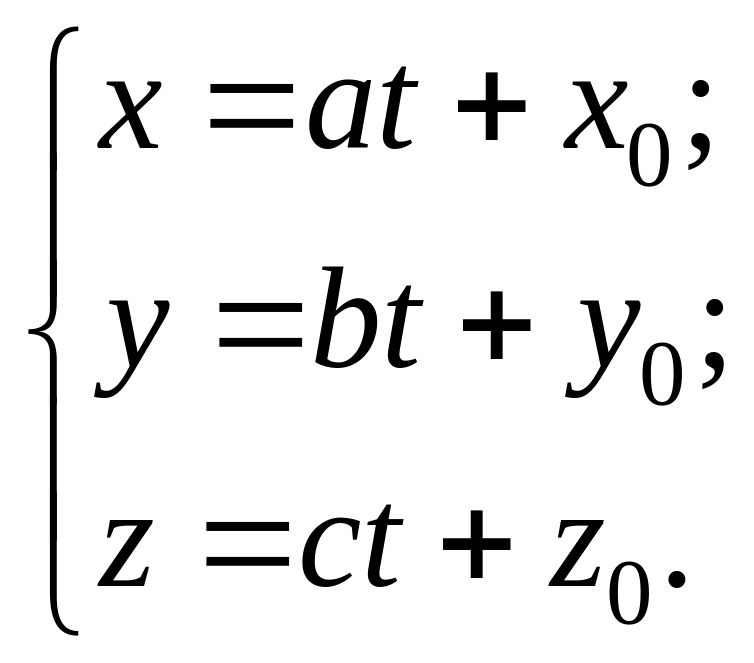61

МІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ

ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

“КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

ФІЗИКО-ТЕХНІЧНИЙ ІНСТИТУТ

А Л Г Е Б Р А ТА Г Е О М Е Т Р І Я - 2

КУРС Л Е К Ц І Й

ДЛЯ СТУДЕНТІВ НАПРЯМІВ ПІДГОТОВКИ

“ПРИКЛАДНА ФІЗИКА”, “ПРИКЛАДНА МАТЕМАТИКА”,

“БЕЗПЕКА ІНФОРМАЦІЙНИХ І КОМУНІКАЦІЙНИХ СИСТЕМ” ТА “СИСТЕМИ ТЕХНІЧНОГО ЗАХИСТУ ІНФОРМАЦІЇ”

Рекомендовано Методичною радою НТУУ “КПІ”

Київ

“ПОЛІТЕХНІКА”

2011

Алгебра та геометрія – 2: курс лекцій для студентів напрямів підготовки “Прикладна фізика”, “Прикладна математика”, “Безпека інформаційних і комунікаційних систем” та “Системи технічного захисту інформації” / Уклад.: Н.Д. Цвинтарна, А.А. Шумська. – К.: НТУУ “КПІ”, 2011. – 62 с.

Гриф надано Методичною радою НТУУ «КПІ»

(Протокол № ____ від _________ 2011 р.)

Н а в ч а л ь н е в и д а н н я

А Л Г Е Б Р А ТА Г Е О М Е Т Р І Я - 2

Курс лекцій

для студентів напрямів підготовки

“Прикладна фізика”, “Прикладна математика”,

“Безпека інформаційних і комунікаційних систем”

та “Системи технічного захисту інформації”

Укладачі: Наталія Дмитрівна Цвинтарна, к.ф.-м. наук, доц.,

Алла Антонівна Шумська, к.ф.-м. наук, доц.

Відповідальний редактор: М.М.Савчук, д.ф.-м.н., проф.

Рецензенти: О.В.Коба, д.ф.-м.н., проф.,

О.М.Фаль, к.ф.-м. наук, доц.

Зміст

Вступ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Аналітична геометрія у просторі

1. Площина у просторі . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2. Пряма у просторі . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3. Поверхні другого порядку . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

ЛІНІЙНА АЛГЕБРА

4. Лінійні простори. Лінійні оператори (продовження) . . . . . . . . . . . 21

   5. Перехід до іншого базису . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . 25

6. Структура лінійного оператора. Власні числа, власні вектори . . . . . 29

7. Жорданова нормальна форма матриці. . . . . . . . . . . . . . . . . . . . . .. . . . 32

8. Функції від матриць. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .. 41

9. Евклідів простір. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

10. Оператори в евклідових (унітарних) просторах. . . . .. . . . . . . .. . . . . .. 51

11. Зведення рівняння поверхні другого порядку до канонічного вигляду55

Список використаної літератури . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

Вступ

Дисципліна “Алгебра та геометрія – 2” є продовженням курсу “Алгебра та геометрія – 1”, який викладається на першому курсі Фізико-технічного інституту для студентів напрямів підготовки “Прикладна фізика”, “Прикладна математика”, “Безпека інформаційних і комунікаційних систем” та “Системи технічного захисту інформації”. Дана дисципліна є базовою для таких дисциплін як математичний аналіз, функціональний аналіз, рівняння математичної фізики та інших.

У цій частині курсу розглядаються такі теми як “Аналітична геометрія у просторі”, “Структура лінійного оператора”, “Евклідові простори та оператори в них”. У кожному розділі у доступній формі розібрано типові задачі, які ілюструють як основні поняття алгебри та геометрії застосовуються до розв’язання задач.

Необхідність електронного курсу лекцій виникла через те, що у другому семестрі за планом маємо аудиторних занять лише “0.5 кредиту”. Цього не вистачає для того, щоб давати всі необхідні доведення теорем, тверджень, детального розбору прикладів.

Укладачі вже використовували деякі частини цього курсу у своїй роботі та отримали позитивні відгуки студентів, щодо такої системи викладання.

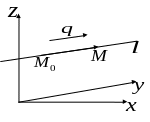
Аналітична геометрія у просторі Площина у просторі

Нехай у просторі задана площина , точка та ; .

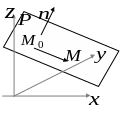
Озн. Вектор називається нормальним вектором площини; задається він єдиним чином з точністю до ненульової константи.

Рис. 1

Нехай т. — довільна точка простору. . Тв. ; . Отримали рівняння площини , яка задана точкою та нормальним вектором. Розкриваючи дужки, маємо: ; — загальне рівняння площини.

Неповні рівняння площини

Виходячи з геометричного тлумачення коефіцієнтів і як координат вектора її нормалі, дослідимо питання про їх вплив на розміщення площини відносно системи координат.

; ;

1) , ,

— площина .

Частковий випадок: — сама площина .

2) ; .

3) ; .

4) і не паралельна жодній координатній площині. Така площина називається площиною загального розташування.

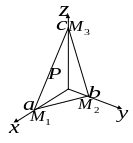
Рівняння площини «у відрізках»

Нехай ; .

; — рівняння площини у відрізках.

Зауважимо, що числа мають простий геометричний зміст: вони дорівнюють величинам відрізків, які відтинає площина на осях і (з урахуванням знаків).

Рис. 2

Справді, якщо дану площину перетнути площинами і , маємо, що точка . Аналогічно , .

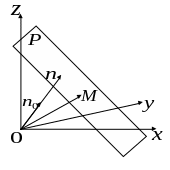
Нормальне рівняння площини

Рис. 3

Нехай площина , що не проходить через , задана так: її нормальний вектор проведено з початку координат в напрямку площини; ; його кути з координатними осями — . ; ; .

Точка — довільна; .

Зрозуміло, що ; або ;

— нормальне рівняння площини.

Щоб звести рівняння до нормального, треба праву і ліву частину помножити на .

Приклад. Звести рівняння площини до нормального виду.

Розв’язання. Нормуючим множником для даного рівняння буде . Знак числа завжди протилежний знаку вільного члена .

.

Відхилення і відстань від точки до площини

Нехай задано площину ; і точку .

.

І нехай — відстань від до .

Озн. Відхиленням від ( позначається ) називається величина

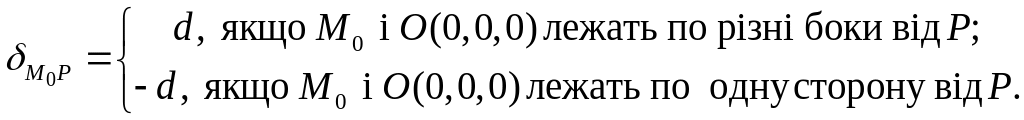
. . Рис. 4

Побудуємо ; . . Враховуючи, що , маємо: ; .

Взаємне розташування площин

; ; .

; ; .

1) Площини і співпадають; .

Тоді .

2) ; .

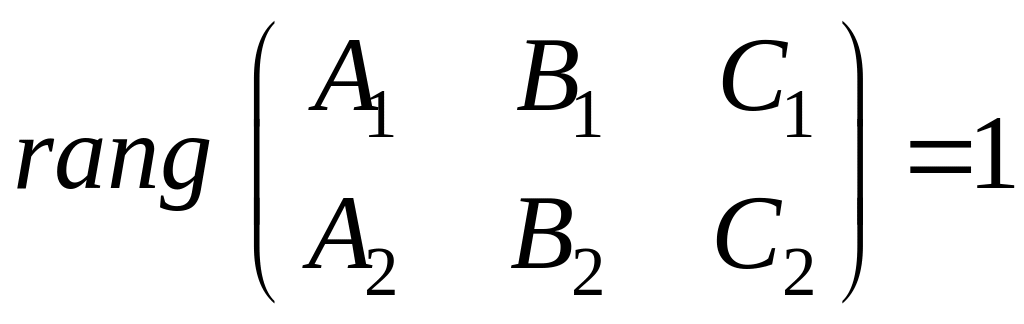Тоді і , а .

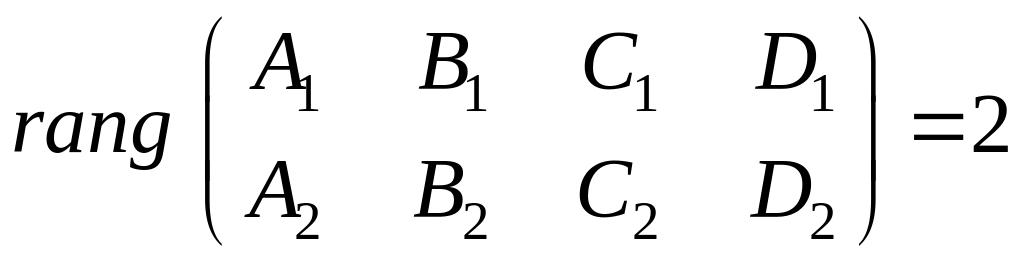Відстань від до доцільно шукати, як відстань від до ;

.

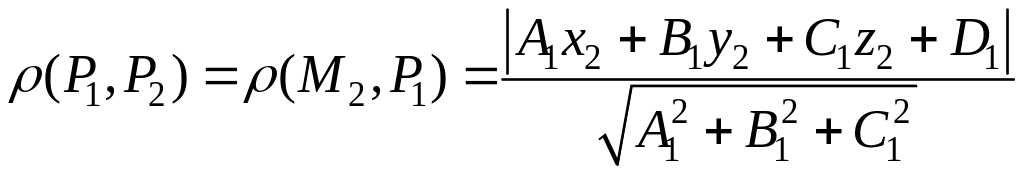3) ╫ ;

╫ .

Якщо , то .

Пряма у просторі

Пряма у просторі задається двома принципово різними способами.

I спосіб. Нехай — пряма; точка ;

Озн . Вектор ; називається напрямним вектором прямої .

Точка — довільна точка простору.

Рис. 5

. Зрозуміло, що або . (1) Ми отримали так зване канонічне рівняння прямої.

Рівняння ; і — рівняння площин, що проектують пряму на координатні площини.

II спосіб. Площини і , ╫ задаються рівняннями:

.

.

Пряму задають як перетин і :

(2)

Для того, щоби звести рівняння прямої типу (2) до вигляду (1), треба знайти напрямний вектор і якусь точку , що належить .

; .

Якщо систему (2) розглядати як неоднорідну систему лінійних рівнянь (за умовою вона сумісна!), то якийсь її частковий розв’язок і дасть нам координати точки .

Як наслідок рівняння прямої типу (1) є її параметричне рівняння:

;