Контрольні запитання та завдання

1

Рис. 2.2 Рис. 2.3

. Поясніть послідовність визначення струмів та їх напрямків в гілках електричного кола за методами контурних струмів, законів Кірхгофа, вузлової напруги та накладання дій ЕРС.

2. Поясніть послідовність визначення струму в гілках електричного кола методом еквівалентного генератора.

3. Указати рівняння, що вірно складені відповідно до першого (другого) закону Кірхгофа для електричного кола, показаного на рисунку на рис. 2.2.

1. –I₁+I₂–I₃–I₄=0; 2. –R₃I₃–R₁I₁ =E₁; 3. R₅I₅+R₁I₁+R₂I₂=E₁+E₂;

4. –I₁–I₃+I₅=0; 5. R₂I₂+R₄I₄= –E₂; 6. –R₃I₃+R₁I₁ =E₁; 7. I₂–I₄=0.

4. До методу накладання дій ЕРС. Визначити значення струму через резистор R₃ від дії джерела з ЕРС Е₁ (або E₂). Параметри електричного кола, що на рис. 2.3, наступні: Е₁=60 В, R₁=30 Ом, Е₂=30 В, R₂=60 Ом, R₃=60 Ом.

5. Визначити струм в резисторі R₃ методом еквівалентного генератора, рис. 2.3. Параметри електричного кола наступні: Е₁=60 В, R₁=30 Ом, Е₂=30 В, R₂=60 Ом, R₃=80 Ом.

До звіту

Рис. 2.4. Формування системи рівнянь та їх розв’язок в середовищі Mathcad.

Рис. 2.5. Дослідження електричного кола: до методу контурних струмів.

Рис. 2.6. Дослідження спрощеного електричного кола: до методу рівнянь Кірхгофа.

Рис. 2.7. Дослідження спрощеного електричного кола: до методу вузлової напруги.

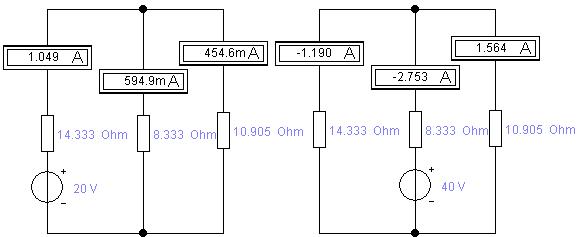
Рис. 2.8. Дослідження спрощеного електричного кола: до методу накладання дій ЕРС.

Рис. 2.9. Дослідження вихідного електричного кола: до методу

еквівалентного генератора.

До звіту

Рис. 2.10. Формування системи рівнянь та їх розв’язок в середовищі Mathcad.

Рис. 2.11. Дослідження електричного кола: до методу контурних струмів.

Рис. 2.12. Дослідження спрощеного електричного кола: до методу рівнянь Кірхгофа.

Рис. 2.13. Дослідження спрощеного електричного кола: до методу вузлової напруги.

Рис. 2.14. Дослідження спрощеного електричного кола: до методу

накладання дій ЕРС.

Рис. 2.15. Дослідження вихідного електричного кола: до методу

еквівалентного генератора.

Додаткові теоретичні відомості

До складних електричних кіл належать розгалужені кола, що мають більше одного джерела енергії. Розраховують їх такими методами:

− метод безпосереднього застосування законів Кірхгофа;

− метод контурних струмів;

− метод вузлових потенціалів (вузлових напруг);

− метод накладання (суперпозиції);

− метод еквівалентного генератора.

Метод безпосереднього застосування законів Кірхгофа є класичним і основним для розрахунку складних електричних кіл, а методи контурних струмів і вузлових потенціалів (вузлових напруг) ґрунтуються на цих фундаментальних законах електротехніки і мета їх використання – зменшення трудомісткості розрахунків. Тому шлях до оволодіння названими методами розрахунку простий і очевидний – це докорінне усвідомлення законів Кірхгофа.

Е

Рис. 2.16

квівалентні перетворення в розрахунках складних електричних кіл застосовують для зменшення кількості віток або вузлів у схемі, що веде до зменшення числа розрахункових рівнянь i скорочення обчислювальної роботи.

Умова еквівалентних перетворень: напруги i струми в не перетворених частинах кола повинні залишатися незмінними. Поширеним методом в розрахунках складних електричних кіл є взаємне еквівалентне перетворення з'єднань споживачів енергії "трикутником" i "зіркою", рис. 2.16.

Формули перетворення з’єднання "трикутника" на "зірку":

, , .

Обернене перетворення виконується за формулами:

, , .

На принципі еквівалентності ґрунтується метод еквівалентного генератора, який доцільно застосовувати в тому разі, коли потрібно розрахувати струм тільки в одній вітці електричного кола. Метод базується на теоремі Тевенена про еквівалентний генератор або активний двополюсник. Під активним двополюсником розуміють частину кола, що містить джерела енергії i з’єднується з іншими елементами кола двома затискачами, рис. 2.17.

Згідно з теоремою, струм у вітці, що ввімкнена на затискачі 1-2, залишається незмінним, якщо активний двополюсник замінити еквівалентним генератором з ЕРС Е_ekb i його внутрішнім опором R_ekb, рис. 2.17. Значення Е_ekb обчислюється як напруга U₁₂ на затискачах 1-2 в режимі холостого ходу, тобто коли вилучена вітка з опором R, у якій потрібно знайти струм., Е_ekb= U₁₂. Напругу U₁₂ на затискачах 1-2 можна визначити будь-яким методом.

З

Рис. 2.17

начення R_ekb розраховується як еквівалентний опір двополюсника відносно затискачів 1-2 у тому ж режимі холостого ходу за умови, що активний двополюсник стане пасивним, тобто значення його джерел потрібно вважати рівними нулю.

Після визначення параметрів еквівалентного генератора приєднуємо вітку, у якій потрібно визначити струм і визначаємо цей струм за законом Ома.

Параметри еквівалентного генератора можна визначити за режимами холостого ходу та короткого замикання: вимірюються значення напруги в режимі холостого ходу U₁₂ і значення струму, що протікає через клеми двополюсника при їх короткому замиканні, I_кз. Тоді значення Е_ekb визначається як напруга U₁₂, а еквівалентний опір R_ekb між затискачами 1 i 2 буде: R_ekb = U₁₂/ I_кз.

Зауваження: на загал гілка, в котрій потрібно обчислити струм, може включати також джерело напруги або з’єднувати довільну частину електричного кола.

Під час проектування та експлуатації електричних пристроїв важливо знати різницю потенціалів між відповідними вузлами схеми електричного кола, тому що елементи кола, що приєднані до вузлів що мають велику різницю потенціалів,мають бути розташовані на достатній відстані, щоб запобігти пробою ізоляції між ними. Це особливо важливо в разі обмеження габаритів електротехнічного пристрою.

В

Рис. 2.18

изначити різницю потенціалів між відповідними вузлами чи точками електричної схеми зручно за допомогою потенціальної діаграми, яка представляє графік розподілу потенціалу вздовж будь-якого шляху у електричному колі, наприклад, контурі. У декартовій системі координат за віссю абсцис відкладають значення опорів резисторів, що входять до складу контуру, дотримуючись послідовності їх увімкнення у схемі, а за віссю ординат – потенціали відповідних точок кола.

Масштаб за віссю абсцис визначають, зважаючи на сумарний опір резисторів, що складають контур, а за віссю ординат зважаючи на екстремальні значення потенціалів. Побудовані точки відповідно до потенціалів з’єднують прямими лініями. Кут нахилу кожного з відрізків до горизонтальної осі визначає значення струму через ділянку кола.

Побудуємо таку діаграму для контуру, рис. 2.18: R₅=10 Ом, E₂=40 В, R₂=5 Ом, Е₁=20 Ом, R₁=13 Ом ,R₆=4 Ом, R₅=10 Ом, І₁=0.14 А, І₂=2.159 А, І₅=1.104 А, І₆=0.914 А.

Для цього потенціал будь-якої точки контуру, наприклад, 4 приймаємо за нульовий, а потенціали інших визначаємо відповідно до нього. Попередньо задамося напрямком обходу контуру. Якщо струм в гілці збігається з напрямком обходу контуру, то потенціал наступної точки контуру зменшується на величину спаду напруги на опорі резистора, який розділяє ці точки. Якщо ж між точками знаходиться джерело ЕРС, то потенціал наступної точки збільшиться на її величину коли напрям дії ЕРС збігається з напрямом обходу.

Розрахунок потенціалів точок контуру показаний дальші і побудова потенціальної діаграми виконана в середовищі Mathcad, рис. 2.19.

Рис. 2.19

23