Прогнозирование с помощью функции "предсказ"

ЗАДАЧА 7. Имеются данные зависимости У от X. Необ­ходимо получить прогнозное значение У по линейной модели с использованием функции "ПРЕДСКАЗ".

Решение.

1. Введите данные в таблицу. Скопируйте весь лист, в кото­ром решалась задача 1.

2. Назначьте ячейку, в которой будет находиться ожидаемое значение X. Например, в ячейке А12 будет находиться ожидаемое значение X.

3. Введите в ячейку А 12 ожидаемое значение, равное 11.

4. Назначьте ячейку, в которой будет находиться прогнозное значение У, вычисленное по линейной модели. Например, в ячейке В12 будет прогнозное значение У.

5. В ячейку В12 введите функцию "ПРЕДСКАЗ". Поставьте в ячейку В12 " = ", щелкните по пиктограмме "Вставка функции", выберите категорию "Статистические", выберите функ­цию "ПРЕДСКАЗ", на экране должно появиться изображение, представленное на рис. 7.16, нажмите на знак "?" и прочтите описание этой функции.

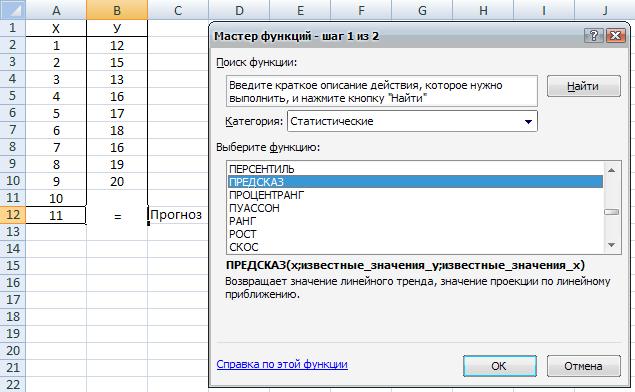
Рис. 7.16. Выбор функции "ПРЕДСКЛЗ"

6. Получите прогнозное значение У по линейной модели. Нажмите на кнопку "ОК" и введите пара метры функции "ПРЕД­СКАЗ", представленные на рис. 7.17. Нажмите кнопку "ОК" и получите в ячейке В12 прогнозное значение, вычисленное по линейной функции.

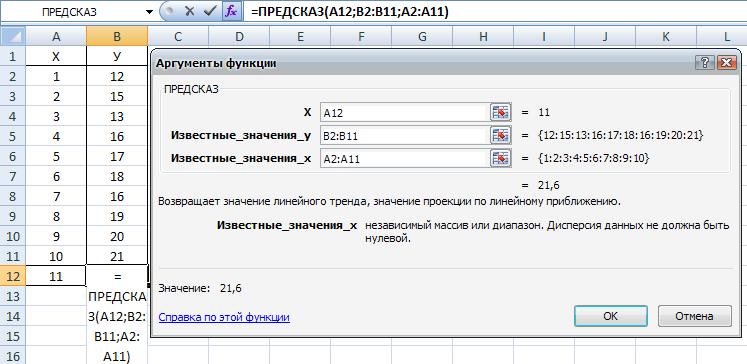
Рис. 7.17. Параметры функции "ПРЕДСКАЗ"

7. Сравните полученный прогноз с предыдущими прогноз­ными значениями, вычисленными с использованием других инструментальных средств.

Прогнозирование оптимального распределения бюджета предприятия

Продемонстрируем совместное использование изученных инструментальных средств прогнозирования "ПРЕДСКАЗ", "ЛИНЕЙН", "Поиск решения" при решении прикладных задач на примере прогнозирования оптимального распределения бюд­жета предприятия на 2008 г.

ЗАДАЧА 8. Имеется база данных статей бюджета (X1, ..., Х7) и основных показателей деятельности предприятия (У 1, У2), представленная в табл. 7.2.

Таблица 7.2

Год	X1	Х2	ХЗ	Х4	Х5	Х6	Х7	У1	У2
1999	3,6	0,4	0,2	0,4	2,3	1,4	1,5	9,8	2
2000	5,6	0,8	0,3	0,5	3,1	1,6	0,5	12,4	3,2
2001	4,4	1	0,5	0,6	2,9	1,7	3,3	14,4	4,1
2002	4,8	1,2	0,8	0,7	3	1,8	1,5	13,8	4,2
2003	5,1	1,4	0,9	0,8	4,1	1,9	2,6	16,8	5,9
2004	5,8	1,9	1,1	0,9	4,2	2	0,3	16,2	5,1
2005	8	2,4	1,4	1,8	5,7	2,8	1	23,1	8,2
2006	9,1	2,8	1,8	1,8	6,2	3	2,2	26,9	9,1
2007	8,5	3,8	1,9	1,9	7,4	3,2	1,9	28,6	10,2
2008	?	?	?	?	?	?	?	?	?

где год — время анализа данных;

X1 — средства на развитие основного производства (млн руб.);

Х2 — средства на развитие вспомогательного производства (млн руб.);

ХЗ — средства на виды обеспечения производства (млн руб);

Х4 — средства на совершенствование управления производством (млн руб.);

Х5 — средства на создание резерва материалов и комплектующих, на развитие инфраструктуры, на капитальное строи­тельство (млн руб.);

Х6 — фонд заработной платы (млн руб.);

Х7 — резервы финансовых средств (млн руб.);

У1 — доходы предприятия (млн руб.);

У2 — прибыль предприятия (млн руб.).

Введем основные соотношения между переменными:

1. Доходы предприятия (У1) должны равняться расходам (XI, ..., Х7) за каждый текущий год:

X1 + Х2 + ХЗ + Х4 + Х5 + Х6 + Х7 = У1.

2. Средства на развитие основного и вспомогательного производства (X1, Х2) должны составлять не менее 40% от доходов предприятия (У1):

(X1 +Х2) > = 0,4 У1.

3. Средства на развитие основного производства (XI) долж­ны быть не менее средств на развитие вспомогательного произ­водства (Х2):

X1 = Х2.

4. Средства на виды обеспечения и совершенствование управления производством (ХЗ, Х4) должны составлять не более 15% от суммы средств затрат на развитие основного и вспомогательного производства (X1, Х2):

(ХЗ + Х4) < = 0,15(Х1 + Х2).

5. Фонд заработной платы (Х6) должен быть не менее 1,5 млн руб.

Х6 > = 1,5.

6. Размер статей бюджета (X1, ..., Х7) должен быть не менее нуля.

Х1> = О, Х2> = О, Х3> = О, Х4> = О, Х5> = 0, Х6> = О, Х7> = 0.

7. Прибыль (У2) предприятия линейно зависит от значений статей бюджета (Х1, …, Х7):

У2 = а0 + а1*Х1 + а2*Х2 + а3*Х3 + а4*Х4 + а5*Х5 + а6*Х6 + а*Х7.

Необходимо:

1. Получить прогнозные значения повеем статьям бюджета (Х1пр, ..., Х7пр) доходов (У1пр) и прибыл и (У2пр) предприятия на 2008 г.

2. Получить прогнозный оптимальный план распределения прогнозного значения доходов (У 1пр) по статьям бюджета (X1оп, .... Х7оп) предприятия на 2008 г., при условии получения максимальной прибыли (У2оп) и соблюдения основных соотношений (ограничений) между переменными.

Решение.

1. Получите прогнозные значения по всем статьям бюджета (Х1пр, .... Х7пр) доходов (У1пр) и прибыли (У2пр) предприятия на 2008 г.

А. Введите исходные данные. Загрузите "Excel", перейдите на чистый лист, введите базу данных, представленную в табл. 7.2

Б. Получите прогнозные значения для всех переменных (Х1пр,..., Х7пр, У1пр, У2пр) на 2008 г. с помощью функции "ПРЕДCКАЗ". Образец решения см. на рис. 7. 18.

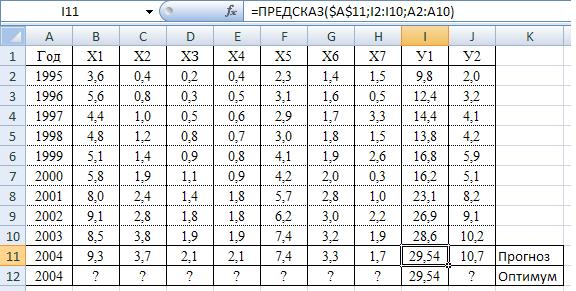
Рис. 7.18. Получение прогнозов для всех переменных на 2008 г. с помощью функции "ПРЕДСКАЗ"

Полученные прогнозные значения статей бюджета на 2008 г. можно рассматривать как первоначальный план бюджета, но он не является оптимальным, так как при их расчетах не учитыва­лись ограничения их значения. Например, прогнозное значение доходов У1пр — 29,5 млн руб. должно равняться сумме всех статей расходов Х1пр + Х2пр + Х3пр + Х4пр + Х5пр + Х6пр + Х7пр = 9,3 + 3,7 + 2,1 + 2,1 + 7,4 + 3,3 + + 1,7 = 29,5 млн. руб. В данном случае доходы и расходы совпадают с точностью до десятых долей, однако данное совпадение скорее случайность, чем закономерность, так как это ограничение не учитывалось в прогнозах доходов и расходов. При желании можно проверить остальные ограничения на переменные, изложенные в условии задачи.

Прогнозное значение прибыли У2пр — 10,7, очевидно, не является оптимальным, так как в прогнозных расчетах не учи­тывалась максимизация его значения.

2. Получите прогнозный оптимальный план распределения прогнозного значения доходов (У1пр) по статьям бюджета (Х1оп, ...,Х7оп) предприятия на 2008 г., при условии получения мак­симальной прибыли У2оп и соблюдения основных соотношений (ограничений) между переменными.

• Вычислите коэффициенты целевой функции, которую следует максимизировать.

По имеющейся базе данных с помощью функции "ЛИНЕЙН" определите коэффициенты линейной модели зависимости при­были (У2) предприятия от статей бюджета (X1, ..., Х7):

У2 = а0 + а1*Х1 + а2*Х2 + а3*Х3 + а4*Х4 + а5*Х5 + а6*Х6 + а*Х7

Образец решения см. на рис. 7.19.

При этом следует учесть следующие особенности расчетов по функции "ЛИНЕЙН":

— зависимой переменной является У2, объясняемыми пе­ременными являются XI, ..., Х7;

• протокол расчетов по функции "ЛИНЕЙН" имеет 8 столбцов и 5 строчек;

• для распространения расчетов с одной ячейки на весь массив протокола расчетов необходимо выделить первую ячейку с расчетами и дополнительно справа 7 столбцов и вниз 4 строчки, нажать и отпустить клавишу "F2", последовательно, не отпуская, нажать па клавиши "Ctrl", "Shift", "Enter", затем отпустить все клавиши.

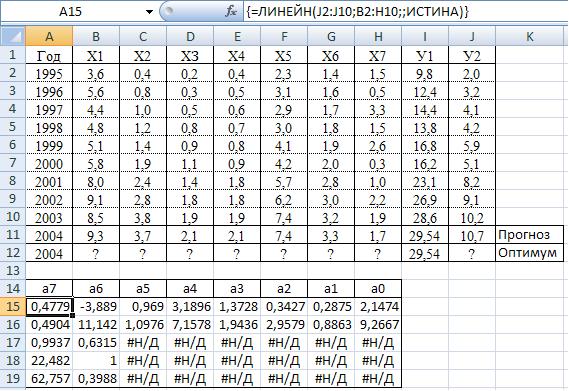
Рис. 7.19. Расчет коэффициентов многофакторной модели

с помощью функции "ЛИНЕЙН"

Линейная многофакторная модель зависимости У2 от X1, ..., Х7 имеет следующий вид:

У2 = 2,1474 + 0,2875*Х1 + 0,3427*Х2 + 1,3728*ХЗ + 3,1896*Х4 + + 0,969*Х5 - 3,889*Х6 + 0,4779*Х7.

Обратите внимание на то, что коэффициент перед Х6 имеет отрицательный знак. Это означает, что увеличение фонда заработной платы приводит к снижению прибыли предприятия.

Полученное математическое выражение зависимости У2 от X1,.... Х7 является целевой функцией, которую надо максимизировать. Для этого надо подобрать такие значения X1, Х2, Х5, Х4, Х5, Х6, Х7, при которых целевая функция (У2) будет иметь максимальное значение, при условии соблюдения ограничений, накладываемые на искомые значения переменных. Подобные задачи решаются с помощью программы "Поиск решения".

• Выполните подготовительные действия. Для реализации программы "Поиск решения" необходимо произвести следующие подготовительные действия.

- выделите ячейки В22, С22, D22, Е22, F22, G22, Н22, в которых будут находиться искомые переменные X1, ..., Х7 соответственно;

- в ячейку I22 введите значение Упр1;

- в диапазон ячеек А25: С28 введите ограничения и целе­вую функцию. Результаты выполнения задания представлены на рис. 7.20 и 7.21, где изображены содержимое ячеек и их зна­чения.

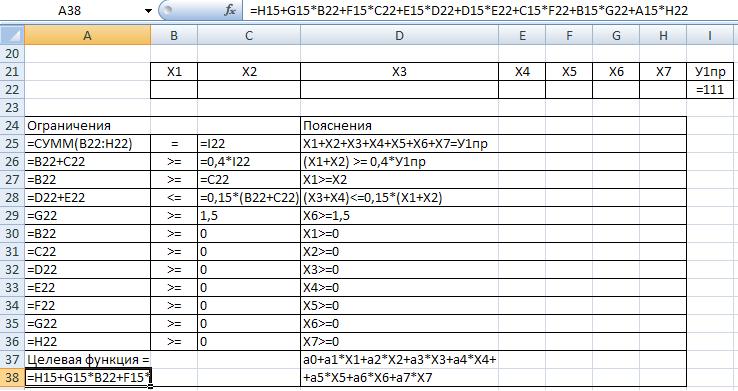
Рис. 7.20. Результат подготовительных действий перед выполнением программы "Поиск решения". Содержимое ячеек

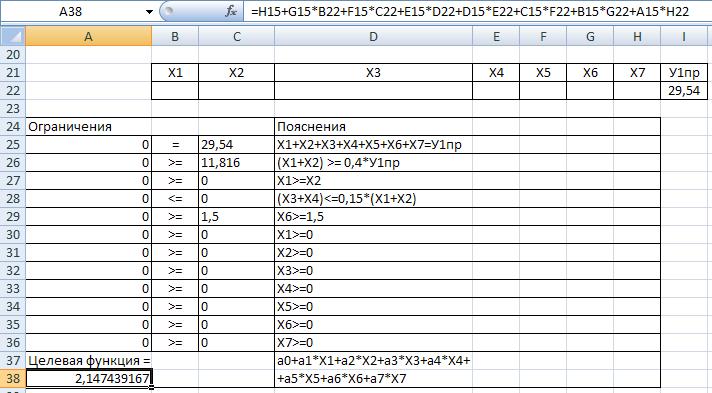
Рис. 7.21. результат подготовительных действий перед выполнением программы "Поиск решения". Значения ячеек

• Получите решение по программе "Поиск решения". Обратитесь к программе "Поиск решения", введите все необходимые параметры и получите решение. На рис. 7.22 изображены значения параметров программы "Поиск решения", где ограничения записаны в следующем виде: значение целевой функции (У2оп) находится в ячейке А38.

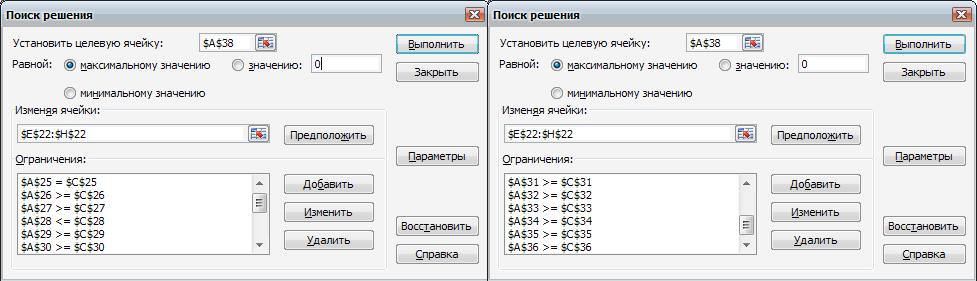
Рис. 7.22. Значения параметров программы "Поиск решения"

Результат расчетов по программе "Поиск решения" изображен на рис. 7.23.

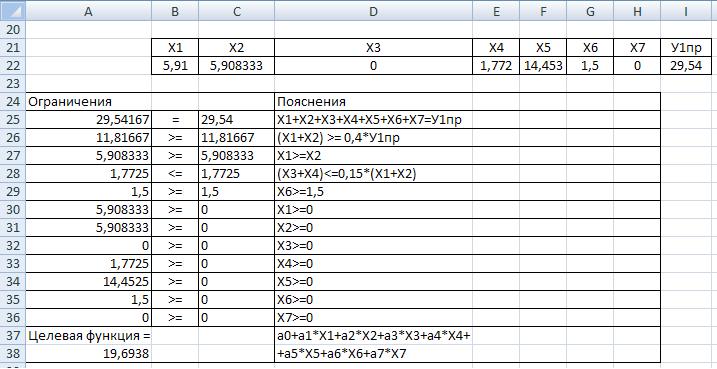
Рис. 7.23. Результат расчетов по программе "Поиск решения"

• Введите найденные значения Х1оп, …,Х7оп и У2оп и У1пр в исходную таблицу.

• Результат процесса изображен на рис. 7.24.

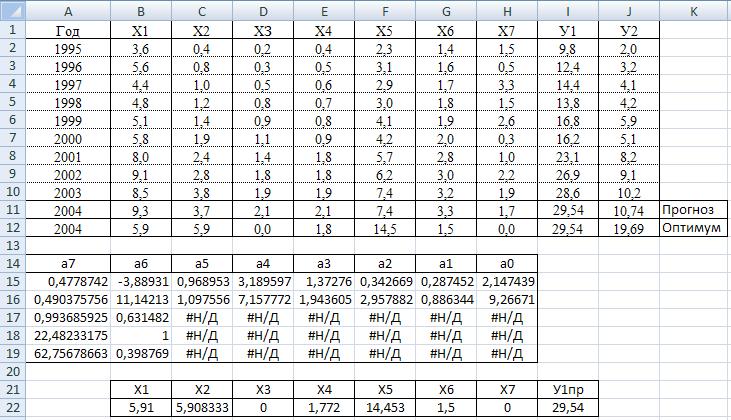
Рис. 7.24. Результат решения задачи

• Проведите анализ полученного решения. Сравнение распределении средств по статьям бюджета, выполненного по прогнозу и по оптимальным значениям, показывает их существенное различие по отдельным статьям, таким как: ХЗ, Х5, Х6, Х7. В оптимальном варианте по статьям ХЗ и Х7 не выделено средств. Оптимальное значение прибыли У2оп = 19,694 больше, чем по прогнозу У2пр = 10,7. Однако в оптимальном варианте распре­ деления бюджета учтены все ограничения на значения Х1оп, ..., Х7оп, У1пр. Если есть время, то проверьте самостоятельно эти ограничения.

• Выделите средства по всем статьям бюджета. Решение задачи по оптимальному варианту нельзя признать оконча­ тельным, так как по статьям бюджета Х3оп и Х7оп не выделено средств. Необходимо самостоятельно исправить ограничения для переменных ХЗ, Х7 и выделить для них минимальное необходи­мое значение (допустим Х3 >= 1, Х7 >= 1). Затем пересчитать оптимальный план, при этом целевая функция (прибыль У2оп) должна снизить свое значение. Окончательный вариант оптимального распределения бюджета изображен на рис. 7.25.

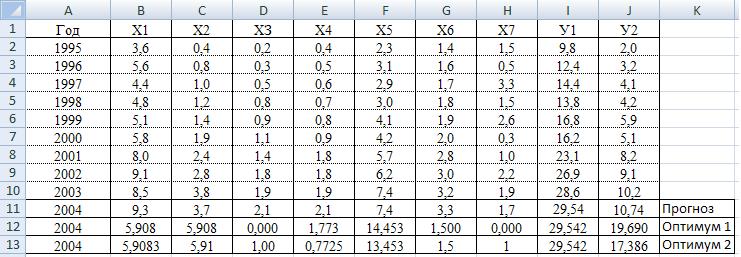
Рис. 7.25. Варианты оптимальных распределений бюджета при различных ограничениях

Анализ рис. 7.25 показывает, что в оптимальном варианте 2 по всем статьям бюджета выделены средства, однако по срав­нению с предыдущим вариантом 1 оптимального распределения бюджета значение целевой функции (прибыль У2оп) уменьши­лось с 19,694 млн руб. до 17,386 млн руб.