Прогнозирование с помощью пакета программ ''анализ данных"

3АДАЧА 5. Имеются данные зависимости У от X. Необходимо получить прогноз значения У по линейной модели с ис­пользованием программы "Регрессия", которая входит в состав пакета программ "Анализ данных".

Решение.

Для прогнозирования можно использовать программу '"Рег­рессия".

1. Прочтите в справочной системе "Ехсеl" описание про­граммы "Регрессия". Найдите описание программы "Регрессия" по следующему пути: "?", "Вызов справки", "Содержание", "Статистический анализ", "Регрессия". К сожалению, в справке имеется только описание меню программы, но нет описания расчетных формул этой программы. Для подробного ознакомления с алгоритмами расчетных формул необходимо обратиться к учебникам по эконометрике.

2. Введите данные в таблицу. Скопируйте весь лист, в кото­ром решалась задача 1.

3. Выполните программу "Регрессия". Щелкните кноп­ку "Сервис", выберите пункт ''Анализ данных", выберите программу "Регрессия", нажмите кнопку "ОК", на экране появится окно программы 'Регрессия , заполните параметры программы в соответствии с рис. 7.12, нажмите кнопку "ОК". На экране появится протокол расчетов, изображенный на рис. 7.13.

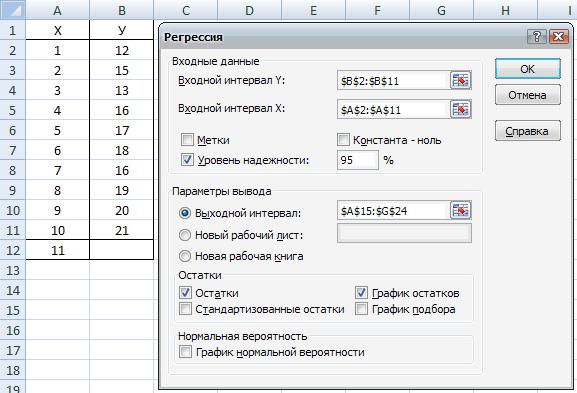
Риc. 7.12. Параметры программы "Регрессия"

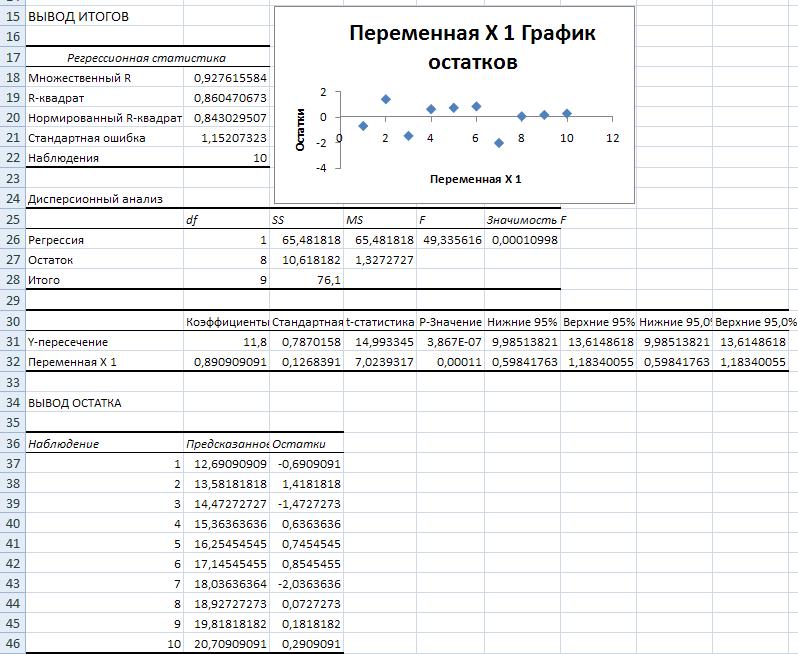
Рис. 7.13. Вывод результатов расчетов по программе "Регрессия"

4. Проведите анализ расчетов. Найдите в протоколе расче­тов "Регрессия" значения коэффициентов а0 и а1 и сравните их значения с протоколом расчетом функции " ЛИНЕЙН". Найдите в протоколе расчетов "Регрессия" "Предсказанное значение У" и сравните их значениями Ур, представленных на рис. 7.4. Найдите в протоколе расчетов "Регрессия" значение критерия Фишера и сделайте вывод о достоверности линейной модели (если значи­мость критерия Фишера будет меньше 0,05, то модель является достоверной. Более подробно о характеристиках модели читайте в курсе "Эконометрика").

5. Получите прогнозное значение У на 2008 г. при X = 11. Значения а0 и а1 можно взять из протокола расчетов программы "Регрессия".

Прогнозирование с использованием программы "поиск решения"

Определение коэффициентов любого уравнения регрессии можно представить как оптимизационный процесс по миними­зации целевой функции методом линейного программирования, предложенный Канторовичем. Программа "Поиск решения" позволяет итерационным методом определить коэффициенты любого уравнения регрессии, если в качестве целевой функции выбрать сумму квадратов остатков. Под остатком понимается разность между фактическим и расчетным значением зависи­мой переменной.

3АДАЧА 6. Имеются данные зависимости У от Х. Вычислить коэффициенты линейной модели методом наименьших квадра­тов остатков с помощью программы "Поиск решения". Проверить полученные значения коэффициентов на оптимальность. Полу­чить прогнозные значения У по линейной модели.

Решение.

Сущность метода наименьших квадратов. Необходимо найти такие значения коэффициентов а0 и а1 линейной модели У = а0 + а1 • X + е = Ур + с, при которых сумма квадратов (остатков) отклонений е = У - Ур будет минимальной, где Ур = а0 + а1 • X. Расчет коэффициентов а0 и а1 можно вы­полнить разными способами, один из которых предполагает использовать итеративную программу "Поиск решения". Итеративными называют алгоритмы, которые осуществляют поиск решения с помощью последовательных приближений, или итераций.

1. Введите данные в таблицу. Скопируйте весь лист, в котором решалась задача 1.

2. Назначьте ячейки для коэффициентов а0 и а1. Назначьте ячейки В14 и В15 для коэффициентов, соответственно а0 и а1 линейной модели Ур = а0 + а1*Х. Первоначально в этих ячейках значения должны отсутствовать. В дальнейшем в них будет занесен результат выполнения программы "Поиск Решения".

3. В ячейки С2:С11 введите результат расчетов по формуле Ур = а0 + а1*Х. В качестве значений а0 и а1 необходимо взять ячейки соответственно В14 и В15, значения X надо последовательно выбирать из массива А2:А11. Например, в ячейке С2 должна быть введена следующая формула = $В$14 + $В$15*А2, в ячейке СЗ должна быть введена формула = $В$14 + $15$* АЗ и так далее. Подробное описание расчетов Ур смотрите в задаче 1. Так как первоначально значения а0 и а1 равны нулю, то и все значения Ур тоже будут равны нулю.

4. Введите в массив ячеек D2:D11 квадраты остатков (e²). Квадраты остатков вычисляются по формуле (У - Ур)². Например, в ячейке D2 должна быть введена следующая формула: = (B2-C2)^2.

5. Введите целевую функцию. В ячейку С17 ввести целевую функцию, которая будет равна сумме квадратов остатков, т.е. сумма ячеек массива D2:D11. Например, в ячейке С17 должна быть введена формула

= D2 +D3 +D4 +D5 + D6 +D7 +D8 + D9 + D10 + D11.

Все подготовительные операции произведены, теперь необходимо так изменять численные значения а0 и а1, чтобы значение целевой функции было минимальным. Эту процедуру выполнит программа "Поиск решения".

6. Выполните программу "Поиск решения". Нажмите кнопку "Сервис", выберите пункт "Поиск решения", на экране появится окно меню программы "Поиск решения", заполните параметры программы в соответствии с рис. 7.14. Нажмите кнопку "Выполнить" и получите результат, представленный на рис. 7. 1 5.

7. Проведите анализ полученных расчетов. Анализ результатов расчетов показывает, что коэффициенты линейной модели, найденные с помощью функции "Поиск решения", совпадают со значениями соответствующих коэффициентов, определенные с помощью функции "ЛИНЕЙН".

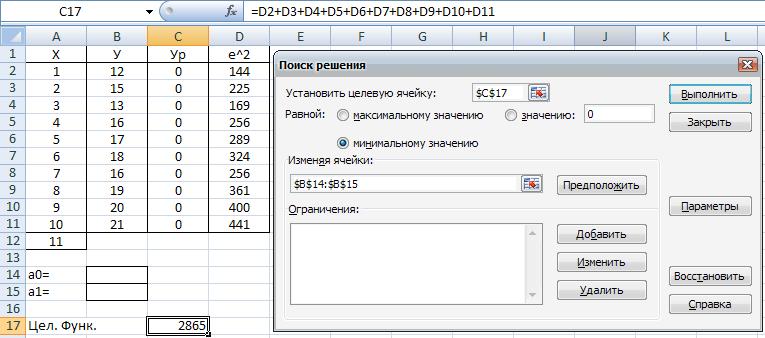
Рис. 7.14. Параметры программы "Поиск решения"

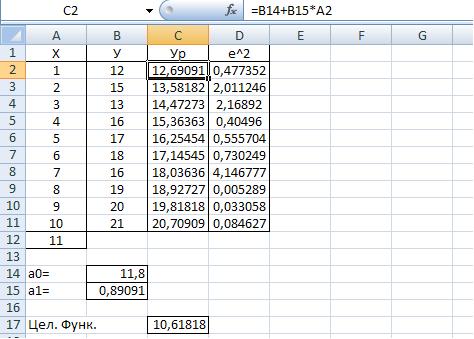
Рис. 7.15. Результат расчета коэффициентов линейной модели с помощью программы "Поиск решения"

8. Проверьте найденные численные значения коэффициентов на оптимальность. Построите график зависимости У и Ур = а0 + а1*Х от X. Измените оптимальные значения коэффи­циентов а0 и а1 в ячейках В14 и В15 и наблюдайте за тем, как изменяются численные значении целевой функции в ячейке С17, а также изучите поведение графика Ур = а0 + а1*Х от­носительно фактических значений У. Убедитесь в том, что при любом изменении оптимальных значений коэффициентов а0 и а1 значение целевой функции возрастает, а график Ур оптимальным образом воспроизводит тенденцию зависимости У от X. Следовательно, найденные значения коэффициентов являются оптимальными.

9. Получите прогнозное значение У на 2008 г. при X = 11.

10. Сравните результаты расчетов с рис. 7.4.