БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОЙ ФИЗИКИ
ВИКТОР АХРАМЕНКО
Математический анализ.
Практические занятия. 2 семестр.
Методическое пособие по практическим занятиям для студентов первого курса
МИНСК
2012
Тема 1. Несобственные интегралы.
Пусть
функция
определена
и интегрируема на отрезке
.
def.
Предел
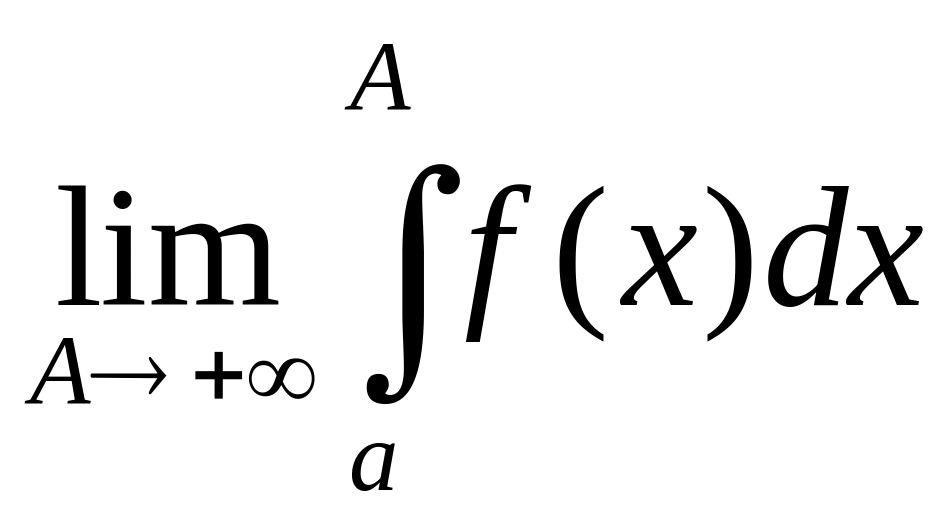называют
несобственным интегралом от функции
на бесконечном промежутке
,
или несобственным
интегралом первого рода
(НИ-1)
и обозначают
.
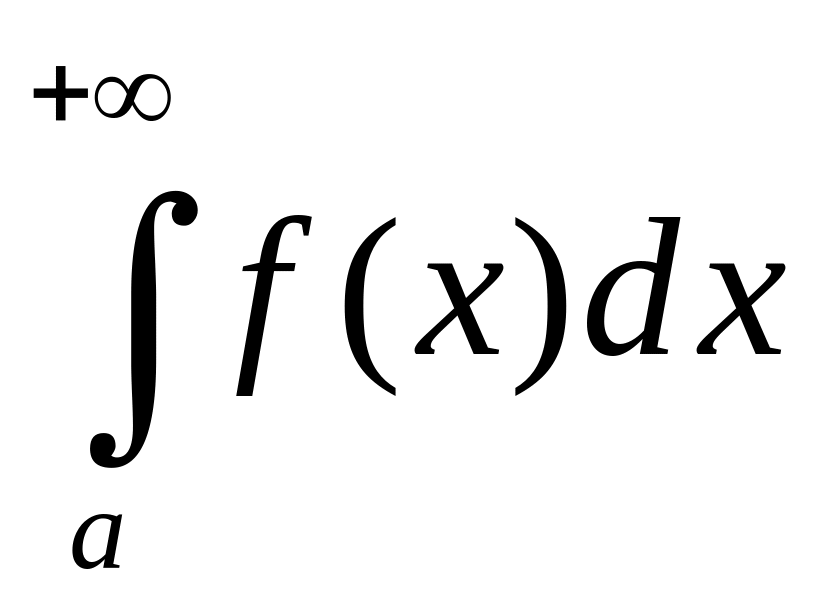
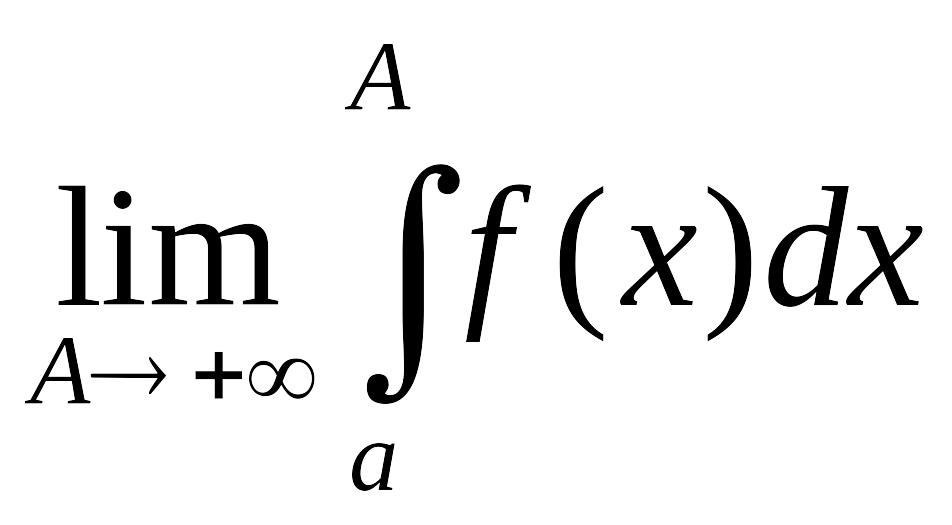(1)
Если
существует конечный предел (1),
то НИ-1 называется сходящимся,
а функция
– интегрируемой
в несобственном смысленсе
на промежутке
.
Если же предел (1)
не существует, то НИ-1 называется
расходящимся,
а если он при этом является бесконечно
большим, то пишут
.
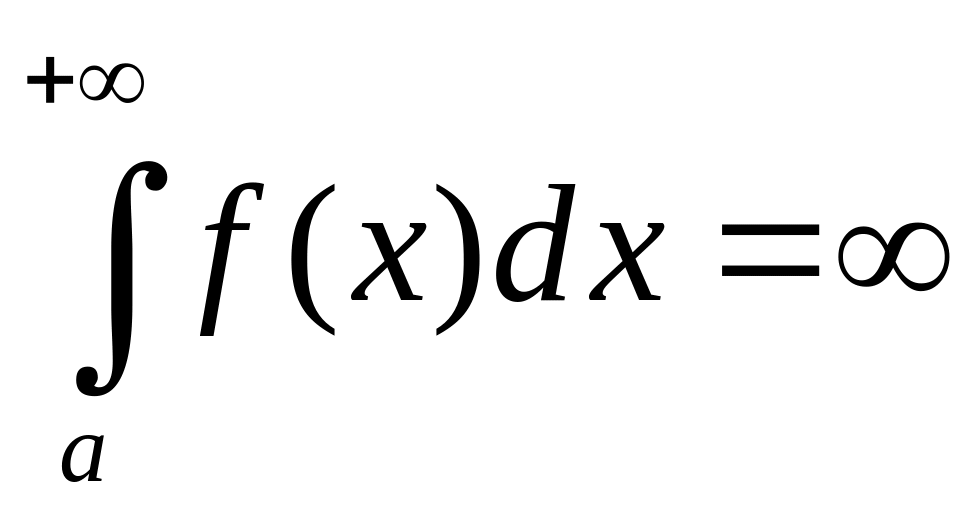Критерий Коши (сходимости НИ-1). Для того чтобы НИ-1 был сходящимся, необходимо и достаточно, чтобы
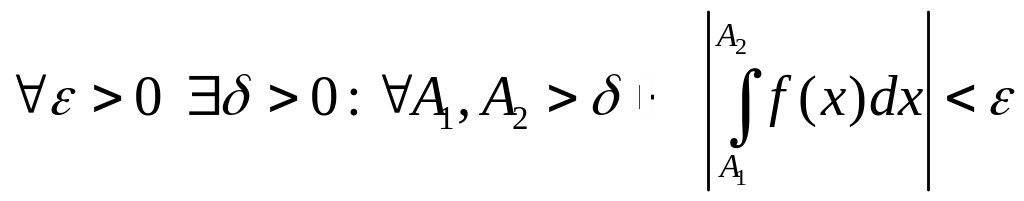
Теорема 1
(признак сравнения).
Если
и
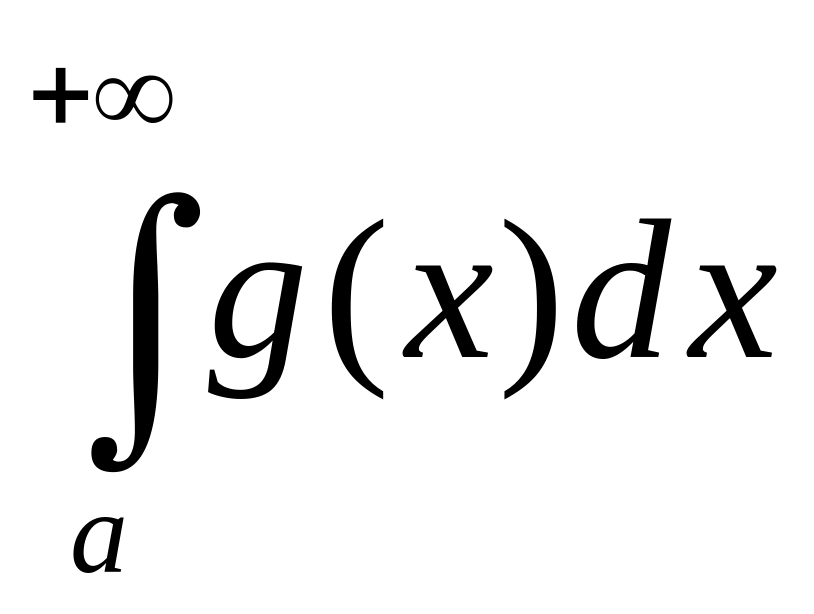сходится,
то
также сходится.
Следствие. (достаточное условие расходимости) Если и расходится, то также расходится.
Теорема 2
(предельный признак сравнения). Пусть
функция
а
и пусть
.
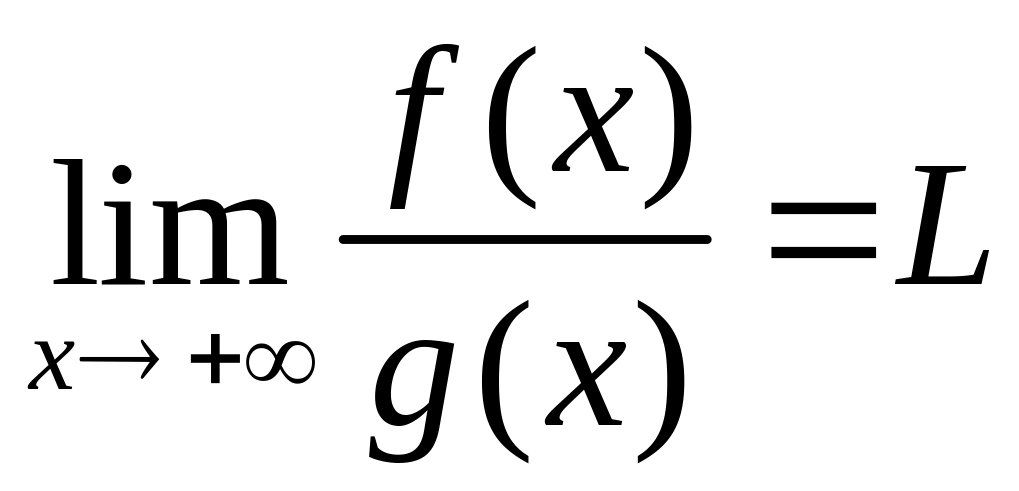Тогда:
1) если
сходится и
,
то
– также сходится;
2) если
расходится и
,
то
– расходится.
Следствие 1.
Если
и
, то
и
сходятся или расходятся одновременно.
Следствие 2.
Если
, то
сходится при
и расходится при
.
def.
Если интеграл
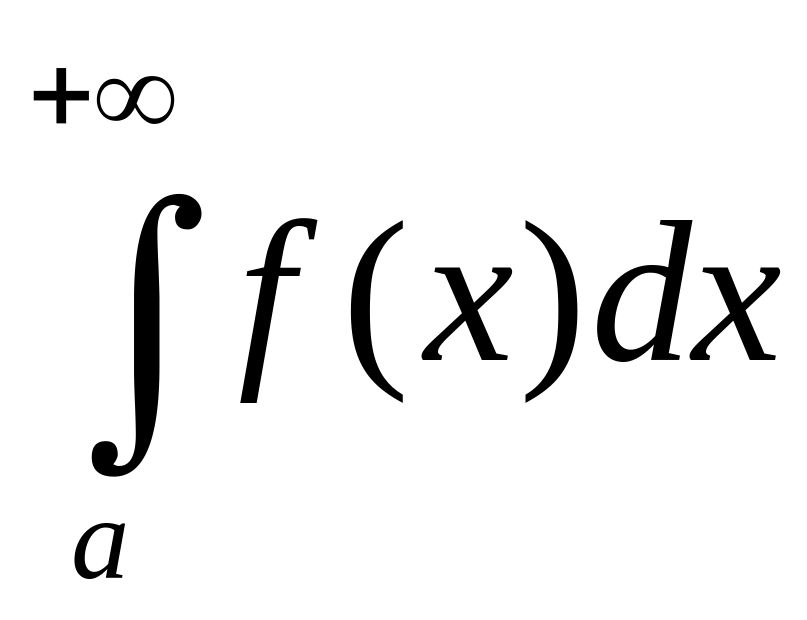сходится, а
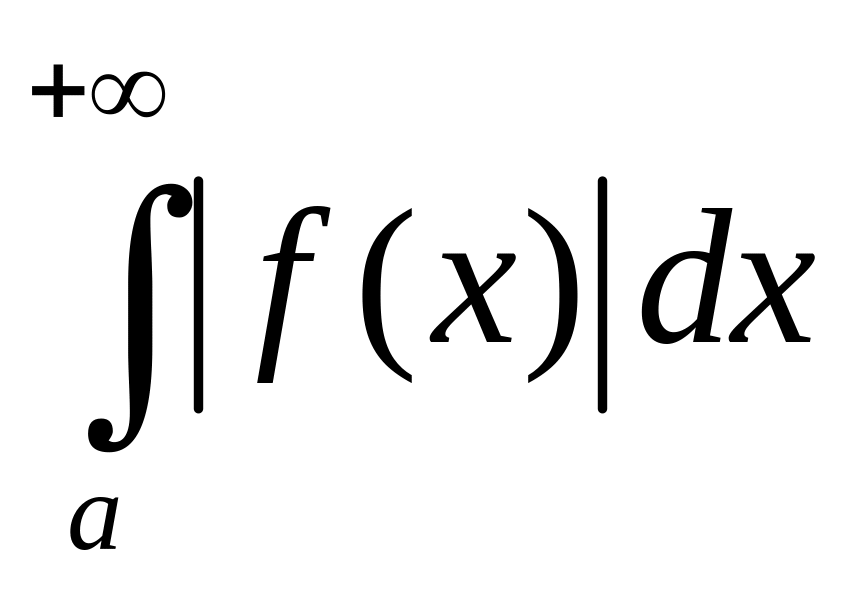– расходится, то интеграл
называется условно
(или
неабсолютно)
сходящимся.
Теорема 3
(Признак
Дирихле).
Пусть
функция
непрерывна
и имеет ограниченную первообразную
на
.
Пусть функция
является непрерывно дифференцируемой
и манатонной на
и
.
Тогда интеграл
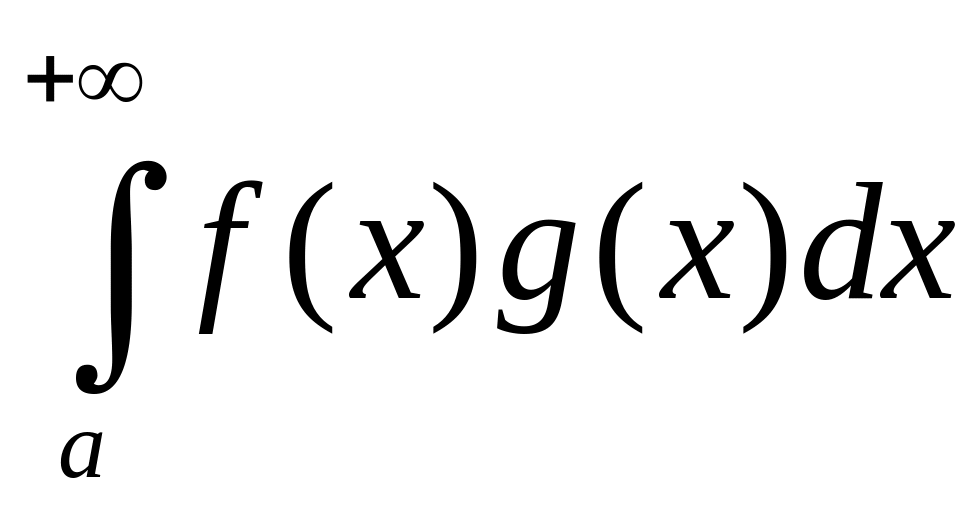– сходится.
def.
Если функция
неограничена в точке
,
и интегрируема на каждом отрезке
(в частности
является ограниченной на отрезке
), то точку
называют особой
точкой
функции
.
def.
Предел
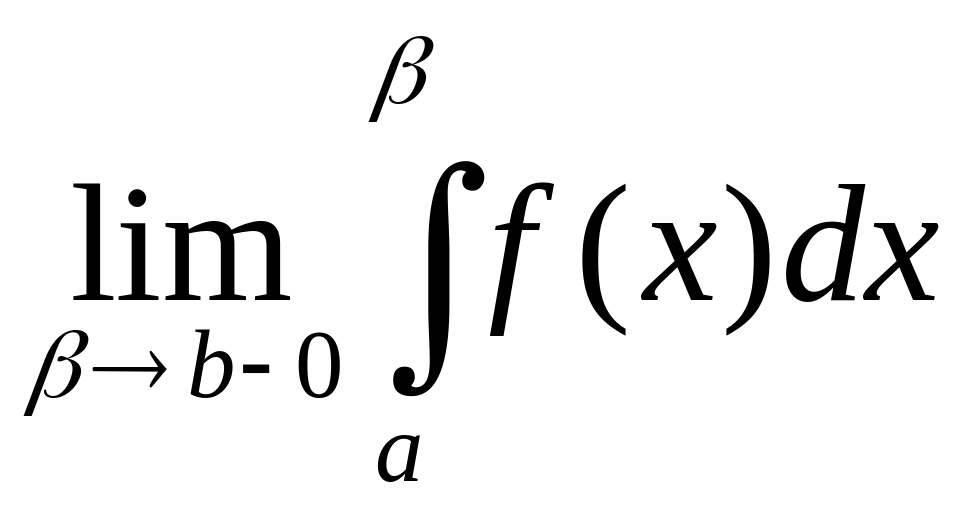называют несобственным
интегралом от неограниченной функции
на отрезке
(или несобственным
интегралом второго рода,
НИ-2) и обозначают
.
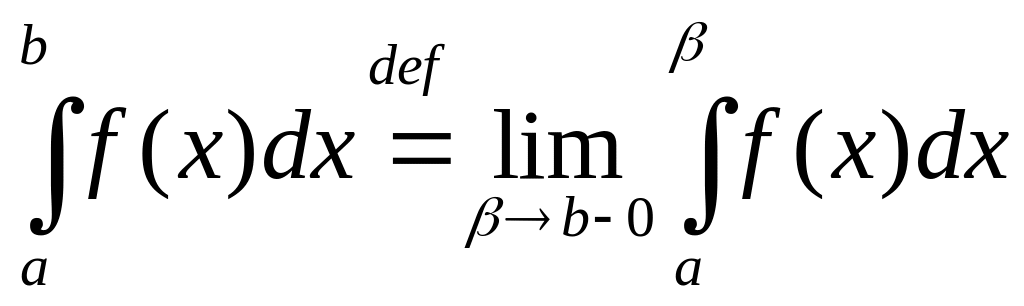Теорема 4
Если
,
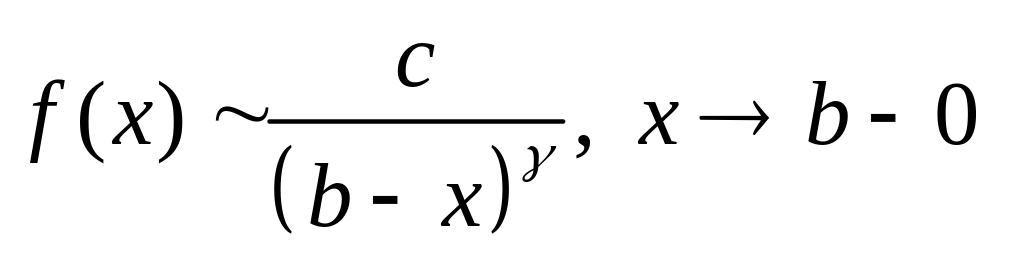то
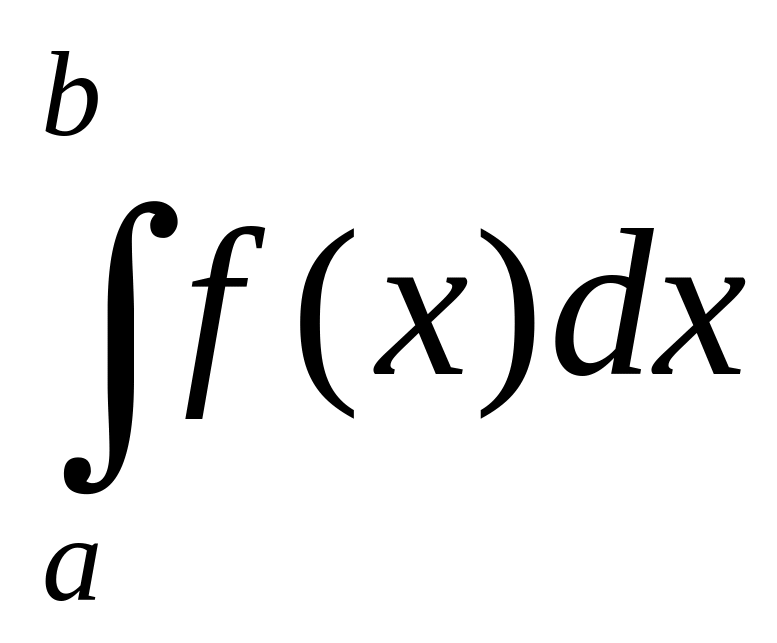сходится
только при
.
Задачи
1.1.
Вычислить интеграл
.
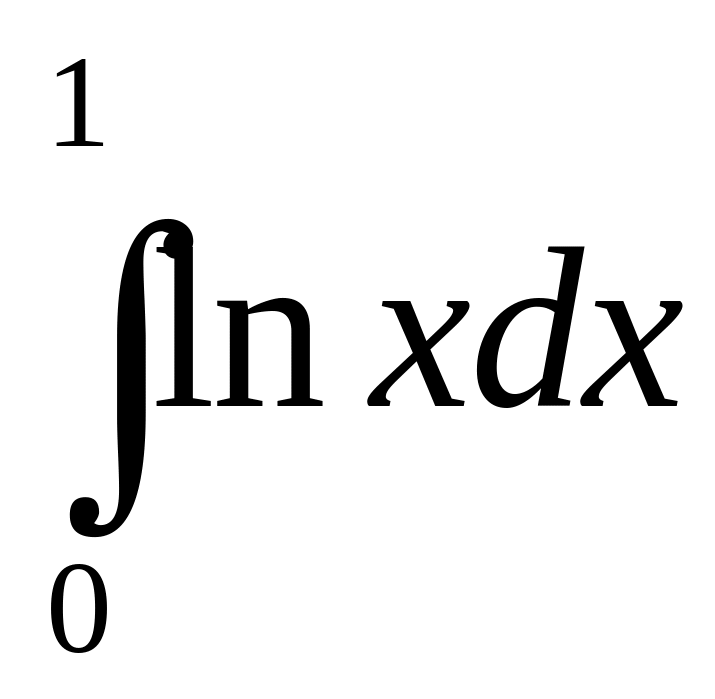1.2.
Исследовать на сходимость интегралы:
1)
;
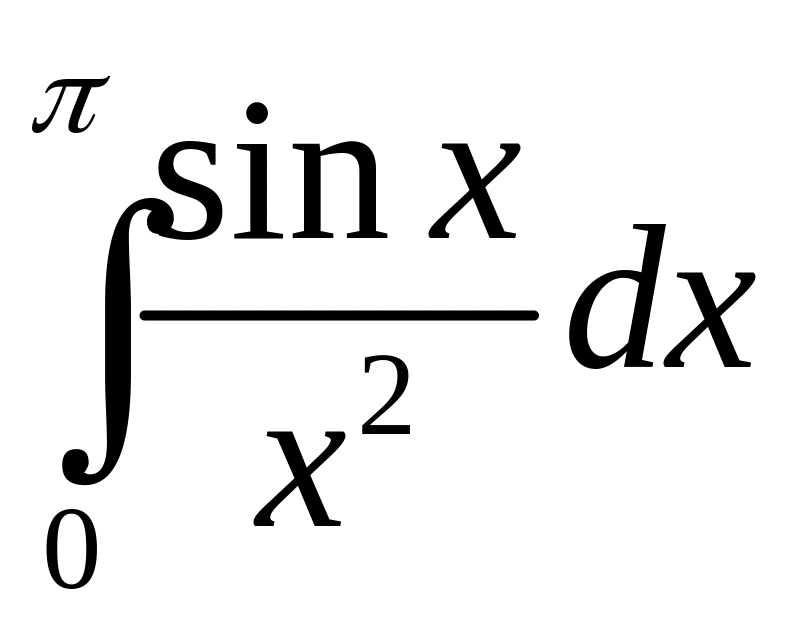2)
.
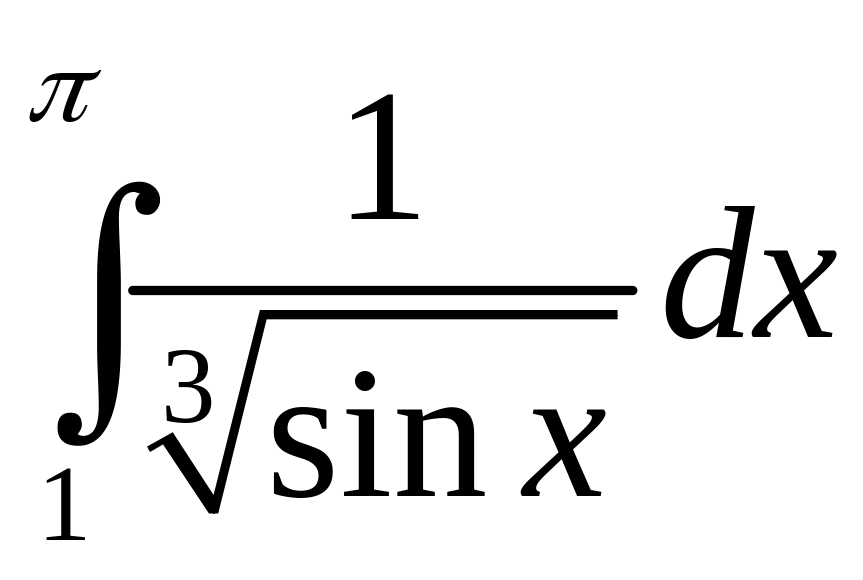1.3.
Исследовать на сходимость интегралы:
1)
;
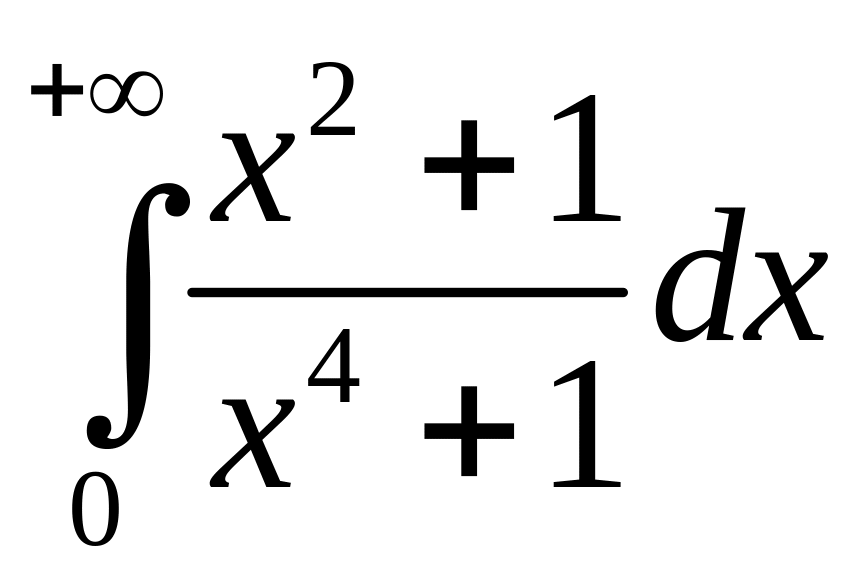2)
.
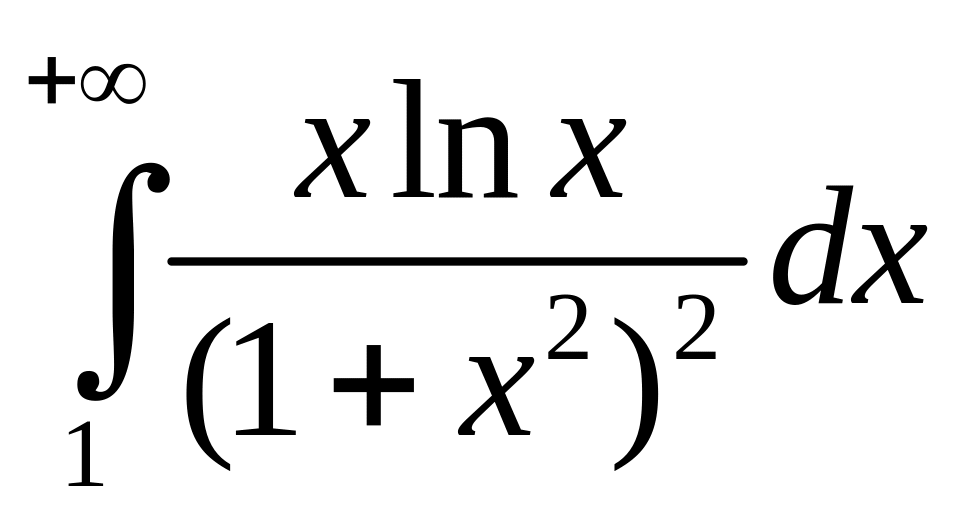1.4. Исследовать на сходимость интегралы:
1)
;
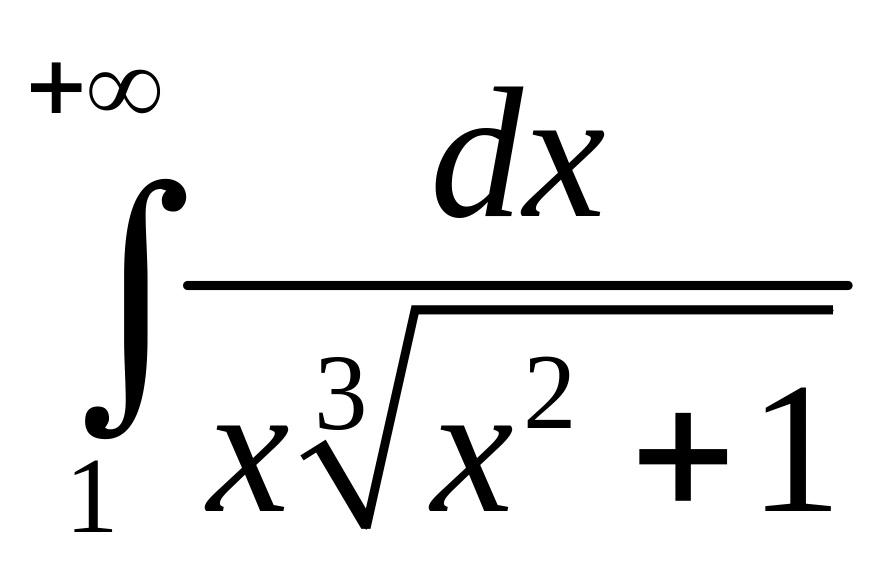2)
;
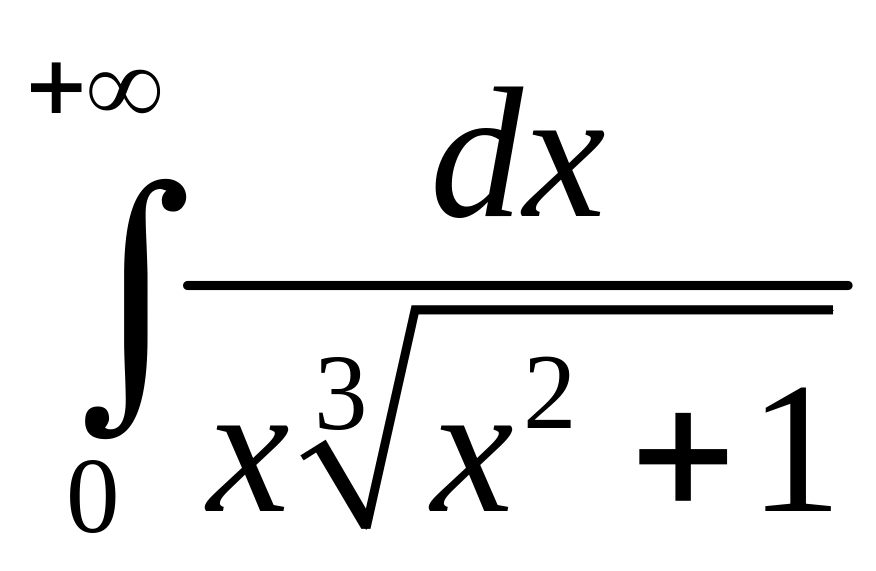3)
.
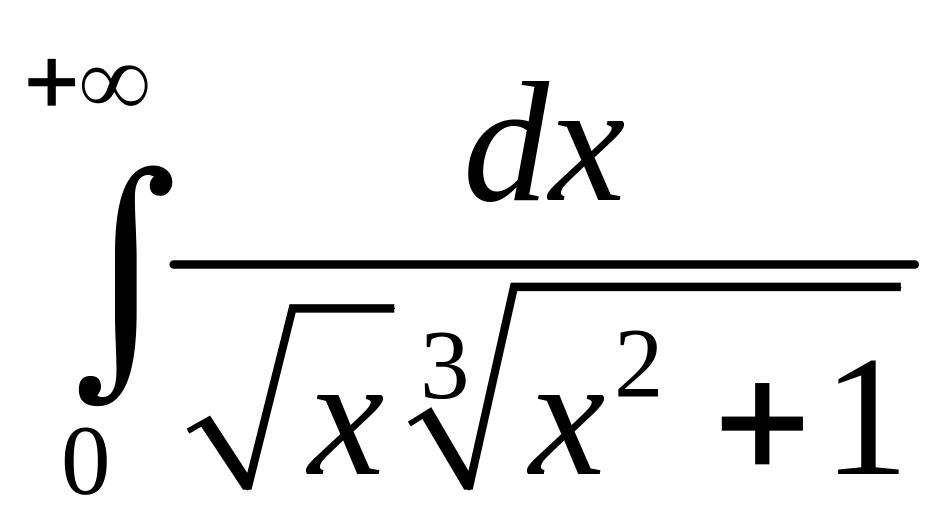1.5.
Исследовать на сходимость интегралы в
зависимости от параметров:
1)
;
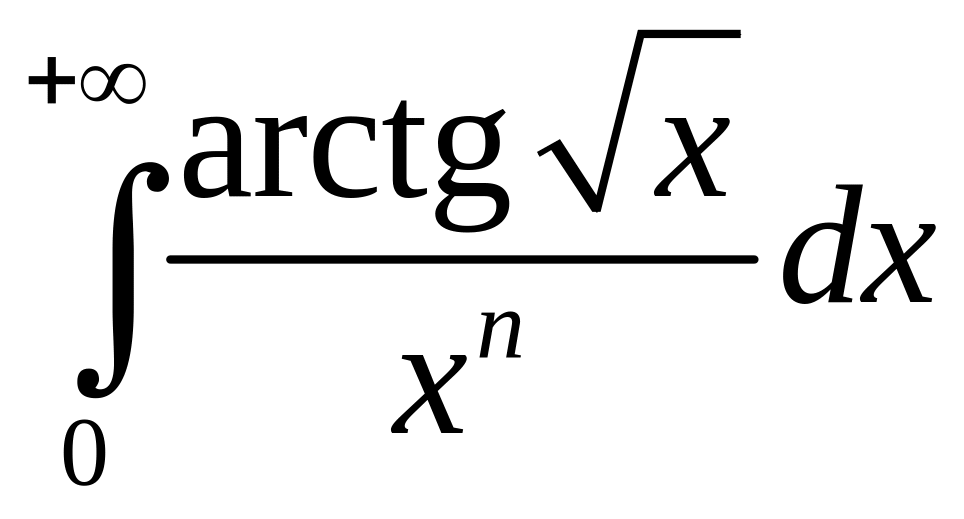2)
.
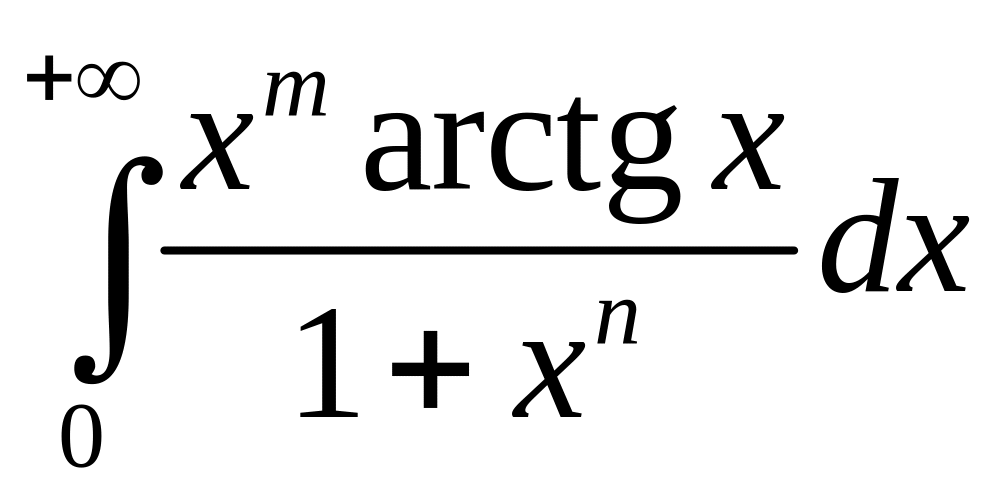1.6.
Исследовать на сходимость интегралы в
зависимости от параметров:
1)
;
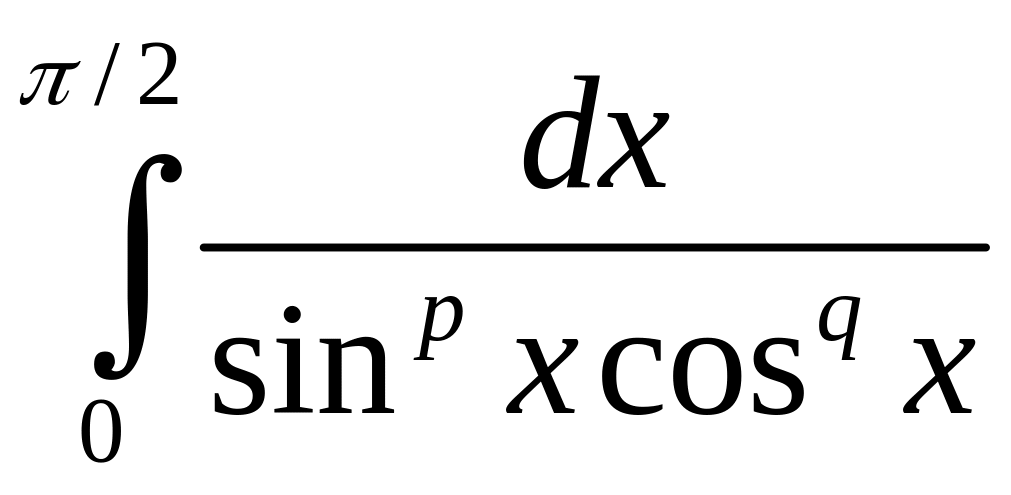2)
;
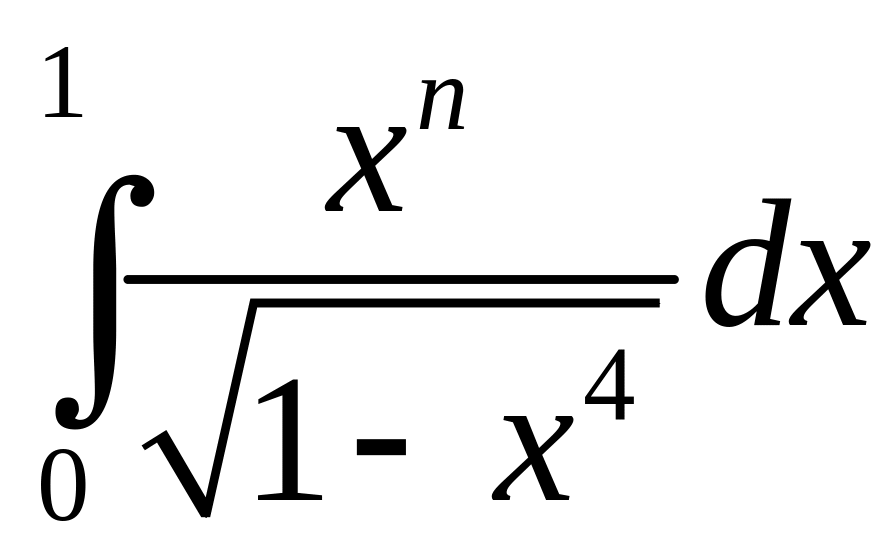3)
.
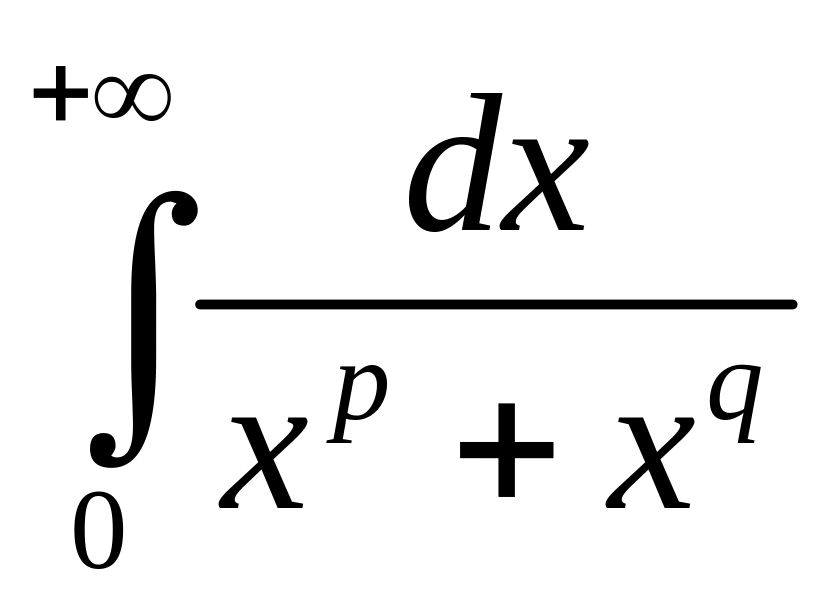1.7. Исследовать на абсолютную и условную сходимость:
1)
;
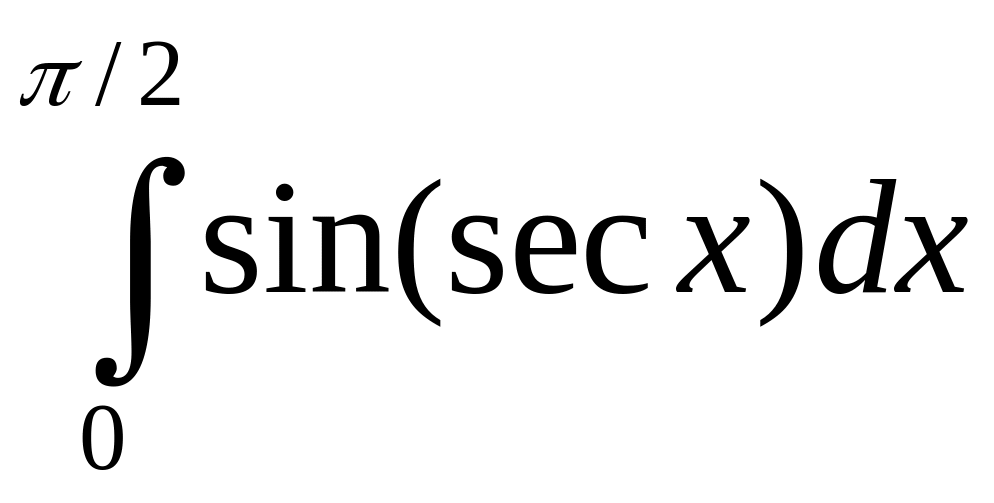2)
.
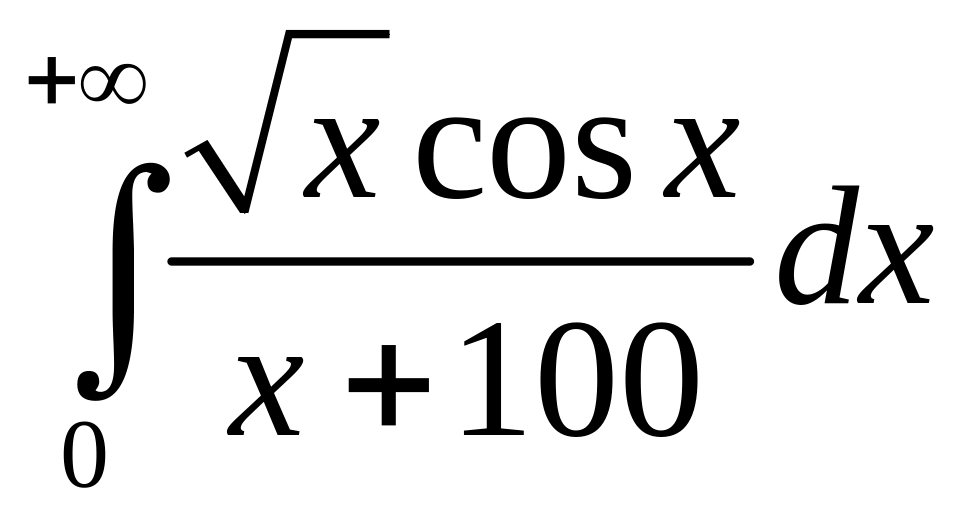Домашнее задание 1.
Исследовать на сходимость:
1.8.
.
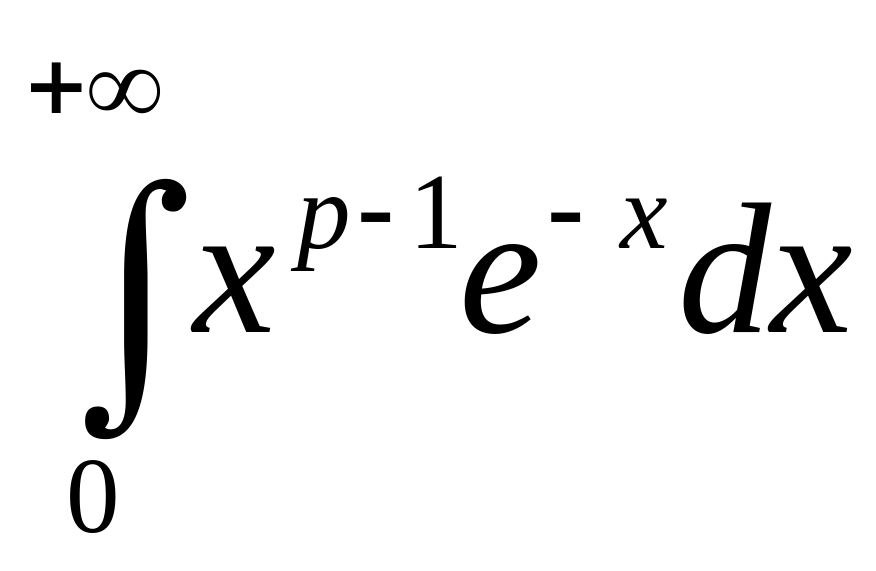1.9.
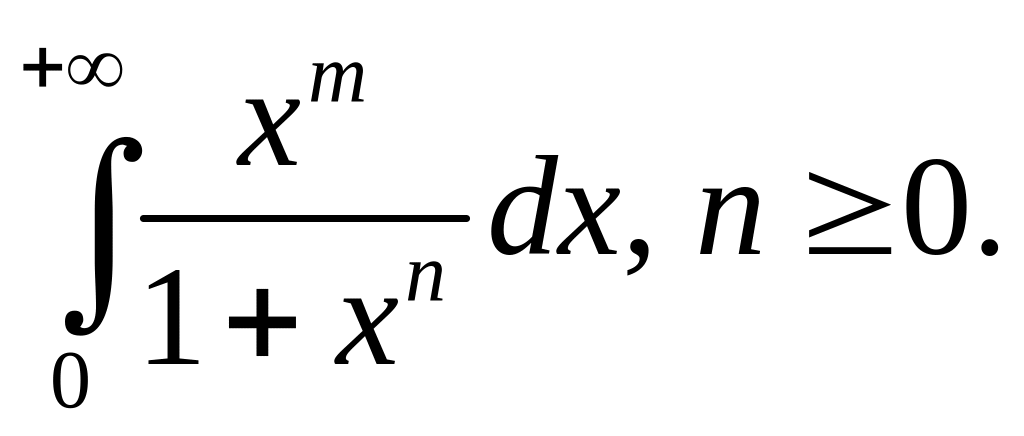1.10.
.
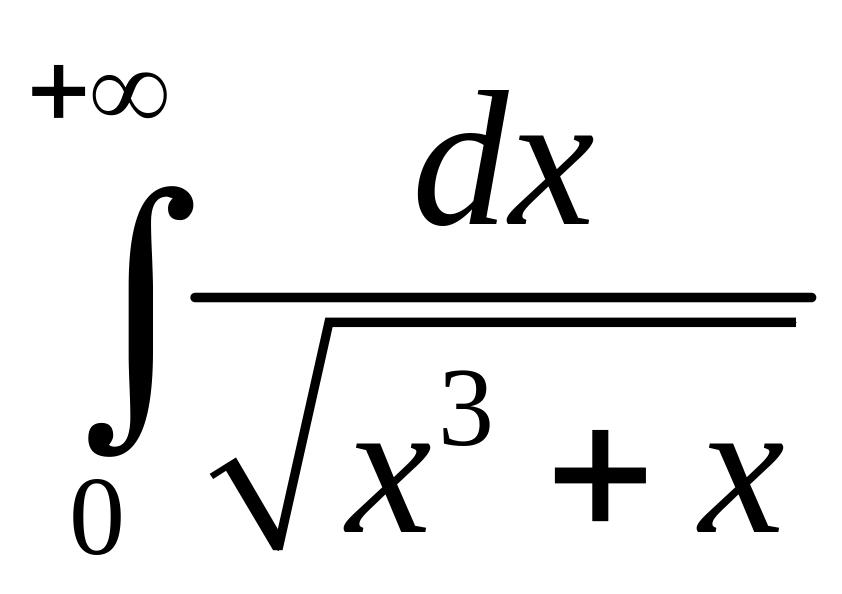1.11.
.
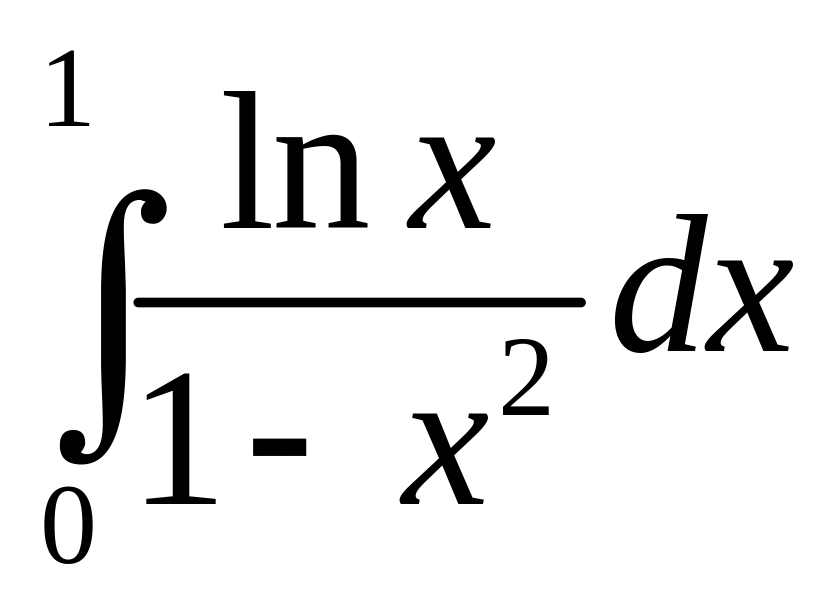1.12.
.
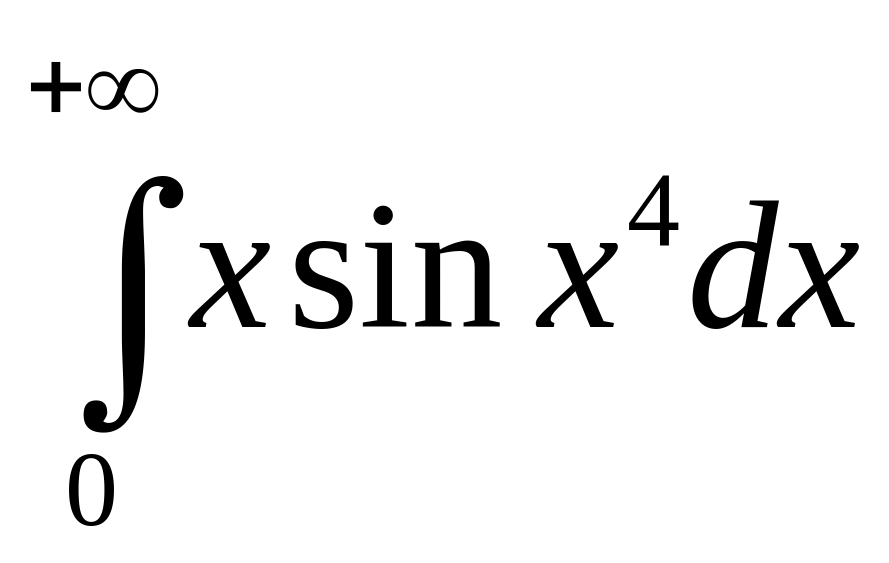Тема 2. Формула Тейлора: разложение.
Пусть функция
в некоторой окрестности точки
имеет производные до
-го
порядка включительно. Многочлен
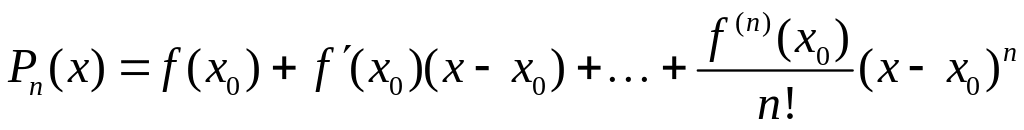
называется многочленом Тейлора
порядка
для функции
в точке
.
Обозначив
отклонение значений функции
от значений построенного для неё
многочлена Тейлора 
,
получаем
формулу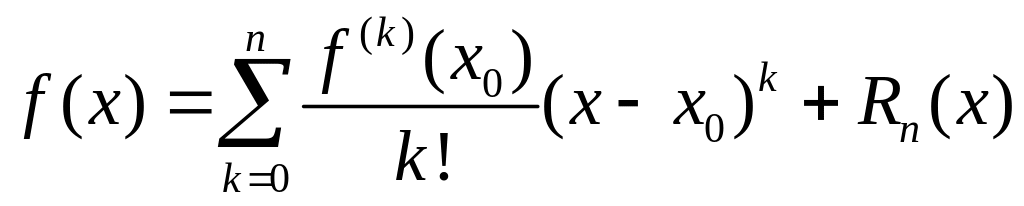 
,
которую называют формулой Тейлора
для функции
с
центром в точке
,
а
–
-м
остаточным членом формулы Тейлора.
В частном случае при
формулу Тейлора называют формулой
Маклорена.
При этом остаточный член формулы Тейлора
может быть представлен в виде
,
и его называют остаточным членом
в форме Пеано.
Замечание. Формула Маклорена для нечётной функции имеет вид:
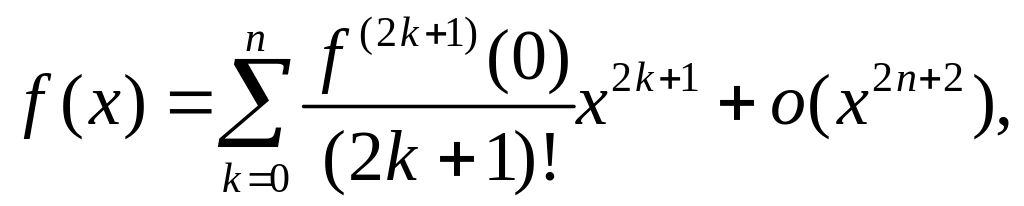
а для чётной функции:
.
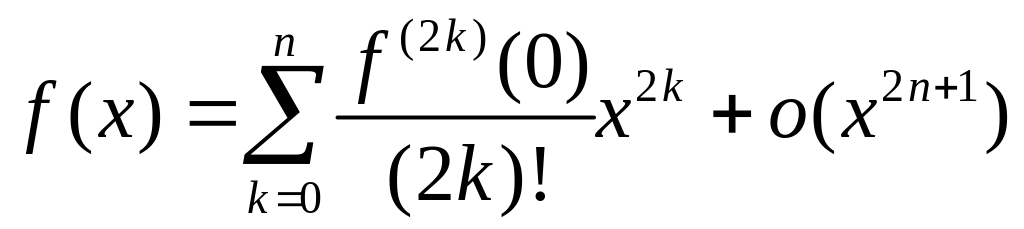