Коефіцієнтів

Загальне поняття демографічних коефіцієнтів. Середнє населення. Загальні та спеціальні коефіцієнти природного руху населення. Стандартизація демографічних коефіцієнтів

Поняття демографічних коефіцієнтів

_Населення – це сукупність людей, а демографічні процеси – це сукупність фактів (подій), що відносяться до окремих людей. Тому число подій залежить від загальної чисельності того середовища, де вони відбуваються, у нашому випадку – від чисельності населення.

Наприклад, число народжених дітей у 2006 р. становило: в Україні – 460 тисячі, в Росії – 1150, в Білорусі – 85 тисяч. Зрозуміло, що значення цих подій не можуть бути співставленні, бо вони відбулися в різних сукупностях – відповідно – 46,9 млн. осіб, 142,8 і 9,8 млн. осіб.

Абсолютні числа демографічних подій, як і абсолютна чисельність населення, не можуть прямо використовуватися ні для характеристики демографічних процесів, ні для міжтериторіальних або динамічних порівнянь, ні для оцінки структурних характеристик населення.

Тому для оцінки інтенсивності демографічних процесів та їх порівняння за територіями та у динаміці недостатньо знати лише їх абсолютне значення. Величину демографічних процесів необхідно співвіднести з чисельністю населення, в якому вони відбувалися.

Це приводить до необхідності застосування в демографічному аналізі відносних величин, розрахованих як відношення числа подій до чи­сельності населення. Такі величини називаються демографічними коефіцієнтами.

Демографічні коефіцієнти – це відносні величини, що характеризують інтенсивність демографічних процесів в цілому населенні, або в певній його частині. Під інтенсивністю слід розуміти кількість подій в одиницю часу (рік, місяць, день). При розрахунку демографічних коефіцієнтів виникає проблема порівняння числа подій та чисельності населення. Як вже відомо, дані про чисельність населення фіксуються станом на певний момент часу (на 1 січня або іншу дату) і представляють собою мо­ментні показники. А демографічні процеси (народження, смерті, шлюби, розлучення, переміщення населення) відносяться до певного періоду часу, які можуть бути різними. (в демографії, як правило, розрахунки проводять за періоди, що дорівнює 1 року). Такі показники називаються інтервальними або періодичними.

Середнє населення

Проблему порівняння моментних та інтервальних показників можна вирішити двома шляхами. Перший – це перетворити інтервальні показники в моментні за допомогою скорочення довжини інтервалу часу, для якого фіксується демографічна подія. Якщо припустити, що цей інтервал перетворюється в "0", то ми одержимо показник, який називається силою демографічного процесу ²².

Другим шляхом є перетворення моментного показника в інтервальний. Цього можна досягнути методом усереднення чисельності населення, тобто розрахунку показника, який характеризував би населення не на якийсь момент, а за період у цілому. Цим показником виступає число людино-років, прожитих населенням за певний період, або його приблизне значення – середнє населення.

Середнє населення – узагальнюючій показник чисельності населення за період, що виступає однією з оцінок числа людино-років, прожитих населенням протягом даного періоду.

Якщо розглядати населення як функцію часу S(t), то розрахунок середнього населення буде представлено таким чином:

S_x

S₂

S (t)

S₁

t₂

t₁

де: S₁ і S₂ – чисельність населення на початок і кінець періоду; t₁ і t₂ – моменти початку і кінця періоду; (t₂ – t₁₎ – тривалість періоду.

Площа фігури S₁S₂t₂t_1. дорівнює числу людино-років, прожитих населенням у період от t₁ до t₂, тобто:

(4.1)

Розділивши його на тривалість періоду, одержимо середнє населення:

(4.2)

Одиницею часу в демографії, як правило, є рік, тобто t₂ – t₁ = 1. В такому разі ділення на 1 відпадає, і середня чисельність населення можна обчислити за формулою: Із наведених розрахунків видно, що середнє населення – це число людино-років, прожитих сукупністю людей за певний період часу.

Число людино-років, прожитих населенням за певний період, дозволяє найбільш точно врахувати той очевидний факт, що різні люди в межах одного й того ж періоду проживають різну його частку. Кожна людина конкретного населення може прожити в ньому або весь період, або якусь його частину. Цим визначається індивідуальний вклад, який вносить людина в загальну чисельність населення. Це можна проілюструвати на прикладі таких умовних даних (табл. 4.1):

Таблиця 4.1

Розрахунок числа людино-років, прожитих населенням

Події і дати	Кількість людей	Число прожитих днів	Число прожитих людино-років
Населення на 1 січня	1000	х	х
Проживало постійно на протязі року	850	310250	850
Народилося 1.02	5	1670	4,58
Народилося 1.07	5	920	2,52
Приїздили в місто в середньому на 20 днів	50	1000	2,74
Приїхали для постійного проживання 1.10	20	1840	5,04
Померло 1.09	8	1944	5,33
Виїздили з міста у відпуску у середньому на 24 дні	56	1344	3,68
Виїхали на постійне проживання в інші міста 1.08	22	4664	12,78
Усього прожито людино-років	х	х	879,3
Населення на 31 грудня	1000	х	х

Для розрахунку загального числа людино-років, прожитих населенням у даному населеному пункті протягом року, необхідно просумувати час, протягом якого кожна людина знаходилася у складі даної сукупності.

Такі розрахунки можливі лише для невеликих населених пунктів і за умов чітко поставленого обліку природного руху населення та міграції.

Практично ми не можемо знати значення S(t) – тобто точну чисельність населення на будь-який момент часу, тому що статистичний облік населення дозволяє одержувати це значення тільки на певну дату, як правило, на початок року.

Тому на практиці обмежуються розрахунком показника, який є наближеним значенням загального числа людино-років і називається "середнім населенням". Одним з таких показників є населення на середину періоду.

При розрахунках середнього населення користуються математичною моделлю зміни чисельності населення протягом року. Вважають, що населення змінюється або рівномірно (лінійно, в арифметичній прогресії), або с постійним темпом (експоненціально, в геометричній прогресії).

Якщо виходити з гіпотези, що протягом періоду населення змінюється рівномірно, тобто у арифметичній прогресії, то середнє населення представляє собою полусуму чисельності населення на початок і кінець року:

або тотожна їй формула: (4.3)

де: S₀ і S₁ – чисельність населення відповідно на початок і кінець періоду.

Для більш тривалішого періоду від цієї формули доводиться відмовлятися тому, що вона не враховує коливання чисельності населення, які відбуваються протягом періоду. і використовувати інші методи.

Якщо відомі дані не тільки на початок і кінець періоду, а й на проміжні дати, середню чисельність можна розрахувати за формулою середньої хронологічної моментного ряду (при рівній довжині періодів між датами, на які є дані про чисельність населення):

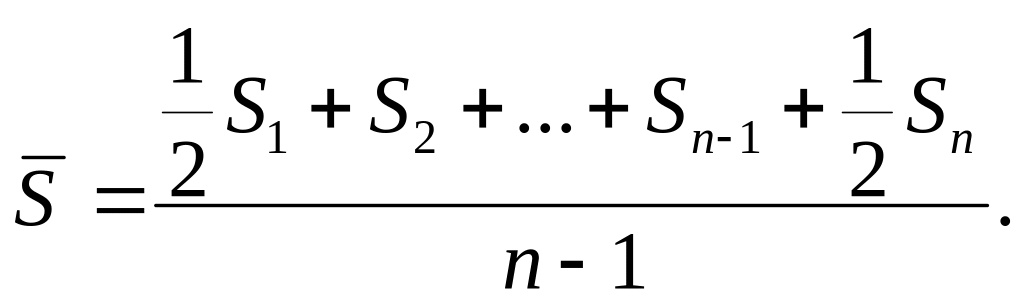(4.4)

де: S₁, S₂ …S_n – чисельність населення на початок відповідного періоду; n – число дат; n – 1 – число періодів.

Якщо тривалість періодів не рівні між собою, то розрахунок середньої чисельності населення проводиться за формулою середньої арифметичної зваженої:

(4.5)

де: – середнє населення i – го періоду; t_і – довжина i – го періоду; .

Для періоду тривалістю 10 – 15 і більше років використовують гіпотезу зміни чисельності населення з постійним темпом (у геометричній прогресії). Тоді середнє населення обчислюється з використанням формули безперервного темпу приросту:

(4.6)

де: S₀ і S₁ – чисельність населення відповідно на початок і кінець періоду; е – основа натуральних логарифмів; k – середній темп приросту населення; t – період часу.

Звідки витікає, що:

(4.7)

де: 1/Т – половина тривалості періоду Т, за який розраховується середнє населення.

Якщо проінтегрирувати в інтервалі від 0 до t, знайдемо:

(4.8)

тобто середнє населення представляє собою відношення приросту чисельності населення до приросту його натуральних логарифмів.

Проведемо розрахунок за даними таблиці 3.1 про чисельність населення України у 2000-2006 рр.

Середнє населення за формулою (4.3) середньої простої складатиме:

за формулою (4.4) середньої хронологічної:

за формулою (4.8) безперервного темпу приросту:

Як видно, розрахунки за різними формулами дали різні результати, що пояснюється різними гіпотезами щодо розвитку населення.