Лабораторная работа № 121

«Определение температурной зависимости электропроводимости металлов и полупроводников»

Цель работы – углубление представлений о физических свойствах твердых тел.

Приборы и оборудование: нагреватель с масляной ванной, металлическое и полупроводниковое сопротивление, термометр, магазин сопротивлений, реохорд, гальванометр.

Общие сведения Электропроводимость может быть выражена следующими формул:

для полупроводников

σ = q·n·u , (1)

где q – электрический заряд носителей, создающих электрический ток;

п – концентрация носителей заряда;

– подвижность носителей заряда, равная отношению средней скорости <υ_уп> упорядоченного движения носителей к напряженности Е электрического поля, вызвавшего это движение;

для металлов

, (1а)

где – средняя длина свободного пробега электрона, имеющего энергию Ферми,

– средняя скорость теплового движения такого электрона.

В зависимости от электропроводимости, все твердые тела делятся на три группы: проводники, непроводники (диэлектрики) и полупроводники. Каждой из этих групп присуща своя энергетическая схема, обусловленная особенностями расщепления энергетических уровней электронов в зоны при объединении атомов в кристалл. В энергетической схеме обычно выделяют валентную зону (ВЗ) и зону проводимости (3П).

Валентной зоной называется зона, образовавшаяся от расщепления того уровня, на котором в уединенном атоме находятся валентные электроны. Выше этой зоны в энергетической схеме невозбужденного атома располагаются не занятые электронами зоны.

Зоной проводимости называется низшая по энергии, не полностью заселенная электронами разрешенная зона. Электроны этой зоны обеспечивают создание электронной составляющей проводимости.

Энергетическая схема проводников (рис. 1), к которым относятся металлы, имеет не полностью заселенную валентную зону.

Рис. 1

Эта зона является здесь зоной проводимости. Разница в энергиях соседних уровней схемы очень невелика (≈10^-22 – 10^-23 ) эВ, поэтому переход электронов на более высокие энергетические уровни требует незначительной энергии внешнего поля. Это обстоятельство в сочетании с высокой концентрацией свободных электронов порядка 10²⁸ – 10²⁹ м^-3 обусловливают хорошую электропроводимость металлов.

Концентрация носителей заряда (свободных электронов) в чистых металлах почти не зависит от температуры.

Квантовая теория рассматривает движение электронов в металле с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде – она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току – упорядоченному движению электронов – никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния (порядка сотен периодов решетки).

В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами (фононы есть кванты энергии звуковых (упругих) волн; являются квазичастицами – элементарными возбуждениями, ведущими себя подобно микрочастицам; описывают упругие колебания кристаллической решетки; фононы сильно отличаются от обычных частиц – электронов, протонов, фотонов, – т.к. они связаны с коллективным движением многих частиц системы; существуют только в кристалле).

Согласно классической теории, ~ , поэтому она не смогла объяснить истинную зависимость электропроводности от температуры. В квантовой теории средняя скорость от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышенном температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур средний свободный пробег электрона ~ Т ^-1, поэтому, учитывая независимость от температуры, получим, что сопротивление металлов (R ~ 1/σ)в соответствии с данными опытов растет пропорционально T (см. формулу 1а).

Степень влияния температуры на электропроводимость металлов различна для разных температур. На графике зависимости σ (Т) для несверхпроводников (рис.2) можно выделить три участка:

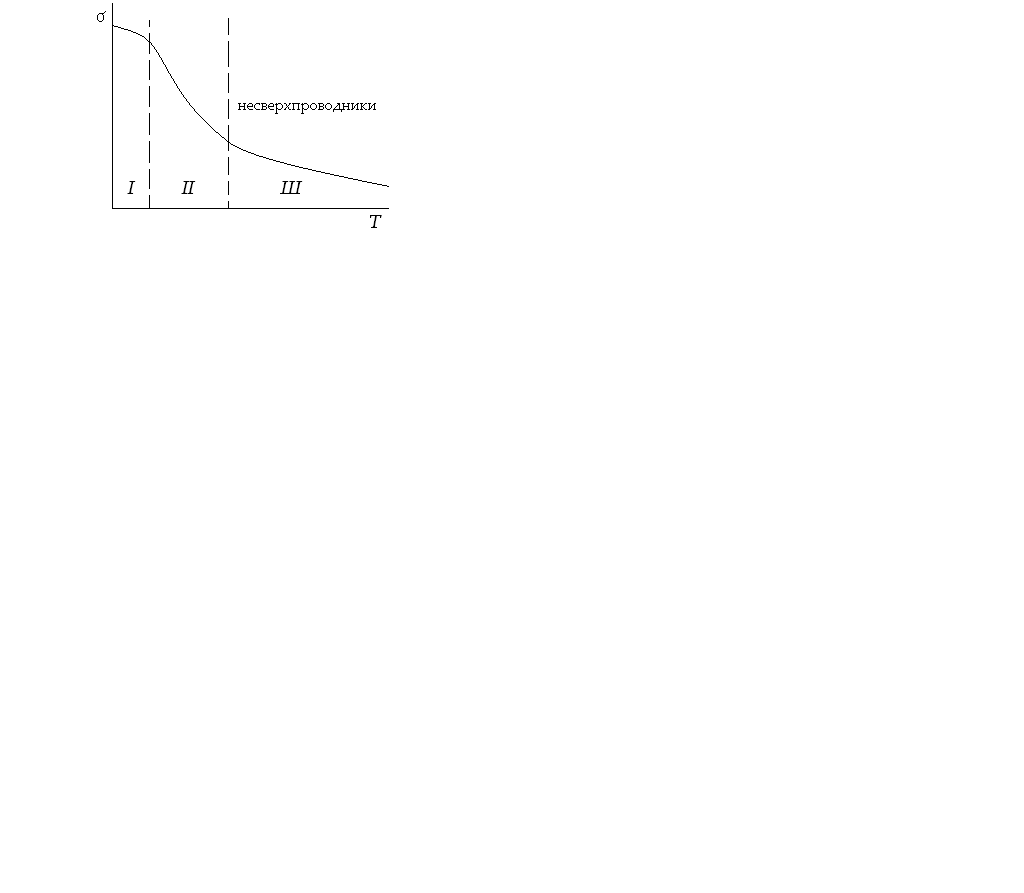
Рис. 2

III – участок нормальных и высоких температур, на котором электропроводимость обратно пропорциональна температуре, т.е. σ ~ Т ^-1;

II – участок низких температур, для которого справедлива приближенная зависимость σ ~ Т ^-3;

I – участок очень низких температур, близких к 0 К, на котором электропроводимость почти не зависит от температуры (она называется остаточной).

Неизменность электропроводимости металлов в области очень низких температур объясняется следующим. При этих температурах тепловые колебания решетки становятся незначительными, и основное влияние на движение носителей оказывает не взаимодействие с узлами решетки кристалла, а взаимодействие с атомами примеси и вакансиями. Интенсивность же этого взаимодействия почти не меняется с температурой, что обусловливает неизменность подвижности носителей и электропроводимости вещества.

Для практики наибольший интерес представляет область нормальных и повышенных температур (участок III), где σ ~ 1/Т. При этом чаще всего рассматривают температурную зависимость удельного сопротивления вещества ρ=1/σ, или абсолютного сопротивления R:

или (2) Здесь: ρ₀ , R₀ – сопротивление образца при T_C = 0ºC;

Т_C – температура по шкале Цельсия;

α – температурный коэффициент сопротивления;

;

l – линейный размер проводника;

S - площадь его поперечного сечения.

Полупроводниками называют вещества, электропроводимость которых при температуре 0 К равна нулю и становится больше нуля лишь под влиянием внешних факторов, например, тепловых воздействий,

Для полупроводников различают собственную электропроводимость, имеющую место в химически чистом веществе, и примесную проводимость, обусловленную введением в вещество атомов примеси.

Возникновение собственной электропроводимости в полупроводнике объясняется так. Под воздействием тепла происходит отрыв от атомов кристалла электронов парноэлектронных (ковалентных) связей, которые слабее других связаны с ядрами атомов (рис. За). Оторвавшиеся электроны становятся свободными и под влиянием внешнего электрического поля упорядоченно перемещаются по всему кристаллу. Этим создается электронная составляющая проводимости. Отрыв электрона от атома приводит к появлению в этом месте избыточного положительного заряда – так называемой дырки. Дырка может захватить электрон соседнего атома и исчезнуть, но тогда избыток положительного заряда возникнет в другом атоме. При действии внешнего электрического поля процесс перемещения дырок идет упорядоченно в направлении напряженности поля. Этим создается дырочная составляющая проводимости.

Рис. 3

Энергетическая схема собственного полупроводника представлена на рис. 3б. Здесь при Т = 0 К валентная зона заселена электронами полностью. Она отделена от следующей разрешенной пустой при Т = 0 К зоны неширокой запрещенной зоной ΔЕ₃. Для типичных полупроводников – германия и кремния – ΔЕ₃ составляет 0,66 эВ и 1,1 эВ. Отрыв электрона от атома отображается на схеме в виде перехода его из валентной зоны в следующую пустую разрешенную зону. Движение электронов зоны проводимости представляет электронную составляющую проводимости, а переходы электронов на освободившиеся дырки в валентной зоне – ее дырочную составляющую.

Таким образом, для полупроводников характерны два типа проводимости: электронная и дырочная. При этом направления движения электрона и дырки под действием внешнего поля противоположны, поэтому общую проводимость полупроводника можно выразить так:

. (3)

Здесь индекс «n» относится к электронной составляющей, а индекс «p» – к дырочной составляющей электропроводимости.

Заменив величины п и и, можно привести формулу (3) электропроводимости собственного полупроводника к виду

, (4)

где σ_0с – величина, которую в первом приближении можно считать константой; она определяется главным образом природой вещества;

k – постоянная Больцмана;

ΔЕ_З – энергия запрещенной зоны (энергия активации).

Введение примеси способствует увеличению проводимости полупроводника. Различают донорные примеси, валентность атомов которых больше валентности атомов основного вещества. и акцепторные примеси, валентность атомов которых меньше валентности атомов основного вещества.

В отличие от собственной проводимости, примесная проводимость является однотипной – или электронной, или дырочной.

Электронная примесная проводимость возникает при внедрении донорной примеси за счет отрыва от атомов примеси валентных электронов, не участвующих в создании парноэлектронных связей. Это имеет место, например, при внедрении атомов пятивалентного мышьяка в кристалл четырехвалентного германия. Здесь в создании связей заняты только четыре валентных электрона мышьяка, а пятый легко отрывается от ядра и становится свободным. На энергетической схеме такого полупроводника (рис. 4а) отрыв электрона отображается его переходом с донорного уровня Е_Д в зону проводимости (ЗП).

Поскольку донорные уровни Е_Д располагаются вблизи дна зоны проводимости Е_с, то для такого перехода необходима меньшая энергия, чем для перехода электрона из валентной зоны в зону проводимости. Это способствует увеличению концентрации свободных электронов и повышению проводимости.

Дырочная проводимость возникает при внедрении акцепторной примеси, например, трехвалентного индия в четырехвалентный германий. В этом случае число валентных электронов атомов примеси оказывается недостаточным для создания полного комплекта его связей с соседними атомами основного вещества. Недостающий электрон захватывается у одного из атомов основного вещества и на его месте образуется дырка. Перемещаясь по кристаллу, дырка обеспечивает перенос заряда. На энергетической схеме дырочного полупроводника (рис. 46) образование дырки отображается переходом электрона из валентной зоны на акцепторный уровень Е_АК. Поскольку акцепторные уровни расположены вблизи потолка валентной зоны Е_V, то для такого перехода электрона требуется меньшая энергия, чем для перехода из валентной зоны в зону проводимости. Это обеспечивает повышение электропроводимости вещества.

Формулы электропроводимости примесных полупроводников можно представить в виде:

,

(5)

,

Рис. 4

где Е_Д, Е_АК – энергия донорных уровней, отсчитанная от дна зоны проводимости Е_С, и акцепторных уровней, отсчитанная от потолка валентной зоны Е_V;

σ_0n, σ_0p – величины, в первом приближении постоянные.

Повышение температуры приводит к возрастанию электропроводимости полупроводников, причем определяющим фактором, вызывающим изменение электропроводимости, является изменение концентрации носителей заряда.

Приближенно концентрацию носителей заряда в полупроводнике можно выразить так:

, (6)

где E – энергия, необходимая для возникновения свободного носителя заряда, а с_n – коэффициент , слабо зависящий от температуры.

Формула (6) показывает, что главное влияние на изменение концентрации носителей с температурой оказывает множитель . Множитель же Т^3/2 – меняется не столь существенно. Общее влияние температуры на величину п и электропроводимость полупроводника σ очень велико: например, при повышении температуры от 100К до 600К электропроводимость полупроводника возрастает на 17 порядков.

Подвижность носителей заряда в полупроводнике, как и в металле, с увеличением температуры снижается, но влияние этого фактора не является определяющим.

Логарифмическая зависимость электропроводимости от величины 1/T представлена на рис.5. Здесь можно выделить три участка:

I – участок, соответствующий интервалу температур, на котором главную роль играет собственная проводимость;

II – промежуточный участок истощения примеси;

III – участок, соответствующий интервалу температур, на котором определяющей является примесная проводимость.

На участках I и III основное влияние на электропроводимость полупроводника оказывает изменение концентрации, поэтому здесь с повышением температуры электропроводимость возрастает. Что касается участка II истощения

Р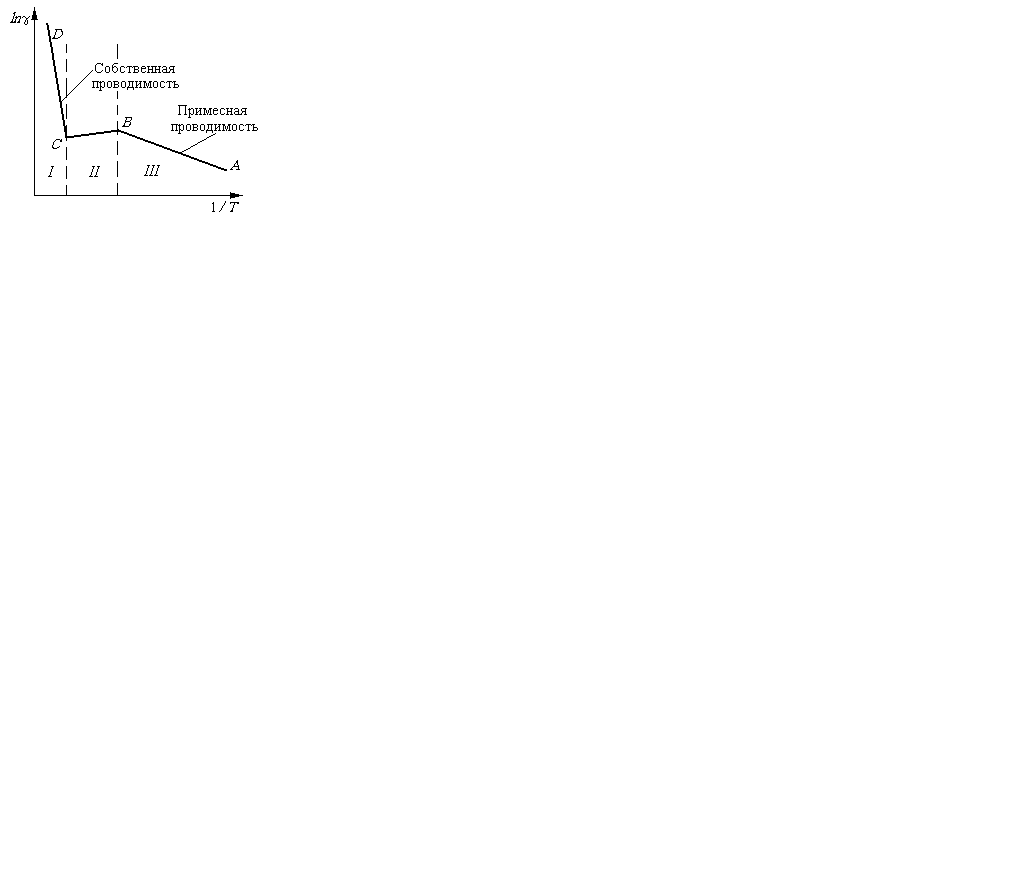 ис. 5

примеси, то при этих температурах все примесные носители уже задействованы, а интенсивной генерации собственных носителей еще не происходит. Поэтому здесь концентрация носителей почти не изменяется, а решающую роль играет изменение подвижности носителей. И если в полупроводнике основным является рассеяние энергии на тепловых колебаниях решетки, то проводимость на участке II будет уменьшаться. Используя зависимость , можно определить ширину запрещенной зоны ΔЕ_З, полупроводника и энергию активации примесных носителей.