МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Експериментальна перевірка залежності швидкості вібротранспортування від інтенсивності режиму методичні вказівки

до лабораторної роботи № 9

з дисципліни „Основи автоматики та автоматизації в галузі”

для студентів базового напрямку

6.0902 „Інженерна механіка”

Затверджено

на засіданні кафедри

"Автоматизація та комплексна

механізація машинобудівної промисловості"

Протокол № 4 від 25.10.2006 р.

ЛЬВІВ – 2007

Е кспериментальна перевірка залежності швидкості вібротранспортування від інтенсивності режиму. / Методичні вказівки до лабораторної роботи №9 з дисципліни „Основи автоматики та автоматизації в галузі”, для студентів базового напрямку 6.0902 „Інженерна механіка” / Укл. В.М.Боровець, О.Р. Серкіз, В.С. Шенбор, Я.В.Шпак– Львів, НУ “ЛП“, 2007.- 16 с.

Укладачі:

Боровець В.М., канд. тех. наук, доц., Серкіз О.Р., канд. тех. наук, доц., Шенбор В.С., ст. викладач., Шпак Я.В., канд. тех. наук, доц.

Відповідальний за випуск: Гаврильченко о.В канд.Техн.Наук., доц.

Рецензенти: Кусий Я.М. канд.техн.наук., доц.,

Савчин Б.М. канд.техн.наук., доц.

ВСТУП

Вібраційні завантажувальні і транспортні пристрої отримали широке розповсюдження як міжопераційний транспорт в автоматах, автоматичних лініях, роботизованих комплексах і гнучких автоматизованих виробництвах. Це обумовлено універсальністю, простотою керування і їх енергоощадністю.

1. Мета роботи

1. Ознайомлення з вихідними положеннями, гіпотезами і результатами теорії вібротранспортування для режимів з підкиданням, що встановилися під час прямолінійних гармонічних коливань лотка.

2. Вивчення конструкції і принципу роботи вібраційного лотка-транспортера.

3. Вивчення методу і набуття навиків встановлення заданої амплітуди на коливальному об'єкті за допомогою мікроскопа.

4. Експериментальне визначення коефіцієнта швидкості к_ш для різноманітних матеріалів і параметрів перевантаження W та побудова залежності , (залежність коефіцієнта швидкості від параметра перевантаження і параметра кута вібрації).

5. Порівняння експериментальних даних з розрахунковими.

2. Основні положення, гіпотези і результати теорії вібраційного транспортування для режимів з підкиданням, що встановилися при прямолінійних гармонічних коливаннях

Процес вібраційного транспортування більшості деталей прямолінійним нахиленим лотком, що здійснює гармонійні коливання за прямолінійною траєкторією, в теорії вібротранспортування відображається моделлю, показаною на рис. 1. Точкова важка частина 1 (перше припущення) рухається по нахиленій під кутом  до горизонту шорсткій площині транспортування 2, що здійснює гармонійні коливання у вертикальній площині за прямолінійною траєкторією під кутом  (кут вібрації) до площини транспортування. Одночасно вважається, що площини коливання і площина транспортування взаємно перпендикулярні. Якщо ввести нерухому систему координат Х¹О¹У¹ і направити вісь О¹Х¹ в площині вібрації, а вісь О¹У¹ - перпендикулярно до площини транспортування, то її коливання по осях О¹Х¹ і О¹У¹ виразяться рівняннями

, , (1)

де А - амплітуда коливання площини транспортування; - кругова частота; - частота коливань.

Рис.1. Модель вібротранспортування

За певних умов отримаємо встановлений рух частинки вздовж осі О¹Х¹ вверх по нахиленій площині, що коливається, з періодично змінною, але постійною середньою швидкістю. В залежності від інтенсивності коливань площини частинка у напрямку осі О¹У¹ або рухається одночасно з площиною транспортування (безвідривний режим), або періодично відривається від неї і здійснює вільний політ (відривний режим).

Рівняння руху частинки в нерухомій системі координат виходячи з діючих на неї сил записується наступним чином

, (2)

, (3)

де т - маса частинки; g - пришвидшення вільного падіння; F- сила опору руху частинки в напрямку О¹Х¹ в контакті з площиною; N- нормальна реакція площини транспортування, що діє на частинку.

Рівняння руху зручно представити в системі координат ХОУ, зв'язаною з площиною, що коливається, тобто в відносних координатах:

(4)

Після подвійного диференціювання цих рівнянь за часом і підстановки в них значень з (1), (2) і (3) отримаємо

, (5)

. (6)

Розглянемо рух частинки в напрямку у. Якщо вона знаходиться в контакті з площиною, то у=0 і тоді (6) матиме вигляд

. (7)

Контакт цей не порушується, тобто N>0, до моменту, доки під час зменшення швидкості площини і частинки виконується умова

. (8)

Ця нерівність випливає з (7) при N>0. Починаючи з деякого моменту t_в (моменту відривання), коли пришвидшення площини стане більшим , її швидкість буде зменшуватись швидше швидкості частинки, що змінюється у відповідності з законом вільного падіння. В цей момент частинка відірветься від лотка і реакція N зникає. При N=0 згідно (7) випливає, що

.

Нерівність (8) і момент відривання зображанні на графіку пришвидшення площини і частинки в нерухомій системі координат (рис.2а). З графіків пришвидшення та очевидно, що відривання може мати місце тільки у випадку .

Ця нерівність може бути представлена у формі

.

Ліву частину позначають

(9)

і називають параметром перевантаження, що показує у скільки разів нормальна складова пришвидшення площини більша нормальної складової пришвидшення вільного падіння. З врахуванням (9) умова відривного режиму матиме вигляд W>1, а безвідривного W≤1. Даний параметр характеризує інтенсивність режиму вібротранспортування.

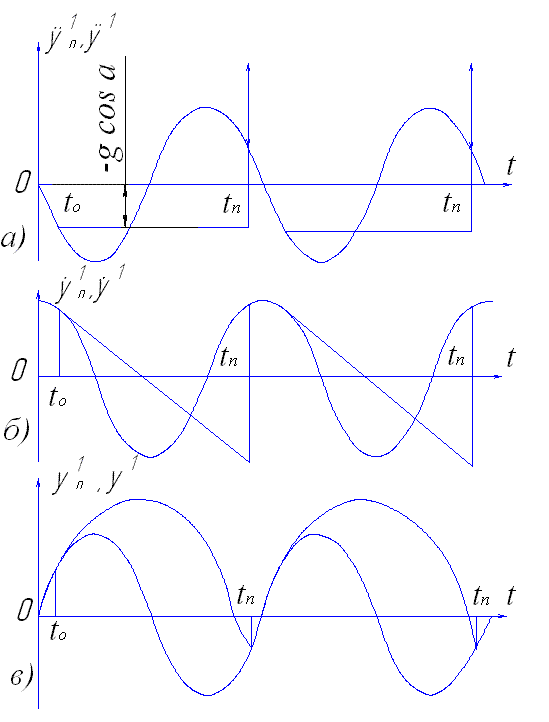
Рис.2

Повздовжня складова амплітуди транспортуючої площини виражається через коефіцієнт перевантаження наступним чином:

.

З моменту відривання t_в триває вільний політ частинки, який в рухомій системі координат описується диференціальним рівнянням:

, (11)

яке отримуємо з рівняння (6) при N=0

Графіки зміни та ,а також та зображені на рис.2,б,в. З рис.2,в видно, що частинка завершає політ падінням на площину в момент t_п (момент падіння).

В момент падіння t_п швидкості частинки і площини, як правило, різні за величиною і можуть бути протилежні за напрямком, отже падіння проходить з ударом. В подальшому удар приймаємо миттєвим і абсолютно непружним (друге припущення), тобто в момент падіння нормальна відносна швидкість частинки миттєво стає рівною нулю:

. (12)

Нормальна швидкість частинки миттєво стає рівною нормальній швидкості лотка , що відповідає ділянці в момент t_п на графіку швидкостей (рис.2,б). В цей момент пришвидшення частинки прямує до безмежності і повертається до величини рівної пришвидшенню лотка (рис.2,а). В подальшому частинка залишається на площині, маючи пришвидшення, швидкість і переміщення останньої аж до моменту нової умови відриву N = 0 (через період).

Розглянемо рух частинки вздовж осі О¹Х¹. Силу опору F руху частинки в момент її проковзування по площині будемо рахувати силою сухого (кулонове) тертя (третє припущення). Це означає, що

(13)

тобто під час проковзування вперед ( ) або назад ( ) сила тертя направлена протилежно швидкості і пропорційна нормальній реакції N. Коефіцієнт пропорційності f є коефіцієнтом тертя-ковзання. У випадку відносного спокою ( ) сила тертя згідно (5) буде рівною

. (14)

При цьому має місце нерівність:

, (15)

яка означає, що модуль сили тертя спокою менший модуля тертя ковзання. Використання в виразах (13) і нерівності (15) одного і того ж коефіцієнта f рівносильне припущенню про рівність коефіцієнтів тертя ковзання і тертя спокою (четверте припущення). Експеримент показує, що звичайно перший з них менший, але врахування цього факту ускладнює методику побудови теорії вібропереміщення.

Ковзання частинки при її контакті з площиною описується рівнянням (5). Після підставлення значення N з (7) у вираз (13) для F і отриманого F з рівняння (5) матимемо:

. (16)

Знак "+" відповідає ковзанню назад, а "-" - ковзанню вперед. Ковзання може продовжуватися до того моменту, доки не виконається умова , тобто поки швидкості площини і частинки не зрівняються. Перехід від стану відносного спокою до ковзання має місце лише при порушенні нерівності (15).

Ковзання може бути перерване і відривом частинки від площини. Її вільний політ в напрямку О¹Х¹ описується диференціальним рівнянням, що отримане з (5) при F=0:

. (17)

Його інтегруванням можуть бути отримані рівняння швидкостей і переміщення в напрямку О¹Х¹ при вільному польоті.

В момент падіння на площину частинка має не тільки нормальну, але і дотичну складову швидкості, яка також змінюється в результаті удару. В теорії вібраційного переміщення часто використовується наступна гіпотеза зміни дотичної складової швидкості (п’яте припущення):

(18)

де та - відносні нормальні дотичні швидкості частинок відповідно після і до удару; f - коефіцієнт ударного тертя.

Перша умова (18) відображає факт удару ковзання, тобто удару, після якого має місце відмінна від нуля швидкість ковзання; друга - умова припинення ковзання.

Розрахунок режиму та середньої швидкості вібротранспортування суттєво спрощується, якщо припустити, що коефіцієнт ударного тертя і коефіцієнт тертя рівні, тобто (шосте припущення).

Рух частинок вверх по площині має встановлений характер. Це означає, що він є строго періодичним з періодом Т, рівним або кратним періоду гармонійних коливань площини. Для 0<<3,724 вказані періоди рівні. Режими вібротранспортування, що характеризуються послідовністю чергування етапів ковзання вперед і назад, сумісного з площиною руху, вільного польоту залежать від параметрів руху А, W, , , f .

Для горизонтально розміщеної площини, що коливається при W >1 характерний режим, який складається з етапу вільного польоту 1 (рис.3), що закінчується ударом з проковзування 2, ковзанням вперед 3 і наступним ковзанням назад 4.

Характер режиму визначається сумісним рішенням рівнянь швидкостей та переміщень, що отримуємо шляхом інтегрування диференціальних рівнянь (11), (16), (І7) з урахуванням зв'язувань цих рівнянь на межах етапів співвідношеннями (12), (18) і обмеження (15), а також умовою періодичності режиму. Середня швидкість V вібропереміщення визначається як відношення шляху S, пройденого частинкою по площині в напрямку О¹Х¹ за період Т, тобто

,

Нехай S отримують інтегруванням швидкості частинки у встановленому режимі за період Т. На графіку швидкості цей шлях відповідає площині, що обмежена кривою швидкості і віссю часу на ділянці Т.

Рис. 3. Режими переміщення деталі

Якщо диференціальні рівняння руху частинки (11), (16) та (17) уявити в безрозмірній формі, розділивши їхні праві та ліві частини на в рівнянні (11) або на в рівняннях (16) і (17), то побачимо, що пришвидшення, а відповідно, швидкість та переміщення частинки залежить від трьох безрозмірних параметрів: перевантаження W, нахилу площини і кута вібрації

(19)

Середню швидкість вібропереміщення зручно представити у наступному вигляді:

, (20)

де k_ш - коефіцієнт швидкості; - максимальна швидкість площини в повздовжньому напрямку. Коефіцієнт швидкості k_ш показує, яку долю максимальної швидкості площини в повздовжньому напрямку складає середня швидкість частинки (викладена теорія дозволяє пов'язувати k_ш з параметрами А, W і k_ .

З рівнянь (11), (16), (17) видно що збільшення кута  призводить до збільшення від'ємного члена і зменшенню додатного , тобто до зменшення швидкості вібротранспортування. Кут при якому швидкість \/=0, називають граничним кутом нахилу площини _гр.

На рис.4 зображені залежності k_ш для різних значень параметра перевантаження W, отримані розрахунками за даною теорією.

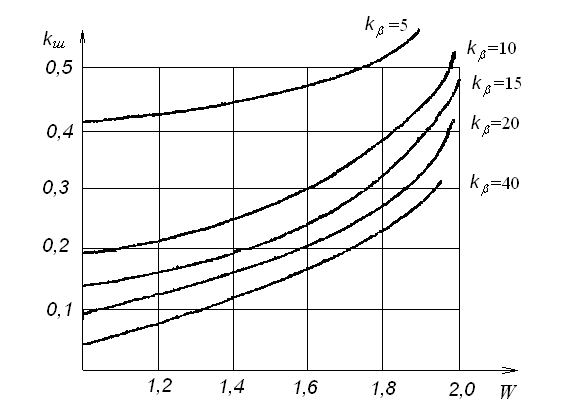
Рис.4. Залежність коефіцієнта швидкості від параметра перевантаження