Многолучевая интерференция световых волн: интерферометр Фабри - Перо

В интерферометре Фабри - Перо (рис. 10.1.0.13) многолучевая интерференция осуществлена многократным отражением пучка параллельных монохроматических световых лучей с λ₀ длиной волны в вакууме от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал. Рассеянный монохроматический свет, в котором имеются световые лучи с λ₀ длиной волны в вакууме самых разнообразных направлений (рис. 10.1.0.13), находящиеся в плоскости рисунка и падающие параллельным пучком на Ппр.З₁ полупрозрачное зеркало под υ₁ углом, после многократного отражения от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал превращаются в n когерентных параллельных световых лучей и собираются по законам геометрической оптики в M₁₁ точке на r₁ расстоянии от FF главной оптической собирающей Л линзы в фокальной плоскости на Э экране, находящегося на

f расстоянии от этой Л собирающей линзы, если эти n когерентных параллельных световых лучей имеют одинаковую оптическую Δ₁ разность хода между собой, кратную целому числу λ₀ длин световых волн в вакууме.

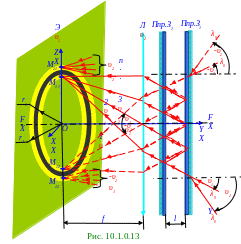
Cветовые лучи с λ₀ длиной волны в вакууме (рис. 10.1.0.13), находящиеся в плоскости рисунка и падающие параллельным пучком на Ппр.З₁ полупрозрачное зеркало под -υ₁ углом, после многократного отражения от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал превращаются в

n когерентных параллельных световых лучей и собираются по законам геометрической оптики в

M₁₂ точке на r₁ расстоянии от FF главной оптической собирающей Л линзы в фокальной плоскости на Э экране, находящегося на f расстоянии от этой Л собирающей линзы, если эти n когерентных параллельных световых лучей имеют одинаковую оптическую Δ₁ разность хода между собой, кратную целому числу λ₀ длин световых волн в вакууме.

Световые лучи с λ₀ длиной волны в вакууме (рис. 10.1.0.13), не находящиеся в плоскости рисунка и падающие параллельным пучком на Ппр.З₁ полупрозрачное зеркало под углом с модулём υ₁, после многократного отражения от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал превращаются в n когерентных параллельных световых лучей и собираются по законам геометрической оптики в точках на окружности r₁ радиусом относительно FF главной оптической собирающей Л линзы в фокальной плоскости на Э экране, находящегося на f расстоянии от этой

Л собирающей линзы, если эти n когерентных параллельных световых лучей имеют одинаковую оптическую Δ₁ разность хода между собой, кратную целому числу λ₀ длин световых волн в вакууме. Таким образом, если параллельные световые лучи с λ₀ длиной волны в вакууме (рис. 10.1.0.13), падающие параллельным пучком на Ппр.З₁ полупрозрачное зеркало под углом с модулём υ₁, после многократного отражения от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал образуют когерентные параллельные световые лучи с Δ₁ оптической разностью хода, удовлетворяющего условию (10.33) интерференционного максимума, то на Э экране образуется светлое кольцо с r₁ радиусом.

Параллельные световые лучи с λ₀ длиной волны в вакууме (рис. 10.1.0.13), падающие параллельным пучком на Ппр.З₁ полупрозрачное зеркало под другим углом с модулём υ₂, после многократного отражения от двух Ппр.З₁, Ппр.З₂ полупрозрачных зеркал превращаются в

n когерентных параллельных световых лучей с Δ₂ оптической разностью хода, удовлетворяющего условию (10.33) интерференционного максимума, вследствие чего на Э экране образуется другое светлое кольцо с r₂ радиусом. В результате на Э экране возникают чередующиеся светлые и тёмные интерференционные кольца с центром в O точке пересечения FF главной оптической собирающей Л линзы с Э экраном, r₁, r₂, …. радиусы которых соответствуют υ₁, υ₂, …. углам падения параллельных лучей, падающих на Ппр.З₁ полупрозрачное зеркало. Эти чередующиеся светлые и тёмные кольца называют интерференционными кольцами равного наклона в интерферометре Фабри - Перо.

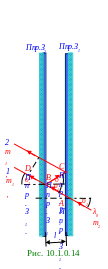
Оптическая Δ разность хода (рис. 10.1.0.14) соседних интерферирующих световых лучей

с λ₀ длиной волной в вакууме определяется следующим выражением:

Δ = ABC - DB = (2l/cosυ) - (2ltqυ sinυ = 2lcosυ. (10.76) Интерференционный максимум (рис. 10.1.0.14) определяется следующим условием (10.33) кратности оптической Δ разности хода (10.76) от соседних интерферирующих когерентных параллельных световых лучей целому числу λ₀ длин волн в вакууме:

2lcosυ = mλ₀ ↔ cosυ = mλ₀/2l ↔ υ = arcos(mλ/2l), (10.77). где m = 1, 2, …- порядок интерференционного максимума, который возрастает по мере уменьшения (рис. 10.1.0.13) υ угла, под которым наблюдают интерференционное кольцо, соответствующее заданному m = 1, 2, … порядку интерференционного максимума.

Угловая D_у дисперсия интерферометра Фабри - Перо - это отношение δυ значения приращения (рис. 10.1.0.3) υ угла, под которым наблюдают интерференционное кольцо, соответствующее заданному m = 1, 2, … порядку интерференционного максимума, при изменении длины световой волны на δλ величину, которая с учётом (10.77) определяется из следующего соотношения:

D_у = δυ/δλ = d(arccosmλ/2l)/dλ ↔ D_у = - {1/[1 - (mλ/2l)²]^1/2}(m/2l) = - m/2lsinυ, (10.78) где (10.77) mλ/2l = cosυ и поэтому [1 - (mλ/2l)²]^1/2 = sinυ.

Из (10.77) получаем следующее выражение: cosυ = mλ/2l ↔ m/2l = cosυ/λ. (10.79)

Подставляем (10.79) в (10.78) и получаем следующее приблизительное выражение, связывающее величину угловую D_у дисперсию интерферометра Фабри - Перо с λ длиной волны в вакууме и

(рис. 10.1.0.3) υ углом падающего параллельного пучка световых лучей на Ппр.З₁ полупрозрачное зеркало: D_у = δυ/δλ = - 1/λtgυ ≈ - 1/λυ, (10.80)

согласно которому при положительном δλ приращении λ длины волны в вакууме и постоянном υ угле падающего параллельного пучка световых лучей на Ппр.З₁ полупрозрачное зеркало, приращение δυ угла υ, под которым наблюдают интерференционное кольцо, соответствующее заданному m = 1, 2, … порядку интерференционного максимума, отрицательно, т.е. при увеличении λ длины волны в вакууме при постоянном υ угле падающего параллельного пучка световых лучей на Ппр.З₁ полупрозрачное зеркало, угол υ, под которым наблюдают на Э экране (рис. 10.1.0.3) интерференционное кольцо, уменьшается.

Это свойство интерферометра Фабри - Перо используется для измерения λ длин волн световых лучей, т.е. для спектральных исследований.

Лекция 14. Дифракция световых волн: принцип Гюйгенса-Френеля. Дифракция световых волн: метод зон Френеля. Дифракция световых волн: радиус зон Френеля. Применение метода зон Френеля в дифракции световых волн от круглого диска: пятно Пуассона. Графический метод расчёта дифракции световых волн от круглого отверстия с помощью спирали Френеля. Графический метод расчёта дифракции световых волн от круглого диска с помощью спирали Френеля. Применение метода зон Френеля в дифракции световых волн от зонной пластинки. Применение метода зон Френеля в дифракции световых волн от пластинки Вуда. Графический метод расчёта дифракции Френеля световых волн от полуплоскости с помощью спирали Корню. Графический метод расчёта дифракции Френеля световых волн от щели в плоскости с помощью спирали Корню. Дифракция Фраунгофера световых волн от круглого отверстия. Дифракция Фраунгофера световых волн от щели в плоскости. Предельный переход от волновой оптики к геометрической.

Дифракция световых волн: принцип Гюйгенса-Френеля

Дифракцией называется совокупность явлений, наблюдаемых при распространении в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Отклонения от законов геометрической оптики при прочих равных условиях оказываются тем меньше, чем меньше длина волны. Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции световых волн.

Перераспределение интенсивности, возникающее в результате суперпозиции световых волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией световых волн.

Перераспределение интенсивности, возникающее вследствие суперпозиции световых волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией световых волн. Поэтому говорят об интерференционной картине от двух узких щелей и о дифракционной картине от одной щели. Согласно принципу Гюйгенса - Френеля каждый (рис. 10.1.0.10) элемент dS волновой поверхности S площадью служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS площадью. Амплитуда dA колебаний A светового вектора

сферической (10.9) световой волны с учётом расстояния r от элемента dS площадью источника сферической световой волны до произвольной М точки пространства имеет следующий вид: dA = ma₀ dS/r, (10.81) где m - коэффициент, зависящий от υ угла между нормалью n к элементу dS площадью и r радиусом - вектором, который соединяет этот элемент dS площадью с произвольной М точкой пространства. При υ = 0 этот

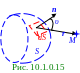
m коэффициент максимален. При υ = π/2 коэффициент m обращается в нуль.

От каждого (рис. 10.1.0.15) элемента dS площадью волновой поверхности S площадью в произвольную М точку пространства приходит колебание A светового вектора сферической световой волны, проекция (10.8) dA которого на плоскость, перепендикулярную r радиусу - вектору, имеет следующий вид: dA = (ma₀ dS/r)cos(ωt - kr + φ₀), (10.82) где (10.81) mA₀ dS/r - амплитуда dA колебаний A светового вектора сферической (10.9) световой волны в произвольной М точке пространства, находящейся на расстояния r от элемента dS площадью источника сферической световой волны в направлении υ угла между n нормалью к этому элементу

dS площадью; Ф = ωt + φ - фаза колебания в произвольный момент t времени на сферической волновой поверхности S площадью; a₀ - множитель, определяемый амплитудой световой волны в том месте, где находится элемент dS площадью на волновой поверхности S площадью; φ - начальная фаза колебания сферической световой волны в момент t₀ = 0 времени в месте расположения волновой поверхности S площадью; ω - циклическая частота колебаний A светового вектора сферической световой волны; k = ω/v - волновое число; v = 1/(ε₀εμ₀μ)^1/2 - фазовая скорость электромагнитной волны, чем являются световые волны с λ₀ длинами волн в вакууме, находящимися в интервале (10.3) 10 нм < λ₀ < 1 мм и распространяющимися в среде с постоянными относительными ε диэлектрической и μ магнитной проницаемостями.

Аналитическое выражение принципа Гюйгенса - Френеля заключается в том, что результирующая проекция A на плоскость, перпендикулярную r радиусу - вектору, A светового вектора сферической световой волны (рис. 10.1.0.15) в произвольной М точке пространства, представляет собой следующую суперпозицию проекций (10.81) dA от всех элементов dS площадью волновой поверхности S площадью: A = ∫dA = ∫(ma₀/r)cos(ωt - kr + φ₀)dS. (10.83) S S

Дифракция световых волн: метод зон Френеля

Точечный источник S создаёт монохроматическую сферическую световую волну в однородной изотропной среде с n показателем преломления, поэтому оптическая λ= λ₀ /n длина этой световой волны совпадает с геометрическими размерами на рис. 10.1.0.16.

Сферическая (2.76) в разделе 02.0.0 "Колебания и волны" волновая поверхность световой волны в произвольный момент времени t имеет a радиус. Если закрыть все зоны кроме 1 - ой с r₁ радиусом, то световые волны, пройдя оптический путь b + λ/2, где λ= λ₀ /n - длина световой волны в однородной изотропной среде с n относительным показателем преломления, будут приходить в M точку пространства на

Э экране в фазе и А амплитуда A светового вектора сферической световой волны в этой M точке пространства на Э экране будет равен А₁.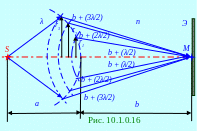

Если в M точку пространства на Э экране будут приходить световые волны от m - зон с r₁, r₂, r₃, … радиусами, то результирующая А амплитуда A светового вектора сферической световой волны в этой M точке пространства будет равна алгебраической сумме А₁, А₃, А₅, … амплитуд, т.е. от зон с нечётными номерами r₁, r₃, r₅, … радиусов и А₂, А₄, А₆, … амплитуд, т.е. от зон с чётными номерами r₂, r₄, r₆, … радиусов.

Все световые волны в M точке пространства от зон с нечётными номерами r₁, r₃, r₅, …радиусов приходят в точку пространства в фазе, т.к. они проходят b + λ/2, b + 3λ/2, b + 5λ/2, …оптические пути, т.е. отличающиеся на λ длину волны. Примем знак их А₁, А₃, А₅, …амплитуд положительным. Все световые волны от зон с чётными номерами r₂, r₄, r₆, … радиусов приходят в M точку пространства в фазе, т.к. они проходят b +2λ/2, b +4λ/2, b + 6λ/2, …оптические пути, т.е. отличающиеся на λ длину волны. Но А₂, А₄, А₆, … амплитуды от зон с чётными номерами r₂, r₄, r₆, … радиусов противоположны по фазе А₁, А₃, А₅, …амплитудам, т.е. от зон с нечётными номерами r₁, r₃, r₅, … радиусов. Поэтому знак А₂, А₄, А₆, … амплитуд является отрицательным.

Результирующая А амплитуда A светового вектора сферической световой волны в M точке пространства (рис. 10.1.0.16) на Э экране от зон с нечётными номерами r₁, r₃, r₅, …радиусов и от зон с чётными номерами r₂, r₄, r₆, … радиусов имеет следующий вид:

А = А₁ - А₂ + А₃ - А₄ + … = (А₁/2) + [(А₁/2) - А₂ + (А₃/2)] +[(А₃/2) - А₄ + (А₅/2)] + … (10.84) В (10.84) слагаемые, являющиеся суммой А амплитуд A светового вектора сферической световой волны в M точке пространства (рис. 10.1.0.16) от соседних зон с нечётными номерами радиусов и от зон с чётными номерами радиусов, имеют следующий вид:

(А₁/2) - А₂ + (А₃/2) ≈ 0, (А₃/2) - А₄ + (А₅/2) ≈ 0, (А₅/2) - А₆ + (А₇/2) ≈ 0, …, (10.85) т.к. А₁, А₃, А₅, … амплитуды, т.е. от зон с нечётными номерами r₁, r₃, r₅, … радиусов, примерно равны А₂, А₄, А₆, … амплитудам от зон с соседними чётными номерами r₂, r₄, r₆, …. радиусов.

Подставляем (10.85) в (10.84): А = А₁ - А₂ + А₃ - А₄ + … ≈ А₁/2, (10.86) из чего следует, что при открытии m - зон Френеля результирующая А амплитуда A светового вектора сферической световой волны в M точке пространства будет меньше амплитуды А₁ при открытой только 1 - ой зоне с r₁ радиусом.

При нечётном количестве открытых зон Френеля, например m = 3, результирующая А амплитуда A светового вектора сферической световой волны в M точке пространства c учётом (10.84) имеет следующий вид:

А = А₁ - А₂ + А₃ = (А₁/2) + [(А₁/2) - А₂ + (А₃/2)] + А₃/2 ≈ (А₁/2) + (А₃/2) > А₁/2. (10.87) При произвольном нечётном m количестве открытых зон Френеля результирующая А амплитуда A светового вектора сферической световой волны в M точке пространства c учётом (10.87) имеет следующий вид: А ≈ (А₁/2) + (А_m /2). (10.88)

При чётном количестве открытых зон Френеля, например m = 4, результирующая

А амплитуда A светового вектора сферической световой волны в M точке пространства c учётом (10.84) имеет следующий вид:

А = А₁ - А₂ + А₃ - А₄ = (А₁/2) + [(А₁/2) - А₂ + (А₃/2)] +[(А₃/2) - А₄] ≈ (А₁/2) + (А₃/2) - А₄ < А₁/2. (10.89) При произвольном m чётном количестве открытых зон Френеля результирующая

А амплитуда A светового вектора сферической световой волны в M точке пространства c учётом (10.89) имеет следующий вид: А ≈ (А₁/2) + (А_m-1 /2) - А_m. (10.90) Амплитуда А_m-1 светового A вектора сферической световой волны в M точке пространства в (10.90) от зоны с нечётным номером r_m-1 радиуса примерно равна А_m амплитуде от зоны с соседним чётным номером r_m радиуса, поэтому имеет место следующее выражение: (А_m-1 /2) - А_m ≈ - А_m/2. (10.91) Подставляем (10.91) в (10.90) и получаем следующую А результирующую амплитуду

A светового вектора сферической световой волны в M точке пространства при произвольном чётном m количестве открытых зон Френеля: А ≈ А₁/2 - А_m/2. (10.92) Сравниваем (10.88) и (10.92), объединяем их в одно выражение и получаем следующую

А результирующую амплитуду A светового вектора сферической световой волны в M точке пространства при произвольном m количестве открытых зон Френеля: А ≈ А₁/2 ± А_m/2, (10.93) где знак "+" берётся при нечётном количестве открытых зон Френеля, а знак "-" берётся при чётном количестве открытых зон Френеля.

Дифракция световых волн: радиус зон Френеля

Радиус (рис. 10.1.0.16) r_m зоны Френеля является катетом двух прямоугольных (рис. 10.1.17) треугольников. Исключением r_m² определяем следующую высоту h_m сферического сегмента m - ой зоны Френеля на сферической волновой поверхности (рис. 10.1.0.17): r_m² = a² - (a - h_m)²

- r_m² = (b + mλ/2)² - (b + h_m)² ↔

↔ h_m = [bmλ + m²(λ/2)²] /2(a + b). (10.94) Ограничившись рассмотрением не слишком больших номеров m зон Френеля, можно ввиду малости λ длины световой волны пренебречь в (10.94) слагаемым, содержащим λ²: h_m ≈ bmλ /2(a + b). (10.95)

b + (mλ/2)

Учтём малость высоты h_m сферического сегмента m - ой зоны Френеля по (рис. 10.1.0.17) сравнению с a радиусом в произвольный момент t времени сферической волновой поверхности, т.е. h_m << a, вследствие чего выражение r_m² = a² - (a - h_m)² принимает следующий вид: r_m² =

= a² - (a - h_m)² = h_m(2a - h_m) ≈ 2ah_m ↔ h_m ≈ r_m ²/2а. (10.96)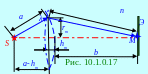

Подставляем (10.95) высоту h_m сферического сегмента m - ой зоны Френеля на сферической волновой поверхности (рис. 10.1.0.17) в (10.96), в результате чего в зависимости от a радиуса сферической волновой поверхности в произвольный момент t времени, расстояния a + b от

S источника световой волны до Э экрана, b расстояния от центра сферической волновой поверхности до (рис. 10.1.0.16), (рис. 10.1.0.17) произвольной М точки пространства, m номера интересующей открытой зоны Френеля и длины λ = λ₀ /n световой волны в однородной изотропной среде с

n показателем преломления получаем следующее выражение r_m радиуса зоны Френеля:

r_m = (abmλ/a+b)^1/2. (10.97)