10.1.0 Волновые свойства света – 4 часа
Лекция 13. Шкала электромагнитного излучения. Уравнение синусоидальной бегущей плоской и сферической световых волн в непоглощающей среде: амплитуда, длина волны, фазовая скорость. Интенсивность синусоидальной бегущей плоской и сферической световых волн в непоглощающей среде. Сложение синусоидальных бегущих плоских некогерентных и когерентных световых волн в непоглощающей среде. Расчет интерференционной картины от одного источника разделением световых волн на две части. Расчет интерференционной картины с двумя когерентными источниками цилиндрических световых волн. Пространственно-временная когерентность световых волн: длина, время и ширина когерентности. Интерференция световых волн в тонких пленках. Интерференционная картина от световых волн равного наклона. Интерференционная картина световых волн с кольцами равной толщины или кольцами Ньютона. Применение интерференции световых волн: интерферометр Майкельсона. Многолучевая интерференция световых волн: интерферометр Фабри - Перо.
Шкала электромагнитных излучений Зависимость λ0 длины волны в вакууме от ν частоты с учётом c фазовой скорости электромагнитных волн в вакууме по аналогии с (2.68) из раздела 02.0 "Колебания и волны" имеет следующий вид: λ0 = c/ν (10.1) Радиоволнами называют электромагнитные волны, λ0 длина волны которых в вакууме с учётом (10.1) связаны следующим соотношением: λ0 > 5·10 -5 м и ν < 6·1012 Гц. (10.2) Оптическим излучением или светом называют электромагнитные волны, λ0 длина волны которых в вакууме находится в следующем интервале: 10 нм < λ0 < 1 мкм, (10.3) где 1 нм = 10 -9 м. К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения. Инфракрасным излучением называют электромагнитное излучение, испускаемое нагретыми телами, λ0 длины волн которых в вакууме находятся в следующем интервале:
770 нм < λ0 < 1 мкм. (10.4) Видимым светом или видимым излучением называют электромагнитное излучение, способное непосредственно вызывать зрительное ощущение в человеческом глазе, с λ0 длинами волн в вакууме, находящихся в следующем интервале: 380 нм < λ0 < 770 нм. (10.5) Ультрафиолетовым излучением называют электромагнитное излучение с λ0 длинами волн в вакууме, находящимися в следующем интервале: 10 нм < λ0 < 380 нм. (10.6) Рентгеновским излучением или рентгеновскими лучами, возникающими при взаимодействии заряженных частиц, а также фотонов с атомами вещества, называют электромагнитное излучение с λ0 длинами волн в вакууме, находящимися в интервале: 0,01. . .1 пм < λ0 < 10. . .100 нм, (10.7) где 1 пм = 10 -12 м.
Уравнение синусоидальной бегущей плоской и сферической световых волн в непоглощающей среде: амплитуда, длина волны, фазовая скорость
В волновой оптике свет представляется электромагнитной волной, поэтому в соответствии с (9.24) из раздела 09.0.0 "Электромагнитные волны" взаимно перпендикулярные векторы E и H напряжённостей соответственно электрического и магнитного полей колеблются с ω циклической частотой в произвольной точке пространства. Плоскость, образованная взаимно перпендикулярными векторами E и H напряжённостей соответственно электрического и магнитного полей в произвольной точке пространства, перпендикулярна к r радиусу - вектору, проведённому из источника световой волны в эту произвольную точку пространства. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями с ω циклической частотой в произвольной точке пространства вектора
E напряжённости электрического поля. В дальнейшем под световым вектором подразумевается вектор E напряжённости электрического поля, а его амплитудное значение обозначается A. Изменение во времени и пространстве A проекции A светового вектора на плоскость, перпендикулярную r радиусу - вектору, проведённому из источника световой волны в произвольную точку пространства, описывается уравнением (9.24) из раздела 09.0.0 "Электромагнитные волны", в котором r радиус - вектор, проведённый из источника световой волны в произвольную точку пространства, направлен по OY оси, вследствие чего эта A проекция A светового вектора на плоскость, перпендикулярную r радиусу - вектору, имеет следующий вид : A = Am cos(ωt - ky + φ), (10.8) где ω - циклическая частота колебаний A светового вектора; k = ω/v (2.70) из раздела 02.0.0 "Колебания и волны" - волновое число, v = с/(εμ)1/2- фазовая (9.10) из раздела 09.0 "Электромагнитные волны" скорость электромагнитной волны в однородной изотропной среде с постоянными относительными ε диэлектрической и μ магнитной проницаемостями; Am - амплитуда колебаний A светового вектора; φ - начальная фаза колебаний A светового вектора.
Для плоской (рис.02.0.17) из раздела 02.0.0 "Колебания и волны" световой волны аналогично плоской бегущей волне для упругой среды (2.69) в разделе 02.0 "Колебания и волны", распространяющейся в непоглощающей среде, амплитуда Am колебаний A светового вектора постоянна, т.е. Am = const.
Для сферической световой волны аналогично сферической бегущей волне для упругой среды (2.76) в разделе 02.0.0 "Колебания и волны", распространяющейся в непоглощающей среде, амплитуда Am колебаний A светового вектора сферической световой волны с учётом r расстояния от источника сферической световой волны до произвольной точки пространства имеет следующий вид: Am = (A0/r), (10.9) где A0 - амплитуда колебаний A светового вектора на r расстоянии, равном единице длины. Для большинства прозрачных веществ, в которых распространяется световая волна, магнитная проницаемость μ ≈ 1, поэтому n показатель преломления этой прозрачной среды, рассчитанный по выражению (9.99) из раздела 09.0.0 "Электромагнитные волны" для определения n показателя преломления среды при распространении электромагнитных волн, принимает следующий вид: n =( ε)1/2, (10.10)
где ε - диэлектрическая проницаемость среды, в которой распространяется электромагнитная волна. Значения n показателя преломления среды из (11.10) характеризуют оптическую плотность среды. Среда с бόльшим n называется оптически более плотной, чем среда с меньшим n. Среда с меньшим n называется оптически менее плотной, чем среда с бόльшим n.
В вакууме световая волна распространяется с v фазовой скоростью, равной скорости c света. Поэтому длина волны λ0 в вакууме с учётом ν частоты колебаний A светового вектора по аналогии с колебаниями (2.68) из раздела 02.0.0 "Колебания и волны" частиц упругой среды имеет следующее значение: λ0 = с/ν = сT, (10.11) где T = 1/ν - период колебаний A светового вектора.
фазовая v скорость (9.10) из раздела 09.0.0 "Электромагнитные волны" световой волны как электромагнитной волны с учётом значения относительной магнитной проницаемости μ ≈ 1 прозрачных веществ, в которых распространяется световая волна, имеет следующее значение:
v = с/(ε)1/2. (10.12) Подставляем (10.10) в (10.12) и получаем следующее выражение, связывающее фазовую (9.10) из раздела 09.0.0 "Электромагнитные волны" v скорость световой волны и n показатель преломления прозрачной среды, в которой распространяется эта световая волна: v = с/n. (10.13) Длина волны λ в прозрачной среде по аналогии с (11.11), а также с учётом ν частоты колебаний A светового вектора в этой среде и фазовой (10.13) v скорости световой волны имеет следующий вид: λ = v/ν = с/νn. (10.14)
Интенсивность синусоидальной бегущей плоской и сферической световых волн в непоглощающей среде
Интенсивность I световой волны в произвольной M точке по аналогии с (9.92) из раздела 09.0 "Электромагнитные волны" интенсивностью электромагнитной волны равняется < S > среднему значению за Δt интервал времени модуля S вектора плотности потока энергии, т.е. вектора S Пойнтинга, в произвольной M точке пространства с r радиусом - вектором, проведённым из источника световой волны в эту произвольную M точку, поэтому эта I интенсивность световой волны имеет следующий вид: I ~ EmHm, (10.15)
где Em и Hm - амплитуды колебаний векторов напряжённостей соответственно E электрического и H магнитного поля световой волны как разновидности электромагнитной волны c λ длинами волн, находящимся в (10.3) интервале.
Согласно (9.28) из раздела 09.0.0 "Электромагнитные волны" отношение Em/Hm амплитуд колебаний векторов E и H напряжённостей соответственно электрического поля и магнитного полей с учётом значения относительной магнитной проницаемости μ ≈ 1 прозрачных веществ, а также с учётом (10.10) n показателя преломления среды, в которых распространяется световая волна, имеет следующий вид: Em/Hm = (μ0/ε0ε)1/2 ↔ Hm = ( ε)1/2(ε0/μ0)1/2 Em = n(ε0/μ0)1/2 Em ↔ Hm ~nEm . (10.16) Подставляем (10.16) в (10.15) с учётом равенства амплитуды Am колебаний A светового вектора величине Em, принятой в (9.24) из раздела 09.0 "Электромагнитные волны" амплитудой колебаний вектора E напряжённости электрического поля электромагнитной волны, и получаем следующее выражение I интенсивности световой волны: I ~ nEm2 = nAm2 ↔ I ~ Am2. (10.17) Согласно (10.17) среднее (9.92) из раздела 09.0.0 "Электромагнитные волны" значение модуля <S > плотности потока энергии или вектора S Пойнтинга за Δt интервал времени, которое называют I интенсивностью электромагнитной и световой волны в произвольной точке пространства, пропорциональна квадрату A2 амплитуды световой волны. Линии, вдоль которых распространяется световая энергия называются лучами. Усреднённый вектор < S > Пойнтинга направлен в каждой точке по касательной к лучу. В изотропных средах направление усреднённого вектора < S > Пойнтинга совпадает с нормалью к волновой поверхности, т.е. с направлением волнового k вектора. Следовательно, световые лучи перпендикулярны к волновым поверхностям.
В естественном свете (рис.
10.1.0.1) колебания A
светового вектора, перпендикулярные
усреднённому вектору
< S
> Пойнтинга, т.е. световому
лучу, например, в произвольные
моменты t1...
t3
времени происходят в различных
направлениях, поэтому векторы
At0...
At3
амплитуды световой волны
в эти
моменты времени направлены в разные стороны.
Естественный свет является неполяризованным светом.
Сложение синусоидальных бегущих плоских некогерентных и когерентных световых волн в непоглощающей среде
Пусть две световые (10.8)
Am1cos(ωt
-
ky
+ φ1),
Am2cos(ωt
-
ky
+ φ2)
волны с одинаковой ω
циклической частотой и Am1,
Am2
амплитудами колебаний A
светового вектора накладываются
друг на друга и возбуждают в фиксированной,
находящейся (рис. 10.1.0.2) на
OY
оси, произвольной
M точке пространства колебания световой волны, усреднённые векторы < S1 >, < S2 > Пойнтинга которых имеют одно направление.
Квадрат Am2 амплитуды световой волны результирующего колебания в (рис. 10.1.2) M точке пространства по аналогии с (2.18) из раздела 02.0.0 "Колебания и волны" определяется следующим сложением двух одинаково направленных гармонических колебаний: Am2 = Am12 +Am22 + 2Am1Am2 cos(Ф2 - Ф1), (10.18)
где (2.69) из раздела 02.0.0 "Колебания и волны" Ф1 = ωt - ky+ φ1 , Ф2 = ωt - ky+ φ2 - фазовые углы колебаний A1, A2 световых векторов первой и второй световых волн в произвольной M точке пространства, имеющей y координату, в данный момент t времени; Ф2 - Ф1 = δ - разность фаз в произвольной M точке пространства, имеющей y координату, колебаний A1, A2 световых векторов первой и второй световых волн в данный момент t времени, равная углу между векторами Am2, Am1 амплитуд этих световых волн.
Если угол δ = Ф2 - Ф1 остаётся (рис. 10.1.0.2) постоянным во времени, что возможно при равенстве ω циклических частот первой и второй световых волн в произвольной M точке пространства, имеющей y координату, то световые волны называются когерентными.
В случае некогерентных световых волн δ = Ф2 - Ф1 угол (рис. 10.1.0.2) между векторами Am2, Am1 амплитуд в M точке пространства непрерывно изменяется с течением t времени, принимая за Δt интервал времени с равной вероятностью любые положительные и отрицательные значения, поэтому <cosδ > = <cos(Ф2 - Ф1)> в случае некогерентных световых волн равно 0.
Таким образом, в случае некогерентных световых волн среднее значение < Am2 > квадрата амплитуды световой волны результирующего колебания в точке (рис. 10.1.0.2) M пространства с учётом (10.18) имеет следующий вид:
< Am2 > = <Am12> + <Am22> + 2<Am1Am2>< cos(Ф2 - Ф1)> = <Am12> + <Am22>. (10.19) Интенсивность I электромагнитной и световой волны согласно (10.17) пропорциональна квадрату Am2 амплитуды световой волны, поэтому (10.19) принимает следующий вид:
I = I1 + I2. (10.20) Согласно (10.20) результирующая I интенсивность электромагнитной и световой волны, наблюдаемая при наложении двух некогерентных световых волн, например, в (рис. 10.1.2) M точке пространства в произвольный момент t времени, равна сумме I1 и I2 интенсивностей, создаваемых каждой световой волной в M точке пространства.
В случае когерентных световых волн cosδ = cos(Ф2 - Ф1) имеет постоянное значение во времени, поэтому результирующая I интенсивность электромагнитной и световой волны согласно (10.18) имеет следующий вид: I = I1 + I2 + 2(I1 I2)1/2cosδ. (10.21) В тех точках пространства, для которых cosδ > 0, результирующая I интенсивность электромагнитной и световой волны согласно (11.21) будет превышать сумму I1 и I2 интенсивностей, создаваемых каждой световой волной в отдельности.
В тех точках пространства, для которых cosδ < 0, результирующая I интенсивность электромагнитной и световой волны согласно (10.21) будет меньше суммы I1 и I2 интенсивностей, создаваемых каждой световой волной в отдельности.
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности.
При равной интенсивности каждой из когерентных световых волн, т.е. когда I1 = I2, в интерференционных (10.21) максимумах при cosδ = 1 результирующая I интенсивность электромагнитной и световой волны имеет следующий вид: I = 4I1. (10.22) В интерференционных (10.21) минимумах, когда cosδ = -1, результирующая I интенсивность электромагнитной и световой волны имеет следующий вид: I = 0. (10.23) Для двух некогерентных световых волн, когда интенсивность обеих световых волн одинакова, т.е. I1 = I2, в любой точке пространства получается всюду одинаковая результирующая
I интенсивность электромагнитной и световой волны, имеющая следующий вид: I = 2I1. (10.24)
Расчет интерференционной картины от одного источника разделением световых волн на две части
Когерентные световые волны получают разделением с помощью отражений или преломлений одной волны, излучаемой одним источником, находящимся (рис. 10.1.0.3) в O точке,
на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их одну на другую, то наблюдается интерференция. Разность оптических путей, проходимых
интерферирующими световыми волнами, не должна быть очень большой.
Световая волна (рис. 10.1.0.3) с вектором Am1 амплитуды колебаний A1 светового вектора проходит геометрический путь l1′ + l1′′ по прозрачной среде с показателем n1 преломления этой среды и направлением светового луча по вектору < S1 > Пойнтинга. В M точке пространства Ф1 фаза колебаний (10.8) этой световой волны c учётом φ01 = 0 начальной фазы колебаний в O точке пространства и ω циклической частоты колебаний A1 светового вектора имеет следующий вид: Ф1 = ωt - k1r1 , (10.25)
где r1
= l1′
+ l1′′
- геометрический путь, который
прошла световая волна с вектором
Am1
амплитуды колебаний
A1
светового вектора; k1
= ω/v1
- волновое число (2.70)
из раздела 02.0.0 "Колебания
и волны"
световой волны, прошедшей r1
= l1′
+ l1′′
геометрический путь с v1
фазовой скоростью. Фазовая
скорость v1
световой волны с вектором
Am1
амплитуды колебаний A1
светового вектора, распространяющейся
в прозрачной среде с n1
показателем преломления,
с учётом (10.13) имеет следующий вид: v1 = c/n1. (10.26) Подставляем (10.26) в (10.25) и получаем (2.69) из раздела 02.0.0 "Колебания и волны" следующую величину Ф1 фазового угла световой волны с вектором Am1 амплитуды колебаний
A1 светового вектора в (рис.11.3) M точке пространства: Ф1 = ωt -[ω(l1′ + l1′′ )/v1 ] = ωt - [ (l1′ + l1′′ )n1ω/c]. (10.27) Аналогично для световой волны (рис. 10.1.0.3) с вектором Am2 амплитуды колебаний
A2 светового вектора, которая проходит геометрический путь l2′ + l2′′ по прозрачной среде с
n2 показателем преломления этой среды и направлением светового луча по вектору
< S2 > Пойнтинга, Ф2 фазовый угол этой световой волны в M точке пространства c учётом начальной φ02 = 0 фазы колебаний в O точке пространства и ω циклической частоты колебаний A2 светового вектора имеет следующий вид: Ф2 = ωt - [ (l2′ + l2′′ )n2ω/c]. (10.28) Разность Ф2 - Ф1 фаз колебаний A2, A1 световых векторов, равный (рис. 10.1.0.2) углу между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент t времени с учётом (10.27), (10.28) имеет следующий вид: Ф2 - Ф1 = (ω/c)[(l2′ + l2′′ ) n2 - (l1′ + l1′′ ) n1]. (10.29) Связь между ν частотой колебаний A светового вектора и его ω циклической частотой имеет следующий вид: ω = 2πν. (10.30) Длина λ0 световой волны в вакууме (10.11) с учётом (10.30) принимает следующий вид: λ0 = 2πс/ω ↔ ω/c = 2π/λ0 . (10.31) Подставляем (10.31) в (10.29), обозначив разность [(l2′ + l2′′)n2 - (l1′ + l1′′)n1] = Δ оптической разностью хода между оптическим L2 = (l2′ + l2′′ )n2 путём световой волны с вектором
Am2 амплитуды колебаний A2 светового вектора и оптическим L1 = (l1′ + l1′′ )n1 путём световой волны с вектором Am1 амплитуды колебаний A1 световых векторов, из чего получаем следующее выражение разности Ф2 - Ф1 фаз колебаний A2, A1 световых векторов, т.е. (рис. 10.1.0.3) δ угол между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент t времени:
Ф2 - Ф1 = δ = (ω/c)[(l2′ + l2′′ ) n2 - (l1′ + l1′′ ) n1] = (2π/λ0 )Δ. (10.32) Если в (10.32) разность Ф2 - Ф1 фаз колебаний A2, A1 световых векторов, т.е. (рис. 10.1.0.3)
δ угол между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент
t времени, кратна 2π, т.е. в (10.18) cos(Ф2 - Ф1) = 1, то в эту M точку пространства в произвольный момент t времени световые волны приходят в одинаковой фазе и в ней поэтому существует интерференционный максимум. Условие кратности 2π разности Ф2 - Ф1 фаз колебаний
A2, A1 световых векторов, т.е. кратности 2π (рис. 10.1.0.3) δ угла между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент t времени с учётом (10.32) приводит к следующему выражению: Ф2 - Ф1 = (2π/λ0 ) Δ = ±m2π ↔ Δ = ± mλ0, (10.33) где m = 0, 1, 2, …. Согласно (10.33) при (рис. 10.1.3) оптической Δ разности хода между оптическим L2 = (l2′ + l2′′)n2 путём световой волны с вектором Am2 амплитуды колебаний A2 светового вектора и оптическим L1 = (l1′ + l1′′)n1 путём световой волны с вектором Am1 амплитуды колебаний
A1 световых векторов, кратным целому числу λ0 длин световых волн в вакууме, в M точке пространства в произвольный момент t времени существует интерференционный максимум. Если в (11.32) разность Ф2 - Ф1 фаз колебаний A2, A1 световых векторов, т.е. (рис. 10.1.0.3)
δ угол между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент
t времени, кратна нечётному количеству ± π, т.е. в (10.18) cos(Ф2 - Ф1) = -1, то в эту M точку пространства в произвольный момент t времени световые волны приходят в противофазе и в ней поэтому существует интерференционный минимум. Условие кратности нечётному количеству
± π разности Ф2 - Ф1 фаз колебаний A2, A1 световых векторов, т.е. кратности π (рис. 10.1.0.3) δ угла между векторами Am2 , Am1 амплитуд в M точке пространства в произвольный момент t времени с учётом (10.32) приводит к следующему выражению:
Ф2 - Ф1 = (2π/λ0 ) Δ = ±(2m + 1)π ↔ Δ = ± (m + 1/2)λ0, (10.34) где m = 0, 1, 2, …. Согласно (10.34) при (рис. 10.1.0.3) оптической Δ разности хода между оптическим L2 = (l2′ + l2′′) n2 путём световой волны с вектором Am2 амплитуды колебаний A2 светового вектора и оптическим L1 = (l1′ + l1′′)n1 путём световой волны с вектором Am1 амплитуды колебаний
A1 световых векторов, кратным нечётному количеству длин световых λ0/2 полуволн в вакууме, в
M точке пространства в произвольный момент t времени существует интерференционный минимум.
Расчет интерференционной картины с двумя когерентными источниками цилиндрических световых волн
Источники (рис. 10.1.0.4)
S1
и S2
- это две тонкие нити, перпендикулярные
плоскости чертежа и находящиеся на d
расстоянии друг от друга, от которых в
рассматриваемую M
точку на Э
экране распространяются световые
лучи с l1,
l2
длинами. Световые волны
в однородной изотропной среде с n
показателем преломления от S1,
S2
источников являются
цилиндрическими, т.е. плоскости
их равных фаз - это окружности с
центрами S1,
S2
точках.
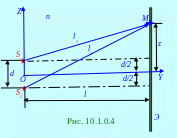
Световые волны от S1, S2 источников являются когрентными.
Оптическая Δ разность хода световых лучей l1, l2 длинами с учётом относительного
n показателя преломления среды, в которой они распространяются, по аналогии с (11.29) имеет следующий вид: n(l2 - l1) = Δ. (10.35)
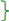Из
геометрии двух прямоугольных
треугольников с l1
и l2
гипотенузами, (x
- d/2)
и (x
+ d/2)
катетами с учётом следующего
приблизительного равенства: l1
+
l2
≈ 2l.
(10.36) приходим
к следующему выражению
связи геометрических параметров,
изображённых на (рис.
10.1.4) схеме:
l22
= l2
+ (z
+ d/2)2
- l12 = l2 + (z - d/2)2 ↔ (l2 + l1)( l2 - l1) = 2zd. (10.37) Подставляем (10.36) в (10.37) и получаем следующее приблизительное выражение, связывающее геометрические параметры на (рис. 10.1.0.4) схеме: ( l2 - l1) ≈ zd/l. (10.38) Умножаем левую и правую части (11.38) на n показатель преломления среды, в которой распространяются световые лучи с l1, l2 длинами, вследствие чего получаем следующее выражение: n( l2 - l1) ≈ nzd/l. (10.39) Подставляем (10.35) оптическую Δ разность хода световых лучей с l1, l2 длинами в (10.39) и получаем её следующую величину для M точки на Э экране, находящейся на z расстоянии от O центра: Δ ≈ nzd/l. (10.40) Для расчёта zmax координат, где будут наблюдаться интерференционные максимумы воспользуемся условием их существования, для чего приравняем (11.33) и (11.40), вследствие чего для расчёта zmax координат получаем следующее выражение:
nzmaxd/l = ± mλ0 ↔ zmax = ± mlλ0/nd ↔ zmax = ± mlλ/d, (10.41) где m = 0, 1, 2, ….; λ = λ0/n - длина световой волны в однородной изотропной среде с n показателем преломления, в которой распространяются световые лучи с l1, l2 длинами.
Для расчёта zmin координат, где будут наблюдаться интерференционные минимумы воспользуемся условием их существования, для чего приравняем (10.34) и (10.40), вследствие чего для расчёта zmin координат получаем следующее выражение:
nzmin d/l = ± (m + 1/2)λ0 ↔ zmin = ± (m + 1/2)l λ0/nd ↔ zmin = ± (m + 1/2)lλ/d, (10.42) где m = 0, 1, 2, ….; λ = λ0/n - длина световой волны в среде с n показателем преломления, в которой распространяются световые лучи с l1, l2 длинами. Расстояние Δzр между соседними интерференционными максимумами (рис. 10.1.0.4), где I интенсивность световой волны максимальна, например, между 1max (m = 1) интерференционным максимумом первого порядка, т.е. в котором оптическая Δ (10.40) разность хода световых лучей с l1, l2 длинами составляет одну длину волны λ = λ0/n в среде с n показателем преломления, и
2max (m = 2) интерференционным максимумом второго порядка, т.е. в котором оптическая Δ (10.40) разность хода световых лучей с l1, l2 длинами составляет две длины волны λ = λ0/n в среде с
n показателем преломления с учётом (10.41), имеет следующий вид: Δzр = z2 max - z1 max = 2lλ/d - lλ/d = lλ/d, (10.43) где Δzр называют расстоянием между интерференционными полосами, которое не зависит от порядка соседних интерференционных максимумов. Для отчётливой интерференционной картины необходимо, чтобы d расстояние между S1, S2 источниками (рис. 10.1.0.4) световых волн было много меньше l расстояния от этих источников световых волн до Э экрана, где наблюдается интерференционная картина.
Расстояние Δzш между соседними интерференционными минимумами (рис. 10.1.0.4), где I интенсивность световой волны минимальна, например, между 1max (m = 1) интерференционным минимумом первого порядка, т.е. в котором оптическая Δ (10.40) разность хода световых лучей с l1, l2 длинами составляет половину длины волны λ/2 = λ0/2n в среде с n показателем преломления, и 2max (m = 2) интерференционным минимумом второго порядка, т.е. в котором оптическая (11.40) Δ разность хода световых лучей с l1, l2 длинами составляет три половины длины волны
3λ/2 = 3λ0 /2n в среде с n показателем преломления с учётом (10.42), имеет следующий вид: Δzш = z2min - z1 min = 3lλ/2d - lλ/2d = lλ/d, (10.44) где Δzш называют шириной интерференционных полос, которое не зависит от порядка соседних интерференционных минимумов. Из сравнения (10.43) и (10.44) следует, что расстояние Δzр между интерференционными полосами равно ширине Δzш интерференционных полос, вследствие чего для расчёта расстояние Δzр между интерференционными полосами и ширины Δzш интерференционных полос получаем следующее выражение: Δzр = Δzш = lλ/d. (10.45)
Пространственно-временная когерентность световых волн: длина, время и ширина когерентности световых волн
Источники (рис. 10.1.0.5) Sλ и Sλ+Δλ - это две тонкие нити, находящиеся в O начале координат и перпендикулярные плоскости чертежа, от которых в рассматриваемую M точку на Э экране распространяются световые лучи. Световые волны с λ, λ+Δλ длинами световых волн в однородной изотропной среде с n показателем преломления от соответственно Sλ, Sλ+Δλ источников являются цилиндрическими, т.е. плоскости их равных фаз - это окружности с центрами Sλ, Sλ+Δλ точках.
Каждый Sλ, Sλ+Δλ источник образует (рис. 10.1.0.5) на Э экране интерференционную картину со следующими значениями Δzλ, Δzλ+Δλ (10.44) ширины интерференционных полос:
Δzλ = lλ/d; Δzλ+Δλ = l(λ+Δλ) /d, (10.46) где λ+Δλ > λ - длины световых волн в однородной изотропной среде с n показателем преломления от соответственно Sλ, Sλ+Δλ источников; d - расстояние между узкими щелями в ДФ диафрагме, находящейся на l расстоянии от Э экрана.
Оптическая Δ (10.40) разность хода в рассматриваемой M точке на Э экране одинакова для интерференционного минимума (m+1)min порядка с λ длиной световой волны и интерференционного максимума mmax порядка с λ+Δλ длиной световой волны, вследствие чего (10.41) для расчёта zm+1 = zm координат получаем следующее выражение:
zm+1 = ± (m+1)lλ/d; zm = ± m(λ+Δλ)lλ/d ↔ ± (m+1)lλ/d ≈ ± m(λ+Δλ)lλ/d ↔ λ ≈ mΔλ, (10.47)
где λ /Δλ = m - степень монохроматичности света; в порядках m > (m+1)min = mmax интерференционные максимумы от световых лучей с λ+Δλ длиной световой волны находятся на
Э экране в z координатах, где существуют интерференционные максимумы от световых лучей с
λ длиной световой волны, и интерференционная картина исчезает.
На рис.
10.1.0.5 приведён пример,
когда интерференционные максимумы,
изображённые красной
штриховкой, от
световых лучей с λ+Δλ
длиной световой волны
перекрывают
интерференционные минимумы,
изображённые зелёной
штриховкой, от
световых лучей с λ
длиной световой волны, вследствие
чего интерференционная картина
исчезает, если m
≥ (m+1)
min
= mmax
. Это означает, что для
примера на
рис. 10.1.0.5 световые волны
от Sλ,
Sλ+Δλ
источников, от которых распространяются
световые лучи,
отличающиеся друг от друга на Δλ длину световой волны, в данной интерференционной системе становятся некогерентными, если m ≥ (m+1) min = mmax . Световые волны от Sλ, Sλ+Δλ источников, от которых распространяются световые лучи, отличающиеся друг от друга на Δλ длину, в данной интерференционной системе будут когерентными до тех пор, пока порядок m интерференционного максимума будет меньше 3, т.е. при значениях порядка m интерференционного максимума, равного m = 0, ±1, ±2.
Оптическая Δ (10.40) разность хода в (рис. 10.1.0.5) рассматриваемой M точке на
Э экране световых лучей с λ, λ+Δλ длинами волн, при распространении которых данная интерференционная система становится некогерентной, имеет с учётом (10.47) следующий вид:
Δ = mmaxλ ≈ λ2/Δλ ↔ lког ≈ λ2/Δλ, (10.48) где lког - длина когерентности световых лучей с λ, λ+Δλ длинами волн, при распространении которых данная интерференционная система при выполнении условия Δ < lког является когерентной. Согласно (10.48) по заданной lког длине когерентности рассчитывают
mmax ≈ λ /Δλ ≈ lког/λ степень монохроматичности света, чтобы в порядке m < mmax интерференционная картина была видна отчётливо в данной интерференционной системе.
Оптическая Δ (10.40) разность хода в (рис. 10.1.0.5) рассматриваемой M точке на
Э экране световых лучей с λ, λ+Δλ длинами волн, при распространении которых данная интерференционная система является когерентной вплоть до m < mmax порядка интерференционного максимума имеет с учётом (10.48) следующий вид:
Δ < mmaxλ ↔ Δ < lког ≈ λ2/Δλ. (10.49) В вакууме lког длину когерентности световой луч с меньшей λ длиной волны из всего диапазона до λ+Δλ значения этих длин волн проходит учётом её c фазовой скорости за следующее tког время когерентности: tког = lког/c ↔ tког ≈ cλ2/Δλ. (10.50)
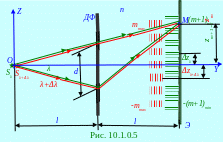
Световые волны с длиной λ волны в однородной изотропной среде с n показателем преломления (рис. 10.1.0.6) от Щ щели бесконечной длины по перпендикулярной плоскости чертежа OX оси и s шириной по OZ оси, находящейся на l расстоянии от ДФ диафрагмы, после прохождения двух узких S1, S2 щелей в ДФ диафрагме, находящихся на d расстоянии друг от друга создают на
Э экране интерференционную картину.
Расстояние d между двумя узкими S1, S2 щелями в ДФ диафрагме, при распространении от которых световые волны становятся некогерентными, обозначают hког шириной когерентности световых волн в данной интерференционной системе, т.е. для определения hког ширины когерентности световых волн имеет место следующее выражение: hког ≈ d, (10.51)
где d - расстояние между двумя узкими S1, S2 щелями в ДФ диафрагме Щ щели, при распространении от которых световые волны становятся некогерентными.
Y
Z
Ппр.З2.
ДФ
При s ширине Щ щели, равной (рис. 10.1.0.6) величине Δz интервала (рис. 10.1.0.6) между интерференционными максимумами 0 порядка от 1, 2 световых лучей, исходящих от ds1, ds2 соответственно верхней и нижней границ Щ щели, будет целиком заполнен при равенстве
l расстояния от Щ щели до ДФ диафрагмы l расстоянию от ДФ диафрагмы до Э экрана интерференционными максимумами 0 порядка от остальных, находящихся между верхней и нижней границами, элементов Щ щели. Поэтому интерференционные полосы исчезнут при следующей
s ширине Щ щели, равной (рис. 10.1.0.6) величине (10.46) Δz интервала между интерференционными максимумами 0 порядка от 1, 2 световых лучей: Δz = lλ/d ↔ s = lλ/d. (10.52)
Подставляем (10.51) в (10.52) и получаем следующее приблизительное выражение, связывающее (рис. 10.1.0.7) hког ширину когерентности световых волн, равное d расстоянию между двумя узкими S1, S2 щелями в ДФ диафрагме, и s шириной Щ щели, при которой интерференционная система когерентна, т.е. при которой интерференционная картина на Э экране будет видна отчётливо:
hког ≈ lλ/s ↔ hког ≈ λ/(s/l) ↔ hког ≈ λ/φ, (10.53)
где φ - малая угловая ширина Щ щели относительно OY оси, проходящей на равных расстояниях от двух узких S1, S2 щелей в ДФ диафрагме.
Интерференция световых волн в тонких пленках
До отражения (рис. 10.1.0.8) в O1 точке 1 световой луч по сравнению со 2 световым лучом проходит в I среде дополнительный d оптический путь, имеющий следующий вид:
d = 2htqυ2 sinυ1. (10.54) Далее световой (рис. 10.1.0.8) луч в вакууме 1 отражается от поверхности среды II с
n2 показателем преломления, оптически более плотной, чем I среда, поэтому в O1 точке отражения 1световой луч меняет свою фазу на π, что эквивалентно прохождению 1 световым лучом оптического пути, равного λ0/2 длины световой волны в вакууме. Поэтому световой 1 луч от плоского O2K волнового фронта, пересекающего 2 луч в O2 точке, проходит оптический l1 путь, имеющий следующий вид: l1 = d + λ0/2 = 2h tqυ2 sinυ1 + λ0/2. (10.55) Световой (рис. 10.1.0.5) луч 2 преломляется в O2 точке, распространяется в II среде с
n показателем преломления до основания тонкой пластины на l расстояние, после чего попадает в
O1 точку.
Оптический (10.29) l2 путь, который прошёл 2 световой луч от плоского O2K волнового фронта до O1 точки при прохождении двойного l расстояния в II среде с n показателем преломления, имеет следующий вид: l2 = 2 n2h/cosυ2 (10.56) Световые (рис. 10.1.0.8) лучи 1 и 2, оказавшись в O1 точке после прохождения соответственно оптических путей l1 (10.55) и l2 (10.56) когерентны, а Δ оптическая разность хода 2′ преломлённого и