42

II начало термодинамики.

Самопроизвольные необратимые процессы всегда ведут к выравниванию интенсивных параметров, в том числе и Т.

Обратимые – процессы, которые при бесконечно малом изменении действующих на систему сил могут идти, как в прямом, так и в обратном направлении, и без изменения работоспособности системы в обоих направлениях. Т.к. действующие силы малы, то такие процессы протекают бесконечно медленно (процессы в гальваническом элементе, все фазовые переходы).

Задача II начала ТД: ответить на вопрос – какие процессы могут идти самопроизвольно?

Формулировки:

1. Кельвин – Планк: невозможен круговой процесс, единственным результатом которого является превращение теплоты в работу (т.е. процесс превращения теплоты в работу необратим);

2. предложена Клаузиусом: Теплота не может переходить сама собой от менее нагретого тела к более нагретому (т.е. процесс теплопроводности необратим);

3. Оствальд: невозможно построить такую периодически действующую машину (вечный двигатель второго рода), все действия которого сводились бы к производству работы и соответствующему охлаждению источника.

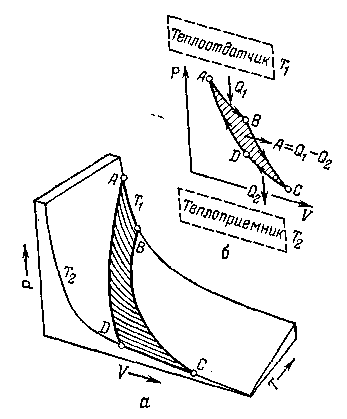
Рисунок. Цикл Карно (а) и термодинамическая схема тепловой машины (б).

Теорема Карно– Клаузиуса:

коэффициент полезного действия машины (КПД) при работе по обратимому циклу не зависит от природы рабочего тела, а определяется только интервалом температур, в котором совершается работа:

.

для элементарного цикла Карно:

или

для бесконечно малого цикла Карно:

или

для конечного цикла Карно

или в пределе может быть заменена интегралом по замкнутому контуру:

, где

– аналитическое уравнение II закона термодинамики

–

фундаментальное уравнение термодинамики

Если процесс необратим, то КПД меньше, чем в обратимом:

;

в пределе , т.е. и .

Неизолированные системы
Обратимые процессы	Необратимые процессы
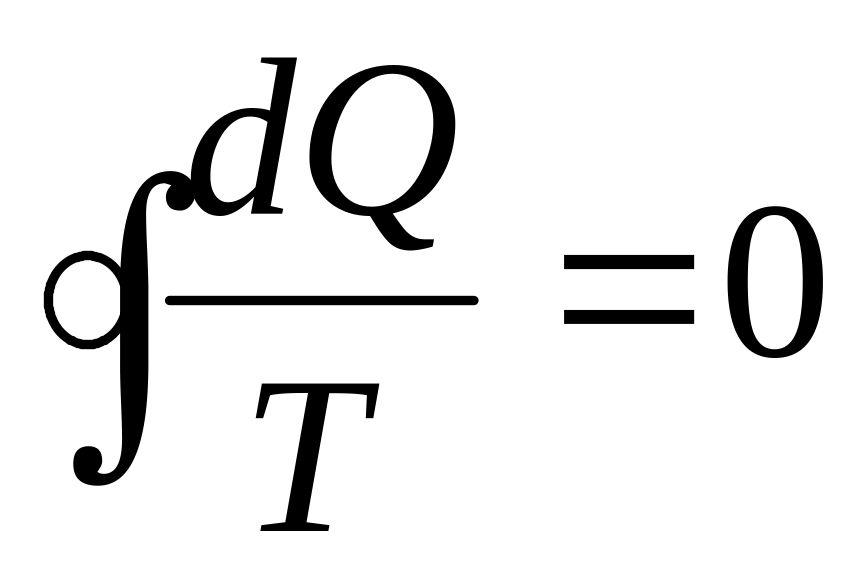
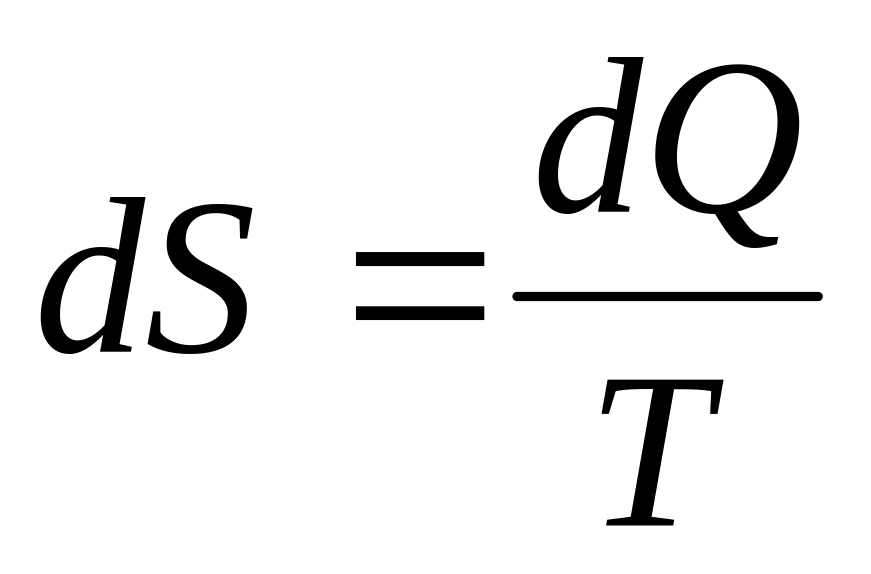
Изолированные системы

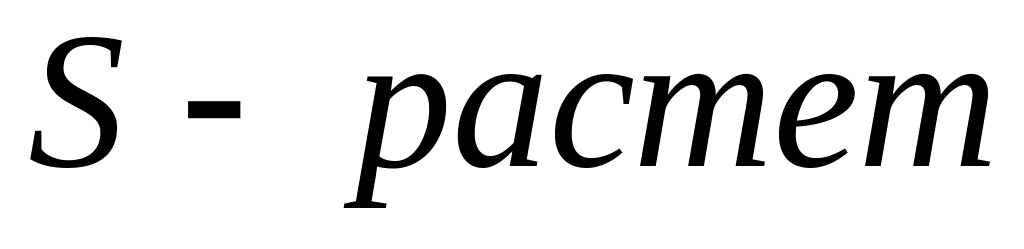
(только при условии U и V=const или H и p=const)

Совместное уравнение первого и второго начала термодинамики:

и .

В изолированных системах:

• всякий самопроизвольный процесс сопровождается возрастанием энтропии,

• этот процесс идет до тех пор, пока система не придет в равновесное состояние, при котором S достигает максимального значения, т.е. при равновесии dS=0,

Равновесное состояние является наиболее вероятным, то, следовательно, энтропия может служить мерой вероятности данного процесса.

Примеры расчетов изменения энтропии идеального газа в различных процессах.

1. изотермическое расширение (сжатие) от начального состояния ( ; ) до конечного состояния ( ; ):

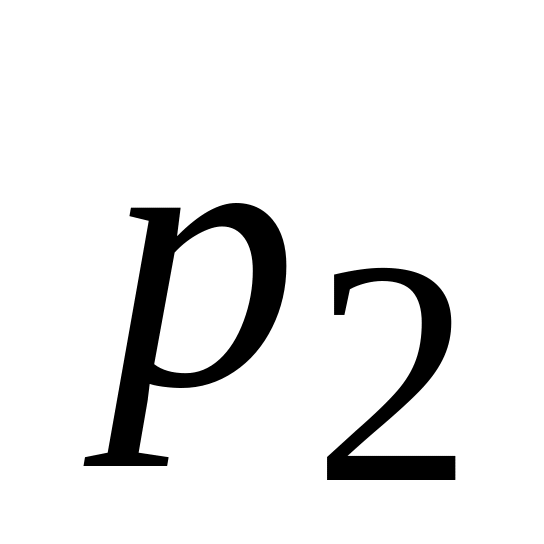Для обратимого процесса:

Т.к. , то , то .

.

.

Пример.

Рассчитайте изменение энтропии в процессе изотермического расширения 10 г криптона от объема 0,05 м³ до объема 0,2 м³ при температуре 500 К.

Решение.

Для решения задачи воспользуемся формулой

.

2. нагревание (охлаждение) без фазового перехода:

в общем случае: .

В случае процесса:

изохорный	изобарный
	Если

.

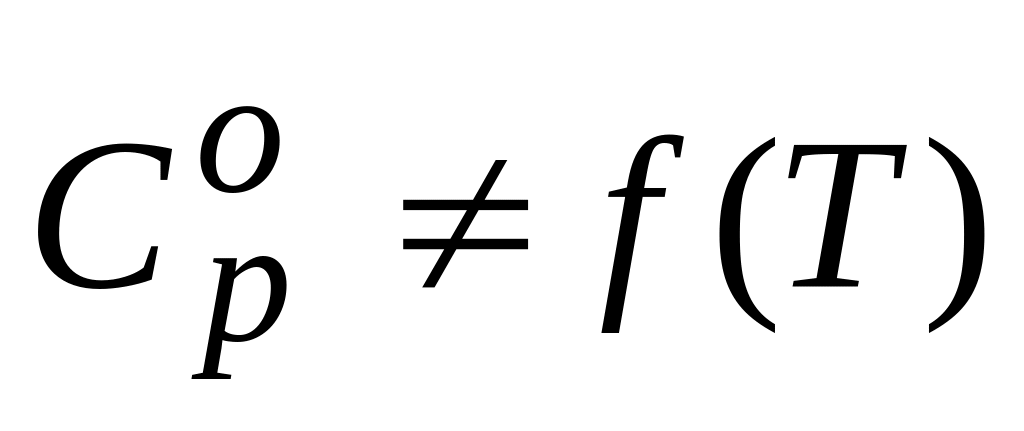
3. Изменение энтропии идеального газа одновременном изменении давления (или объема) системы и температуры:

Пример.

Рассчитайте изменение энтропии, происходящее при расширении до 400 см³ и одновременном нагревании до 50 ºС криптона ( ), содержащегося в контейнере объемом 100 см³ при 25 ºС а давлении Па.

Решение.

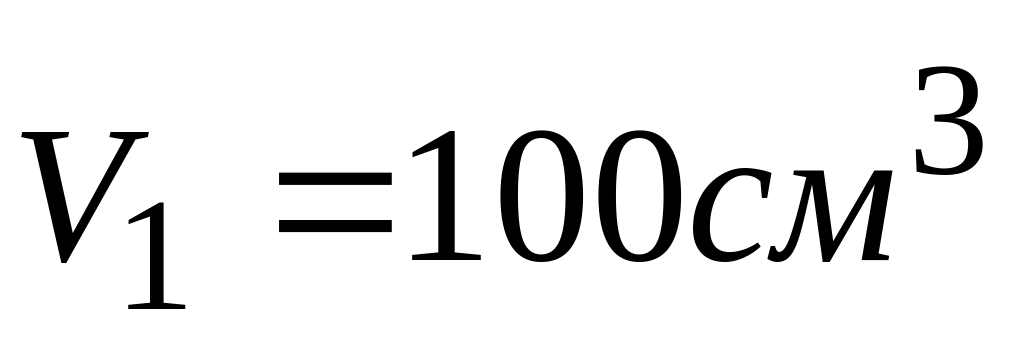
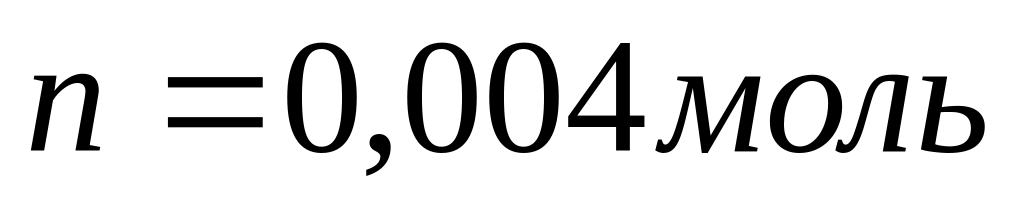
Начальное состояние т.е.		Конечное состояние

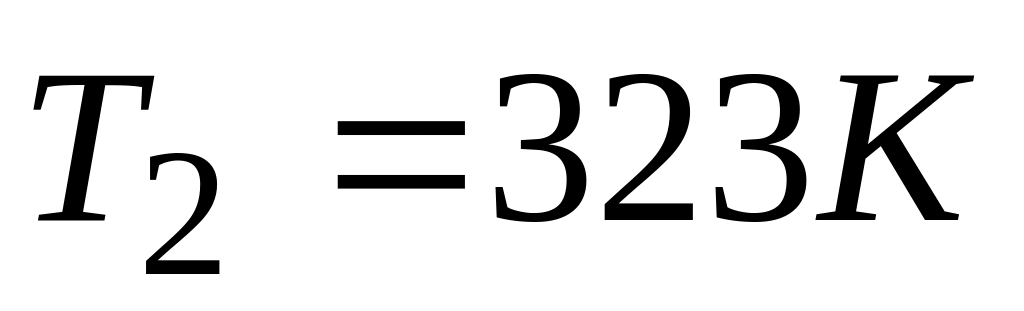
В данном случае систему можно перевести из начального состояния в конечное в две стадии:

• изотермическое расширение от до , при этом ;

• изохорное нагревание от до , при этом .

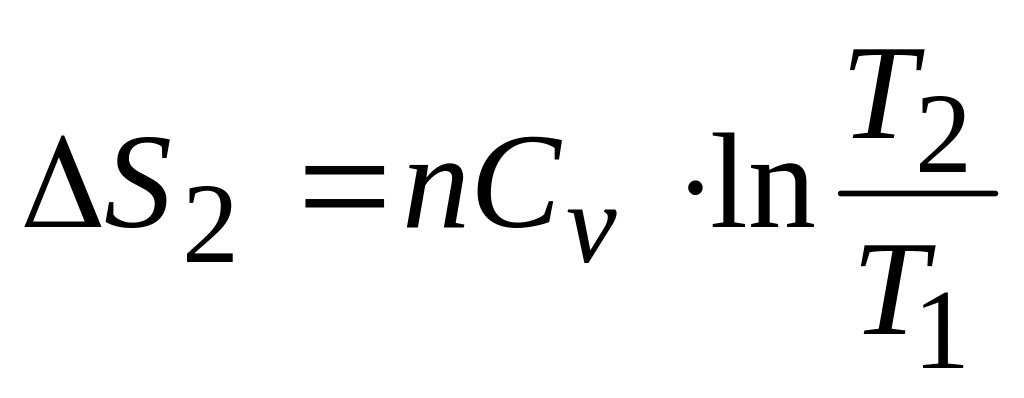Начальное состояние				Конечное состояние
	Изотермическое расширение			Изохорное нагревание
			Промежуточное состояние

Т.е.  .

4. Изменение энтропии идеального газа при фазовом переходе:

где – энтальпия фазового перехода.

Пример.

Рассчитайте изменение энтропии при испарении 0,5 моль метанола ( Па) без учета зависимости теплоемкости от температуры. Нормальная температура кипения метанола равна 64,7 ºС.

Решение.

Процесс испарения метанола ,

.

Для расчетов используем формулу ,

где

.

Выпишем из справочника необходимые данные:

,

Следовательно, .

5. Изменение энтропии в процессе химической реакции.

Пример.

Пользуясь данными таблицы стандартных термодинамических характеристик веществ, определите изменение энтропии химической реакции:

при температурах 400К и 1400К и стандартных исходных давлениях реагентов.

Решение.

Данные для решения задачи берем из справочника:

	S, Дж/(мольК)	Теплоемкость, Дж/(мольК)
		Ср	a
СO	197,55	29,14	28,41	4,1	-0,46
Cl2	222,98	33,93	37,03	0,67	-2,85
COCl2	283,64	57,76	67,15	12,03	-9,04

Рассмотрим два варианта расчета:

• Без учета зависимости теплоемкости от температуры:

(коэффициенты не учитываем, т.к. они все равны единице);

Тогда,

Температура, К	Дж/К Дж/К
400	Дж
1400	Дж

• С учетом зависимости теплоемкости от температуры:

,

где ,

,

т.е. формула для расчета :

,

после интегрирования получаем:

Температура, К	Дж/К Дж/К Дж/К Дж/К
400	Дж
1400	Дж