Графики в логарифмическом и полулогарифмическом масштабе

Для построения графиков функций со значениями х и у, изменяющимися в широких пределах, нередко используют логарифмичес-кие масштабы.

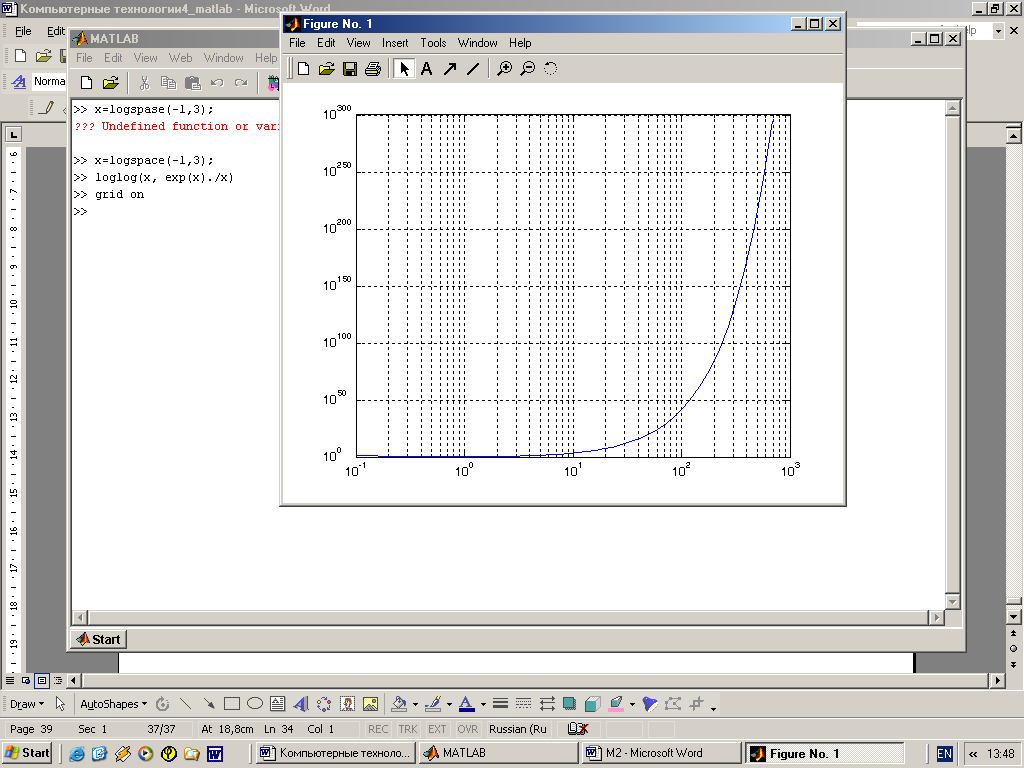
• loglog(. . .) – синтаксис команды анало-гичен ранее рассмотренному для функ-ции plot(. . .). Логарифмический масш-таб используют для координатных осей Х и Y. Ниже дан пример применения данной команды:

>> x=logspace(-1,3);

>> loglog(x, exp(x)./x)

>> grid on

В некоторых случаях предпочтителен полулогарифмический масштаб графиков, ког-да по одной оси задается логарифмический масштаб, а по другой – линейный. Для построения графиков функций в полулогарифмическом масштабе используют следующие команды:

• semilogх(. . .) строит график функции в логарифмическом масштабе (основание 10) по оси Х и линейном по оси Y;

• semilogу(. . .) строит график функции в логарифмическом масштабе по оси Y и ли-нейном по оси Х.

Запись параметров (. . .) выполняется по аналогии с функцией plot(. . .). Например:

>> x=0:0.5:10;

>> semilogy(x, exp(x))

Столбцовые диаграммы

Столбцовые диаграммы широко используются в литературе, посвященной финансам и экономике, а также в математической литературе. Ниже представлены команды для построения таких диаграмм

• bar(X, Y) строит столбцовый график элементов массива Y в позициях, определяемых век-ором Х с упорядоченными в порядке возрастания значений элементами. Если Х и Y – двумерные массивы одинакового размера, то столбцы строятся попарно друг на друге;

• bar(Y) строит график значений одномерного массива;

• bar(X, Y, WIDTH) или bar(Y, WIDTH) – команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH>1 столбцы перекрываются). По умолча-нию задано WIDTH=0.8.

Помимо команды bar(. . .) существует аналогичная ей по синтаксису команда barh(. . .), которая строит столбцовые диаграммы с горизонтальным расположением столбцов.

Построение гистограммы

Классическая гистограмма характеризует число попаданий значений элементов вектора Y в М интервалов с представлением этих этих чисел в виде столбцевой диаграммы. Для получе-ния данных для гистограммы служит функция hist, записываемая в следующем виде:

• N=hist(Y) возвращает вектор чисел попаданий для 10 интервалов, выбираемых авто-матически. Если Y – матрица, то выдается массив данных о числе попаданий для ее столбцов;

• N=hist(Y, М) – аналогична рассмотренной выше, но используется М интервалов (М – скаляр);

• N=hist(Y, Х) возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора Х;

• [N, X]=hist(. . .) возвращает числа попаданий в интервалы и данные о центрах интервалов.

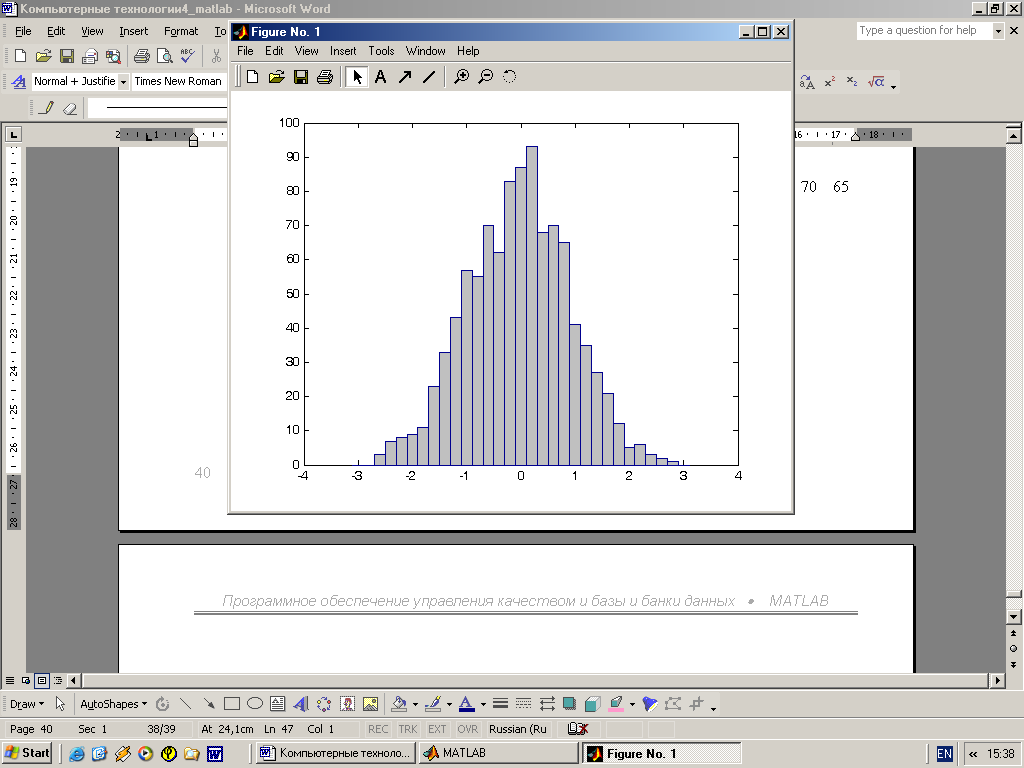
Команда hist с синтаксисом, аналогичным приведенному выше, строит график гистог-раммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором Х.

>> x=-3:0.2:3;

>> y=randn(1000, 1);

>> hist(y,x)

>> h=hist(y,x)

h =

Columns 1 through 20

0 0 3 7 8 9 11 23 33 43 57 55 70 62 83 87 93 68 70 65

Columns 21 through 31

41 35 27 21 12 5 6 3 2 1 0

л а б о р а т о р н а я р а б о т а № 10

1. Введите вектора х и у одинакового размера.

2. Постройте график у(х) в декартовой системе координат.

3. Закажите зеленый цвет полученного графика.

4. Замените сплошную линию на штрих-пунктирную.

5. Отметьте узловые точки графика звездочками.

6. Цвет звездочек замените на красный.

7. Постройте четыре кривые на одном графике с различными спецификациями для каждой кривой.

8. Введите две матрицы одинакового размера.

9. По введенным матрицам также постройте график в декартовой системе координат.

10. Постройте график по произвольным данным в логарифмическом масштабе.

11. По этим же данным постройте график в полулогарифмическом масштабе так, чтобы ось Х была линейной.

12. Этот же график постройте так, чтобы ось Y была линейной.

13. Введите одномерные массивы А и В, состоящие из 8 элементов.

14. Постройте по этим данным столбцовую диаграмму.

15. Замените ширину столбцов на 1.5.

16. Замените полученную диаграмму на диаграмму с горизонтальным расположением столбцов.

17. Получите вектор, состоящий из 2000 случайных чисел.

18. Постройте по этим данным гистограмму.

19. Получите вектор, содержащий число попаданий в 15интервалов.

20. Получите данные о центрах интервалов.

Л е к ц и я № 21, 22

Графика MATLAВ. Двухмерные графики. Создание массивов данных для трехмерной графики

Лестничные графики

Л

естничные графики визуально представляют собой ступеньки с огибающей, представ-ленной функцией у(х). Такие графики используются, например, для отображения процессов квантования функции у(х), представленной рядом своих отсчетов. При этом в промежутках между отсчетами значения функции считаются пос-тоянными и равными величине последнего отчета.

Для построения лестничных графиков в сис-теме MATLAB используются команды группы stairs:

• stairs(Y) строит лестничный график по данным вектора Y;

• stairs(Х, Y) строит лестничный график по дан-ным вектора Y с координатами х переходов от ступеньки к ступеньке, заданными значениями элементов вектора Х;

• stairs(. . ., S) аналогична по действию вышеопи-санным командам, но строит график линиями, стиль которых задается символами S.

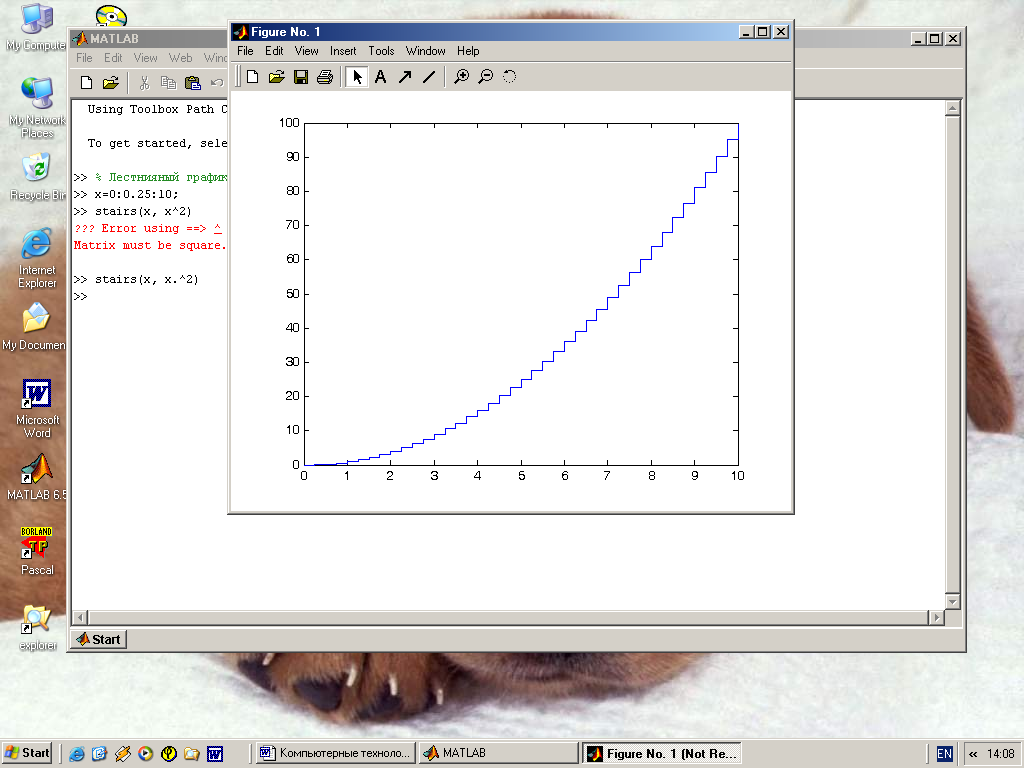
Следующий пример иллюстрирует построение лестничного графика

>> % Лестничный график функции x^2

>> x=0:0.25:10;

>> stairs(x, x.^2)