Упражнения по написанию служебных записок
Напишите служебную записку вашему новому сотруднику Джун Фарбер, в которой вы кратко описываете смысл и значение пооперационного перечня работ для планирования проекта.
Вас направили работать в специальном проекте вне вашего отдела в течение следующих двух лет. При этом не было определено, будет ли это назначение на полную ставку или по совместительству. Напишите докладную записку вашему начальнику, Генри Армбрустеру, с описанием ваших сомнений по каждому виду назначения.
Решение задач
ЗАДАЧА 1
Следующая таблица содержит информацию о главных действиях исследовательского проекта. Используйте эту информацию, чтобы сделать следующее:
Составить диаграмму предшествования.
Найдите критический путь.
Определите ожидаемую продолжительность проекта.
Действие |
Последующее действие |
Предполагаемое время (дни) |
a b c d e f i j g h k |
c, b d i i f j j Конец h k Конец |
5 8 2 7 3 6 10 8 1 2 17 |
Решение:
При построении сетей могут быть полезны следующие наблюдения:
Действия, у которых нет предшественников, располагаются в начале сети (левая сторона).
Действия с несколькими предшествующими размещены на пересечении пути. Начните сетевую диаграмму с определения всех действий без предшественников:
Затем последовательно завершите диаграмму. Пройдите сверху вниз список действий, чтобы ни одно не пропустить. Этот процесс показан на следующей диаграмме
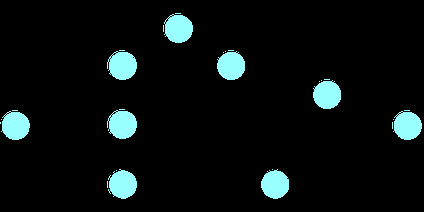
Вот несколько дополнительных подсказок для построения диаграммы предшествования:
Пользуйтесь карандашом.
В начале и конце диаграммы должен быть один узел.
Избегайте пересечения путей.
Нумеруйте узлы слева направо.
Направляйте действия слева направо.
Используйте только одну стрелку между любой парой узлов.
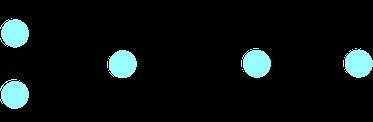
и в).
Путь |
Длина (дни) |
a-c-d-i-j* a-b-i-j e-f-j g-h-k |
5 + 8 + 2 + 10 + 8 = 33** 5 + 7 + 10 + 8 = 30 3 + 6 + 8 = 17 1 + 2 + 17 = 20 |
* Критический путь ** Предполагаемая продолжительность проекта |
|
ЗАДАЧА 2
Используя алгоритм вычисления, определите резервное время для следующей диаграммы. Определите действия, которые находятся на критическом пути.
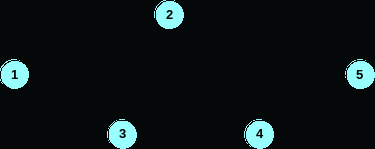
Решение:
Определение времени ES, EF, LS и LP можно значительно упростить, установив две скобки для каждого действия, как это показано ниже:
Левая скобка для каждого действия будет заполнена самым ранним и самым поздним начальным временем, а правая скобка для каждого действия будет заполнена самым ранним и самым поздним конечным временем:
Все это выполняется в два этапа. Сначала определяем самое раннее начальное и самое раннее конечное время, действуя слева направо, как показано в следующей диаграмме.
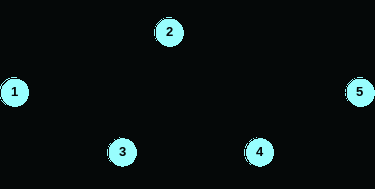
Таким образом, 0 — это начало действия 1 -2. Со временем действия = 4, это действие может быть закончено в 0 + 4 = 4. Это устанавливает самое раннее начальное время для всех действий, которые начинаются в узле 2. Следовательно, 2-5 и 2-4 могут начаться не ранее, чем время 4. Действие 2-5 имеет раннее время окончания 4 + 6 = 10, а действие 2-4 имеет раннее время окончания 4 + 2 = 6. На данном этапе невозможно сказать, каким будет самое раннее начало для действия 4-5: это будет зависеть от того, какое действие — 3-4 или 2-4 — имеет более позднее EF. Следовательно, необходимо вычислить ES и EF по нижнему пути. При ES = 0 для действия 1 -3, его EF = 9, поэтому действие 3-4 будет иметь ES = 9 и EF = 9 + 5 = 14. Учитывая, что два действия, входящие в узел 4, имеют время EF соответственно 6 и 14, самый ранний момент, когда может начаться действие 4-5, равен большему из этих значений, т.е. 14. Следовательно, действие 4-5 имеет ES = 14 и EF = 14 + 3 = 17. Теперь сравним время EF действий, входящих в конечный узел. Самое большее из них 17. Это ожидаемая продолжительность проекта. Теперь можно определить время LF и LS для каждого действия, двигаясь назад по сети (справа налево). LF для двух действий, входящих в узел 5, будет равно 17, т.е. продолжительности проекта. Другими словами, для завершения проекта через 17 недель, эти последние два действия должны закончиться к этому сроку. В случае действия 4-5 LS, необходимое, чтобы LF = 17, будет 17 – 3 = 14. Это значит, что действия 2-4 и 3-4 должны закончиться не позже, чем через 14 недель. Следовательно, их время LF = 14. Действие 3 имеет время LS = 14 – 5 = 9, при этом для действия 1-3 LF = 9 и LS = 9 – 9 = 0.
Действие 2-4, с временем LF = 14, имеет время LS = 14 – 2 = 12. Действие 2-5 имеет LF = 17 и, следовательно, LS = 17 – 6 = 11. Таким образом, самый поздний срок для начала действия 2-5 LS = 11, и для действия 2-4 LS = 12, чтобы эти действия закончились к 17 неделе. Так как действие 1-2 предшествует обоим этим действиям, то оно должно закончиться не позже, чем меньший из этих показателей, т.е. 11. Следовательно, действие 1-2 имеет LF = 11 и LS = 11 – 4 = 7. Времена ES, EF, LF и LS показаны на следующей диаграмме.
Резервное время для любого действия — это разница между любыми LF и EF или LS и ES. Таким образом,
Действие |
LS |
ES |
Резерв |
или |
LF |
EF |
Резерв |
1-2 2-5 2-4 1-3 3-4 4-5 |
7 11 12 0 9 14 |
0 4 4 0 9 14 |
7 7 8 0 0 0 |
|
11 17 14 9 14 17 |
4 10 6 9 14 17 |
7 7 8 0 0 0 |
Действия с нулевым резервным временем указывают на критический путь. В этом случае критический путь 1-3-4-5.
При работе с подобными задачами имейте в виду следующее:
Время ES для действий, выходящих из узлов с многими входящими действиями, является наибольшим EF для входящих действий.
Время LF для действий, входящих в узлы со многими выходящими действиями, является наименьшим LS для выходящих действий.
ЗАДАЧА 3
Ожидаемое время и его отклонения для главных действий научно-исследователь-ского проекта показаны в следующей сетевой диаграмме. Определите вероятность, что время завершения проекта будет:
менее, чем 50 недель;
более, чем 50 недель.
Решение:
Рассчитаем среднее значение и стандартное отклонение для каждого пути:
Путь |
Ожидаемое время (недели) |
Стандартное отклонение (недели) |
1-2-5-8 |
16 + 11 + 24 = 51 |
|
1-3-6-8 |
5 + 18 + 26 = 49 |
|
1-3-4-7-8 |
5 + 10 + 14 + 12 = 41 |
|
=1,22
=
0,60
=
0,85Рассчитаем z для каждого пути с указанной длиной. Для любого пути, который имеет значение большее, чем z = +2,50, считайте вероятность завершения до указанного времени 1,00. Используйте
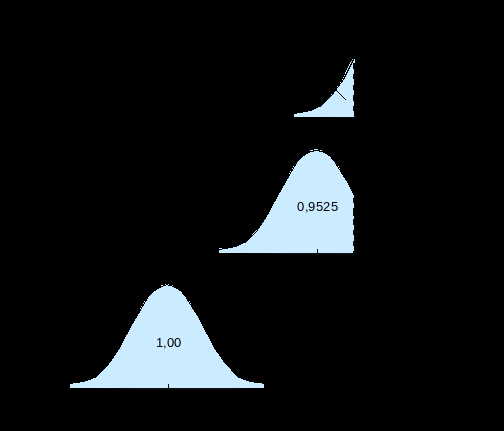
Вероятность, что каждый путь будет закончен через 50 недель или менее, показана в соответствующей диаграмме. (Показатели вероятности взяты из табл. А в приложении). Вероятность, что проект будет закончен через 50 недель или менее, зависит от всех трех путей, которые заканчиваются в это время. Так как z для пути 1-3-4-7-8 больше, чем +2,50, то считается, что вероятность его завершения через 50 недель равна 100%. Менее вероятно, что другие два пути будут закончены за это время. Вероятность, что оба пути не превысят 50 — это произведение их отдельных вероятностей завершения. Таким образом, 0,2061 х 0,9525 = 0,1963.
Вероятность того, что продолжительность проекта будет превышать 50 недель, является разностью этих чисел, которая будет 1,000 – 0,1963 = 0,8037. (Обратите внимание, что это не произведение разностей вероятностей пути.)
ЗАДАЧА 4
Косвенные затраты для проекта — 12 000 долл. в неделю на всем этапе выполнения. Руководитель проекта установил показатели времени и расходов, информация о которых представлена в таблице. Используйте эту информацию, чтобы:
Определить оптимальный план ускорения.
Отобразить графически общие расходы для этого плана.
Действие |
Потенциал ускорения (недели) |
Стоимость ускорения (долл. в неделю) |
а b с d е f |
3 3 2 1 3 1 |
11000 3000 – первая неделя, 4000 – остальные 6000 1000 6000 2000 |
Решение:
(1) Рассчитайте длину путей и определите критический путь:
Путь |
Продолжительность (недели) |
а-b c-d e-f |
24 (критический путь) 19 23 |
(2) Распределите критические действия по расходам на сокращение:
Действие |
Стоимость сокращения (долл. в неделю) |
b а |
3000 11000 |
Действие b нужно сократить на одну неделю, так как с ним связаны меньшие расходы на сокращение. Это уменьшит косвенные расходы на $12000, что обойдется в $3000 — с чистой экономией $9000. На этом этапе оба пути а-b и e-f имеют длину по 23 недели, поэтому оба они будут критическими.
(3) Распределите действия на двух критических путях в соответствии со стоимостью сокращения:
Путь |
Действие |
Стоимость сокращения (долл. в неделю) |
а-b |
b |
4000 |
|
а |
11000 |
e-f |
е |
6000 |
|
f |
2000 |
На каждом пути выберите одно действие (наименее дорогостоящее) для сокращения: действие b на пути а-b и действие f на пути e-f, на общую сумму затрат $4000 + $2000 = $6000 и чистой экономией средств $12000 – $6000 = $6000.
(4) Проверьте, какой путь (пути) будет критическим: длина а-b и e-f no 22 недели, длина c-d по-прежнему 19 недель.
(5) Распределите действия на критических путях:
Путь |
Действие |
Стоимость сокращения ($ в неделю) |
а-b
e-f |
b а е f |
4000 11000 6000 (дальнейшее сокращение невозможно) |
Сокращение действий b на пути а-b и е на пути e-f обойдется в $4000 + $6000 = $10000, при чистой экономии $12000 – $10000 = $2000.
(6) На данном этапе никакое дальнейшее усовершенствование невозможно: пути а-b и e-f имеют продолжительность 21 неделю, и нужно было бы сократить по одному действию на каждом пути. Это означает действие а со стоимостью сокращения $11000 и действие е со стоимостью сокращения $6000 на общую сумму $17000. Эта сумма превышает $12000 потенциальной экономии на косвенных расходах.
Следующая таблица подводит итоги, показывая длительность проекта после сокращения n недель:
Путь |
n=0 |
1 |
2 |
3 |
а -Ь |
24 |
23 |
22 |
21 |
c-d |
19 |
19 |
19 |
19 |
e-f |
23 |
23 |
22 |
21 |
Сокращенное действие |
|
b |
b, f |
b, e |
Стоимость сокращения (в долл.) |
|
3 |
6 |
10 |
В результате мы имеем следующую картину расходов:
Продолжи-тельность проекта |
Общее число сокращенных недель |
Общая стоимость сокращения (долл.) |
Косвенные расходы (долл.) |
Общие расходы (долл.) |
24 23 22 21 20 |
0 1 2 3 4 |
0 3 3 + 6 = 9 9 + 10 = 19 19 + 17 = 36 |
24 х 12 = 288 23 х 12 = 276 22 х 12 = 264 21 х 12 = 252 20 х 12 = 240 |
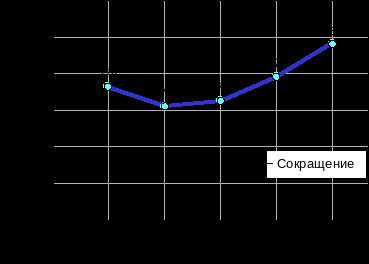
288 279 273 271 276 |
График общих расходов:
ЗАДАЧИ
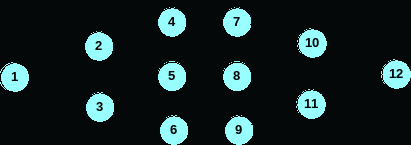
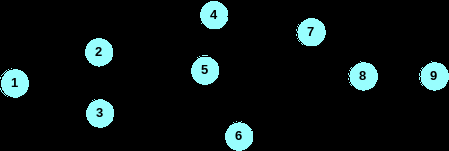
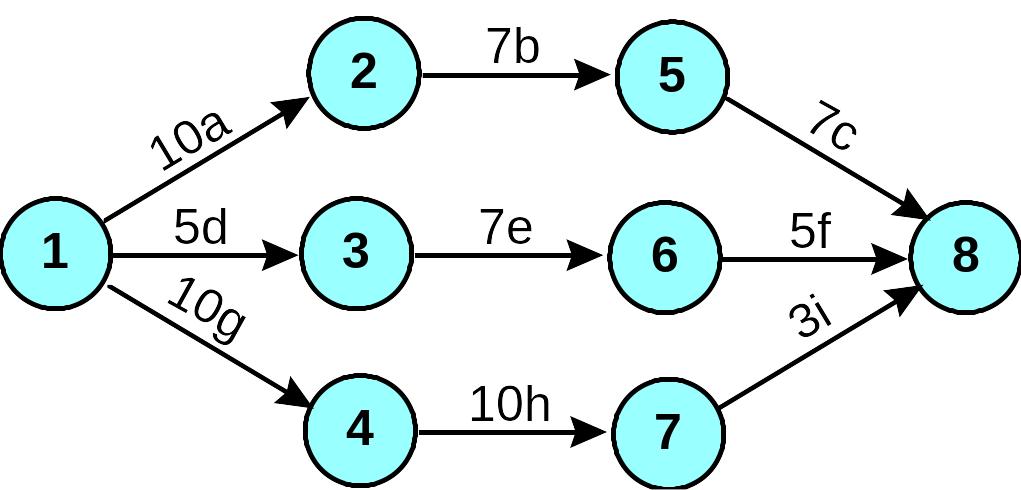
Для каждой из следующих сетевых диаграмм определите критический путь и ожидаемую продолжительность проекта. Числа на стрелке представляют время действия.
Кристине подарили на день рождения новую компьютерную программу. Еще ей подарили чек, на который она собирается купить новый компьютер. Преподаватель колледжа, где учится Кристина, назначил срок сдачи курсовой работы на следующей неделе. Кристина решила, что она подготовит работу на своем новом компьютере. Она составила список действий, которые ей нужно будет сделать, и подсчитала, сколько времени они займут.
Выстройте действия в две логических последовательности.
Постройте сетевую диаграмму, которая будет включать в себя все эти действия.
Определите критический путь и его ожидаемую продолжительность.
По каким причинам проект может потребовать больше времени, чем ожидалось?
Оценка времени (час) |
Действия (с сокращенными обозначениями) |
0,8 0,4 0,2 0,6 0,5
3,0 2,0 1,0 2,0 |
Инсталлировать программу (Inst) Составить план курсовой работы (Out) Представить курсовую работу преподавателю (Sub) Выбрать тему (Сh) Провести проверку орфографии и внести в работу необходимые изменения (Ck) Написать курсовую работу с помощью новой программы (Write) Походить по магазинам и поискать компьютер (Sh) Выбрать и купить компьютер (Sel) Работа над выбранной темой курсовой в библиотеке (Lib) |
Информация в таблице относится к начинающемуся проекту. Как руководитель проекта, на какие действия вы должны обратить особое внимание, с точки зрения завершения проекта в срок? Объясните.
Действие |
Последующее действие |
Оценка времени (дни) |
а |
b |
15 |
b |
с, d |
12 |
с |
е |
6 |
d |
Конец |
5 |
е |
Конец |
3 |
f |
g |
8 |
g |
h |
8 |
h |
j |
9 |
i |
Конец |
7 |
1 |
k |
14 |
k |
Конец |
6 |
Постройте диаграмму предшествования для каждого из следующих случаев. Обратите внимание, что в каждом случае необходимо использовать фиктивное действие.
а. Действие |
Последующее действие |
б. Действие |
Последующее действие |
а |
d |
j |
1, n |
b |
e, f |
k |
r |
с |
g |
i |
m |
d |
k |
m |
Конец |
е |
k |
n |
p |
f |
h, i |
p |
Конец |
g |
i |
q |
s, t |
h |
Конец |
r |
v |
i |
Конец |
v |
v |
k |
Конец |
v |
Конец |
|
|
t |
v, w |
|
|
w |
Конец |
Для каждой из перечисленных задач определите следующие показатели для каждого действия: самое раннее начальное время, самое позднее начальное время, самое раннее конечное время, самое позднее конечное время и резервное время. Назовите критические действия и определите ожидаемую продолжительность проекта.
Задача 1а.
Задача 16.
Задача 1в.
Задача 3.
Пересмотрите сетевую диаграмму задачи 1а. Предположим, что через 12 недель действия 1-2, 1-3 и 2-4 были закончены; действие 2-5 закончено на 75%; и действие 3-6 закончено наполовину. Через сколько недель после исходного начального времени проект будет завершен?
Три выпускника колледжа образовали партнерство и открыли рекламную фирму. Их первый проект состоит из действий, перечисленных в следующей таблице.
|
|
|
Время (дни) |
|
Действие |
Последующее действие |
Оптимисти-ческое |
Наиболее вероятное |
Пессимисти-ческое |
а b с d е f g h i |
с h е f Конец g Конец i Конец |
5 8 6 9 5 5 2 4 5 |
6 8 8 12 6 6 3 4 7 |
7 11 11 15 9 7 7 5 8 |
Постройте диаграмму предшествования.
Какова вероятность, что проект может быть закончен через 24 дня или ранее? Через 21 день или ранее?
Предположим, что сегодня конец седьмого дня; и что действия а и b закончены в то время как действие d — закончено на 50%. Оценки времени для завершения действия d — 5, 6 и 7. Действия с и h готовы к тому, чтобы начаться. Определите вероятность окончания проекта за 24 дня и вероятность его окончания за 21 день.
Новый директор по организационным вопросам в большом университете решил полностью изменить выпускную церемонию. Для этого была разработана сетевая диаграмма для основных действий. Диаграмма имеет пять путей с ожидаемым временем завершения и показателями отклонения, как показано в таблице. Выпускная церемония состоится через 17 недель от настоящего момента. Принимая, что проект начинается немедленно, какова вероятность, что проект будет закончен до:
Дня церемонии выпуска?
Конца недели 16?
Конца недели 13?
Путь |
Ожидаемая продолжительность (недели) |
Дисперсия |
А В С D Е |
10 8 2 15 14 |
2,21 2,00 1,00 2,89 1,44 |
Какова вероятность, что следующий проект потребует для своего завершения больше 10 недель, если средние значения и стандартные отклонения для действий показаны ниже:
Действие |
Среднее значение |
Стандартное отклонение |
1-2 2-3 1-3 |
5 4 8 |
1 1 1 |
Проект, описанный в следующей таблице, только что начался. По плану он должен закончиться через 11 недель.
Если бы вы были руководителем этого проекта, стали бы волноваться в данной ситуации? Объясните.
Если за каждую неделю опоздания с окончанием проекта назначается штраф на сумму $5000, то какова вероятность подвергнуться штрафу по крайней мере в $5000?
Действие |
Оценка времени (недели) |
Стандартное отклонение (недели) |
1-2 2-4 1-3 3-4 |
4 6 3 9 |
0,70 0,90 0,62 1,90 |
Следующая диаграмма предшествования отражает три оценки времени для каждого действия. Определите:
Ожидаемое время завершения для каждого пути и его дисперсию.
Вероятность, что проект потребует больше, чем 49 недель.
Вероятность, что проект можно завершить через 46 недель или ранее.
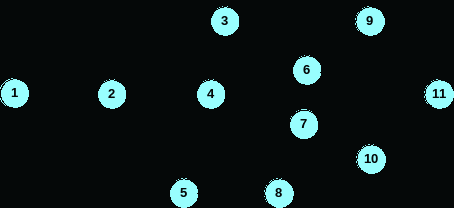
Руководитель проекта составил список основных действий, которые потребуются, чтобы инсталлировать в его компании систему компьютерной информации. Список включает оценки времени выполнения для действий и последовательность связей.
Если проект завершится в пределах 26 недель от начала, руководитель проекта получит премию $1000; если проект закончится в пределах 27 недели от начала, премия будет $500. Найдите вероятность получения каждой премии.
Действие |
Последующее действие |
Оценка времени (недели) |
А |
d, f |
2-4-6 |
D |
е |
6-8-10 |
Е |
h |
7-9-12 |
H |
Конец |
2-3-5 |
F |
g |
3-4-8 |
G |
Конец |
5-7-9 |
B |
i |
2-2-3 |
I |
j |
2-3-6 |
J |
k |
3-4-5 |
K |
Конец |
4-5-8 |
С |
m |
5-8-12 |
M |
n |
1-1-1 |
N |
о |
6-7-11 |
О |
Конец |
8-9-13 |
Постройте A-0-N диаграмму (действие в узле):
для набора действий, приведенных в задаче 3.
Постройте A-0-N диаграмму (действие в узле) для набора действий, перечисленных в задаче 12.
Руководитель проекта целевой группы, планирующей строительство крытого стадиона, надеялся закончить строительство до начала следующего футбольного сезона в колледже. После изучения оценок времени строительства оказалось, что необходимо некоторое ускорение, чтобы гарантировать завершение проекта до начала сезона. Составьте график ускорения с минимальными затратами, чтобы сократить продолжительность проекта на пять недель. Даны следующие оценки времени и расходов:
|
|
|
Стоимость ускорения ($) |
|
Действие |
Последующее действие |
Нормальное время (недели) |
Первая неделя |
Вторая неделя |
A |
b |
12 |
15000 |
20000 |
B |
k |
14 |
10000 |
10000 |
С |
d, e, f |
10 |
5000 |
5000 |
D |
g |
17 |
20000 |
21000 |
Е |
h |
18 |
16000 |
18000 |
F |
i |
12 |
12000 |
15000 |
G |
m |
15 |
24000 |
24000 |
H |
n, p |
8 |
– |
– |
I |
j |
7 |
30000 |
– |
J |
p |
12 |
25000 |
25000 |
K |
Конец |
9 |
10000 |
10000 |
M |
Конец |
3 |
– |
– |
N |
Конец |
11 |
40000 |
– |
Р |
Конец |
8 |
20000 |
20000 |
Общие косвенные расходы строительного проекта — $40 000 в неделю. Главные действия в проекте и их предполагаемые сроки показаны в следующей диаграмме предшествования:
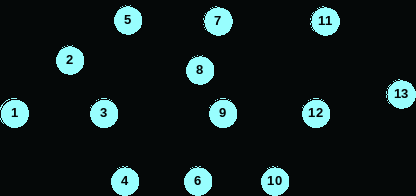
Стоимость ускорения для каждого действия:
|
Стоимость ускорения(долл.) |
||
Действие |
Первая неделя |
Вторая неделя |
Третья неделя |
1-2 |
18 |
22 |
– |
2-5 |
24 |
25 |
25 |
5-7 |
30 |
30 |
35 |
7-11 |
15 |
20 |
– |
11-13 |
30 |
33 |
36 |
1-3 |
12 |
24 |
26 |
3-8 |
– |
– |
– |
8-11 |
40 |
40 |
40 |
3-9 |
3 |
10 |
12 |
9-12 |
2 |
7 |
10 |
12-13 |
26 |
– |
– |
1-4 |
10 |
15 |
25 |
4-6 |
8 |
13 |
– |
6-10 |
5 |
12 |
– |
10-12 |
14 |
15 |
– |
Составьте план ускорения с оптимальным соотношением времени и затрат.
Постройте кривую общих расходов, которая описывает график ускорения с наименьшими затратами, сокращающий продолжительность проекта на шесть недель.
Судостроительная компания Chuck's Custom Boats (CCB) строит роскошные яхты но индивидуальным заказам. CCB заключила контракт с неким таинственным банкиром из Нью-Йорка (господином Т.). Данные по проекту показаны ниже. Сложность заключается в том, что господин Т. хочет получить свою яхту через 32 недели — иначе он будет налагать штраф на сумму $375 за каждую неделю задержки заказа.
Действие |
Последующее |
Нормальное |
Стоимость ускорения ($) |
|
|
действие |
время (недели) |
Первая неделя |
Вторая неделя |
К |
L, N |
9 |
410 |
415 |
L |
М |
7 |
125 |
– |
N |
J |
5 |
45 |
45 |
М |
Q |
4 |
300 |
350 |
J |
0 |
6 |
50 |
– |
0 |
P, Y |
5 |
200 |
225 |
Р |
Z |
8 |
– |
– |
Y |
Конец |
7 |
85 |
90 |
Z |
Конец |
6 |
90 |
– |
Разработайте график ускорения.
Постройте диаграмму Гантта для основных элементов проекта строительства дома, если имеются следующие плановые продолжительности операций:
Поиск места под строительство – 8 недель
Составление плана строительства –2 недели
Одобрение плана владельцем – 2 недели
Закладка фундамента – 8 недель
Возведение стен, крыши – 10 недель
Возведение внутренних перегородок –10 недель
Проведение электрической проводки и водопроводной системы – 4 недели
Установка кухонного оборудования, сантехники – 3 недели
Одобрение плана комитетом по государственному строительству – 2 недели
Подбор рабочих – 2 недели
Подготовка стройплощадки – 2 недели
Внутренние отделочные работы – 4 недели
Поиск поставщиков стройматериалов – 2 недели
Прием построенного дома – 1 неделя
Помогите руководителю маркетинговой службы верно определить длительность проекта (в днях) по выведению нового товара на рынок. Проект представлен в виде диаграммы предшествования.
Для предотвращения принятия решения о банкротстве предприятия руководителю необходимо завершить проект за 90 дней. Проект состоит из основных действий, перечисленных в таблице.
Постройте диаграмму предшествования.
Какова вероятность того, что предприятие будет объявлено банкротом?
Действие |
Последующее |
Время (дни) |
||
|
действие |
Оптимисти- ческое |
Наиболее вероятное |
Пессимисти- ческое |
a |
b |
19 |
23 |
26 |
b |
c |
23 |
30 |
41 |
c |
конец |
19 |
23 |
34 |
d |
e |
34 |
45 |
56 |
e |
c |
8 |
11 |
26 |
f |
g, h |
30 |
30 |
41 |
g |
c |
21 |
25 |
27 |
h |
i |
15 |
15 |
19 |
i |
конец |
19 |
26 |
30 |
Проект строительной организации состоит из основных действий (недели), представленных ниже в виде сетевой диаграммы. В результате посредственной работы отдела по персоналу были набраны недостаточно квалифицированные работники, из-за чего через 43 недели действие 3-6 закончено на 70%, а действие 2-5 завершено на 90%. Что должен предпринять руководитель в данной ситуации (нанять новых работников или оставить старых) при условии, что расходы на прием нового персонала 8000 рублей, а штраф за несдачу проекта в срок 1000 рублей за неделю просрочки. Время для реализации проекта 88 недель. Если руководитель оставляет старых работников, то темп работы сохраняется.
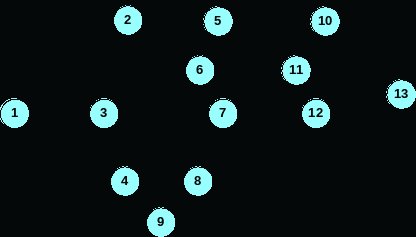
Администрация курортного города решила построить новый пляж для жителей и гостей города. Для этого был разработан проект состоящий из основных действий и представленных в виде сетевой диаграммы. Проект имеет два пути с ожидаемым временем завершения (дни) и показателями отклонения (указанны в скобках) для каждого действия.
Следует ли начинать строительство если до начала пляжного сезона осталось 300 дней?
Какова вероятность того, что строительство закончится за 270 дней?
Кандидату на пост президента компании для победы необходимо реализовать разработанный проект, состоящий из 3-х путей за 12 недель. Средние значения и стандартные отклонения для каждого пути показаны ниже.
Путь |
Среднее значение |
Стандартное отклонение |
A |
10 |
1,6 |
B |
12 |
2,52 |
C |
11 |
2 |
Если бы вы были кандидатом, то стали бы беспокоиться за свою победу? Объясните.
Для успешного завершения семестра студенту необходимо осуществить ряд основных действий, составляющих проект, представленный ниже в виде сетевой диаграммы. Длительность времени на подготовку 120 дней. Какова вероятность того, что студенту не удастся закончить семестр успешно?
Руководитель проекта составил список основных действий, которые необходимы для строительства ресторана. Список представлен в виде диаграммы предшествования. Руководителем принято решение для строительства нанять подрядную фирму, перед которой была поставлена задача закончить строительство за 12 недель. Если проект будет завершен за 10 недель, фирма получит премию 1000$, если на 11 неделе — 500$. В случае не завершения проекта в срок с подрядной фирмы взыскивается неустойка 300$ в неделю. Какова вероятность получения премии 1000$, 500$, вероятность того, что не будет ни премии, ни штрафа?
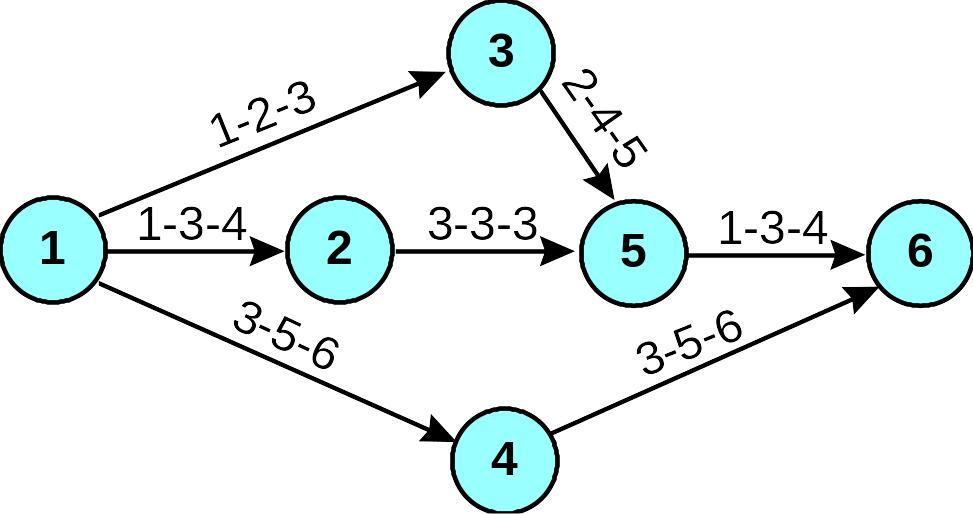
Руководителем маркетинговой службы предприятия были установлены потенциал и стоимость ускорения для основных действий проекта. Уровень косвенных затрат установлен в размере 700$ в неделю. Помогите руководителю определить оптимальный план ускорения.
Действие |
Потенциал ускорения |
Стоимость |
a |
3 |
200 |
b |
2 |
300 |
c |
3 |
400 |
d |
2 |
400 |
e |
2 |
200 |
f |
1 |
300 |
g |
3 |
300 |
h |
1 |
300 |
i |
1 |
400 |
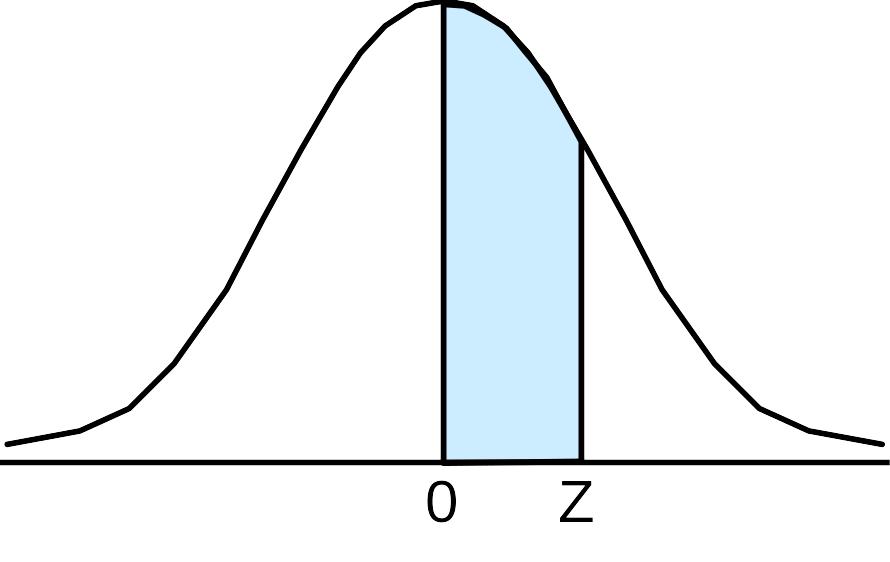
Приложение
Таблица А. Площади под кривой нормального распределения, от 0 до Z
z |
,00 |
,01 |
,02 |
,03 |
,04 |
,05 |
,06 |
,07 |
,08 |
,09 |
0,0 |
,0000 |
,0040 |
,0080 |
,0120 |
,0160 |
,0199 |
,0239 |
,0279 |
,0319 |
,0359 |
0,1 |
,0398 |
,0438 |
,0478 |
,0517 |
,0557 |
,0596 |
,0636 |
,0675 |
,0714 |
,0753 |
0,2 |
,0793 |
,0832 |
,0871 |
,0910 |
,0948 |
,0987 |
,1026 |
,1064 |
,1103 |
,1141 |
0,3 |
,1179 |
,1217 |
,1255 |
,1293 |
,1331 |
,1368 |
,1406 |
,1443 |
,1480 |
,1517 |
0,4 |
,1554 |
,1591 |
,1628 |
,1664 |
,1700 |
,1736 |
,1772 |
,1808 |
,1844 |
,1879 |
0,5 |
,1915 |
,1950 |
,1985 |
,2019 |
,2054 |
,2088 |
,2123 |
,2157 |
,2190 |
,2224 |
0,6 |
,2257 |
,2291 |
,2324 |
,2357 |
,2389 |
,2422 |
,2454 |
,2486 |
,2517 |
,2549 |
0,7 |
,2580 |
,2611 |
,2642 |
,2673 |
,2703 |
,2734 |
,2764 |
,2794 |
,2823 |
,2852 |
0,8 |
,2881 |
,2910 |
,2939 |
,2967 |
,2995 |
,3023 |
,3051 |
,3078 |
,3106 |
,3133 |
0,9 |
,3159 |
,3186 |
,3212 |
,3238 |
,3264 |
,3289 |
,3315 |
,3340 |
,3365 |
,3389 |
1,0 |
,3413 |
,3438 |
,3461 |
,3485 |
,3508 |
,3531 |
,3554 |
,3577 |
,3599 |
,3621 |
1,1 |
,3643 |
,3665 |
,3686 |
,3708 |
,3729 |
,3749 |
,3770 |
,3790 |
,3810 |
,3830 |
1,2 |
,3849 |
,3869 |
,3888 |
,3907 |
,3925 |
,3944 |
,3962 |
,3980 |
,3997 |
,4015 |
1,3 |
,4032 |
,4049 |
,4066 |
,4082 |
,4099 |
,4115 |
,4131 |
,4147 |
,4162 |
,4177 |
1,4 |
,4192 |
,4207 |
,4222 |
,4236 |
,4251 |
,4265 |
,4279 |
,4292 |
,4306 |
,4319 |
1,5 |
,4332 |
,4345 |
,4357 |
,4370 |
,4382 |
,4394 |
,4406 |
,4418 |
,4429 |
,4441 |
1,6 |
,4452 |
,4463 |
,4474 |
,4484 |
,4495 |
,4505 |
,4515 |
,4525 |
,4535 |
,4545 |
1,7 |
,4554 |
,4564 |
,4573 |
,4582 |
,4591 |
,4599 |
,4608 |
,4616 |
,4625 |
,4633 |
1,8 |
,4641 |
,4649 |
,4656 |
,4664 |
,4671 |
,4678 |
,4686 |
,4693 |
,4699 |
,4706 |
1,9 |
,4713 |
,4719 |
,4726 |
,4732 |
,4738 |
,4744 |
,4750 |
,4756 |
,4761 |
,4767 |
2,0 |
,4772 |
,4778 |
,4783 |
,4788 |
,4793 |
,4798 |
,4803 |
,4808 |
,4812 |
,4817 |
2,1 |
,4821 |
,4826 |
,4830 |
,4834 |
,4838 |
,4842 |
,4846 |
,4850 |
,4854 |
,4857 |
2,2 |
,4861 |
,4864 |
,4868 |
,4871 |
,4875 |
,4878 |
,4881 |
,4884 |
,4887 |
,4890 |
2,3 |
,4893 |
,4898 |
,4898 |
,4901 |
,4904 |
,4906 |
,4909 |
,4911 |
,4913 |
,4916 |
2,4 |
,4918 |
,4920 |
,4922 |
,4925 |
,4927 |
,4929 |
,4931 |
,4932 |
,4934 |
,4936 |
2,5 |
,4938 |
,4940 |
,4941 |
,4943 |
,4945 |
,4946 |
,4948 |
,4949 |
,4951 |
,4952 |
2,6 |
,4953 |
,4955 |
,4956 |
,4957 |
,4959 |
,4960 |
,4961 |
,4962 |
,4963 |
,4964 |
2,7 |
,4965 |
,4966 |
,4967 |
,4968 |
,4969 |
,4970 |
,4971 |
,4972 |
,4973 |
,4974 |
2,8 |
,4974 |
,4975 |
,4976 |
,4977 |
,4977 |
,4978 |
,4979 |
,4979 |
,4980 |
,4981 |
2,9 |
4981 |
4982 |
4982 |
4983 |
4984 |
4984 |
4985 |
4985 |
4986 |
4986 |
3,0 |
4987 |
4987 |
4987 |
4988 |
4988 |
4989 |
4989 |
4989 |
4990 |
4990 |
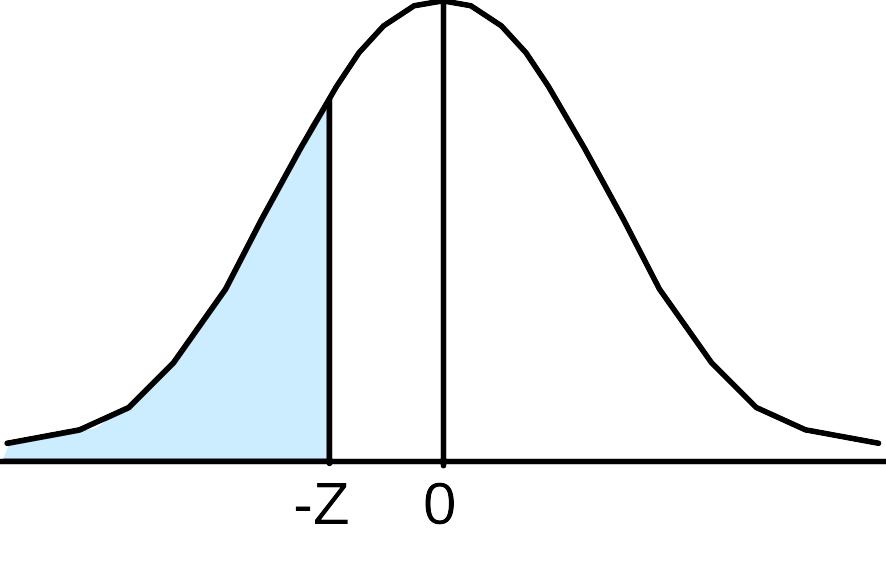
Таблица
Б. Площади под кривой нормального
распределения, от -
до -Z
,09 |
,08 |
,07 |
,06 |
,05 |
,04 |
,03 |
,02 |
,01 |
,00 |
z |
,0002 |
,0003 |
,0003 |
,0003 |
,0003 |
,0003 |
,0003 |
,0003 |
,0003 |
,0003 |
-3,4 |
,0003 |
,0004 |
,0004 |
,0004 |
,0004 |
,0004 |
,0004 |
,0005 |
,0005 |
,0005 |
-3,3 |
,0005 |
,0005 |
,0005 |
,0006 |
,0006 |
,0006 |
,0006 |
,0006 |
,0007 |
,0007 |
-3,2 |
,0007 |
,0007 |
,0008 |
,0008 |
,0008 |
,0008 |
,0009 |
,0009 |
,0009 |
,0010 |
-3,1 |
,0010 |
,0010 |
,0011 |
,0011 |
,0011 |
,0012 |
,0012 |
,0013 |
,0013 |
,0013 |
-3,0 |
,0014 |
,0014 |
,0015 |
,0015 |
,0016 |
,0016 |
,0017 |
,0018 |
,0018 |
,0019 |
-2,9 |
,0019 |
,0020 |
,0021 |
,0021 |
,0022 |
,0023 |
,0023 |
,0024 |
,0025 |
,0026 |
-2,8 |
,0026 |
,0027 |
,0028 |
,0029 |
,0030 |
,0031 |
,0032 |
,0033 |
,0034 |
,0035 |
-2,7 |
,0036 |
,0037 |
,0038 |
,0039 |
,0040 |
,0041 |
,0043 |
,0044 |
,0045 |
,0047 |
-2,6 |
,0048 |
,0049 |
,0051 |
,0052 |
,0054 |
,0055 |
,0057 |
,0059 |
,0060 |
,0062 |
-2,5 |
,0064 |
,0066 |
,0068 |
,0069 |
,0071 |
,0073 |
,0075 |
,0078 |
,0080 |
,0082 |
-2,4 |
,0084 |
,0087 |
,0089 |
,0091 |
,0094 |
,0096 |
,0099 |
,0102 |
,0104 |
,0107 |
-2,3 |
,0110 |
,0113 |
,0116 |
,0119 |
,0122 |
,0125 |
,0129 |
,0132 |
,0136 |
,0139 |
-2,2 |
,0143 |
,0146 |
,0150 |
,0154 |
,0158 |
,0162 |
,0166 |
,0170 |
,0174 |
,0179 |
-2,1 |
,0183 |
,0188 |
,0192 |
,0197 |
,0202 |
,0207 |
,0212 |
,0217 |
,0222 |
,0228 |
-2,0 |
,0233 |
,0239 |
,0244 |
,0250 |
,0256 |
,0262 |
,0268 |
,0274 |
,0281 |
,0287 |
-1,9 |
,0294 |
,0301 |
,0307 |
,0314 |
,0322 |
,0329 |
,0336 |
,0344 |
,0351 |
,0359 |
-1,8 |
,0367 |
,0375 |
,0384 |
,0392 |
,0401 |
,0409 |
,0418 |
,0427 |
,0436 |
,0446 |
-1,7 |
,0455 |
,0465 |
,0475 |
,0485 |
,0495 |
,0505 |
,0516 |
,0526 |
,0537 |
,0548 |
-1,6 |
,0559 |
,0571 |
,0582 |
,0594 |
,0606 |
,0618 |
,0630 |
,0643 |
,0655 |
,0668 |
-1,5 |
,0681 |
,0694 |
,0708 |
,0721 |
,0735 |
,0749 |
,0764 |
,0778 |
,0793 |
,0808 |
-1,4 |
,0823 |
,0838 |
,0853 |
,0869 |
,0881 |
,0901 |
,0918 |
,0934 |
,0951 |
,0968 |
-1,3 |
,0985 |
,1003 |
,1020 |
,1038 |
,1056 |
,1075 |
,1093 |
,1112 |
,1131 |
,1151 |
-1,2 |
,1170 |
,1190 |
,1210 |
,1230 |
,1251 |
,1271 |
,1292 |
,1314 |
,1335 |
,1357 |
-1,1 |
,1379 |
,1401 |
,1423 |
,1446 |
,1469 |
,1492 |
,1515 |
,1539 |
,1562 |
,1587 |
-1,0 |
,1611 |
,1635 |
,1660 |
,1685 |
,1711 |
,1736 |
,1762 |
,1788 |
,1814 |
,1841 |
-0,9 |
,1867 |
,1894 |
,1922 |
,1949 |
,1977 |
,2005 |
,2033 |
,2061 |
,2090 |
,2119 |
-0,8 |
,2148 |
,2177 |
,2206 |
,2236 |
,2266 |
,2296 |
,2327 |
,2358 |
,2389 |
,2420 |
-0,7 |
,2451 |
,2483 |
,2514 |
,2546 |
,2578 |
,2611 |
,2643 |
,2676 |
,2709 |
,2743 |
-0,6 |
,2776 |
,2810 |
,2843 |
,2877 |
,2912 |
,2946 |
,2981 |
,3015 |
,3050 |
,3085 |
-0,5 |
,3121 |
,3156 |
,3192 |
,3228 |
,3264 |
,3300 |
,3336 |
,3372 |
,3409 |
,3446 |
-0,4 |
,3483 |
,3520 |
,3557 |
,3594 |
,3632 |
,3669 |
,3707 |
,3745 |
,3783 |
,3821 |
-0,3 |
,3859 |
,3897 |
,3936 |
,3974 |
,4013 |
,4052 |
,4090 |
,4129 |
,4168 |
,4207 |
-0,2 |
,4247 |
,4286 |
,4325 |
,4364 |
,4404 |
,4443 |
,4483 |
,4522 |
,4562 |
,4602 |
-0,1 |
,4641 |
,4681 |
,4721 |
,4761 |
,4801 |
,4840 |
,4880 |
,4920 |
,4960 |
,5000 |
-0,0 |
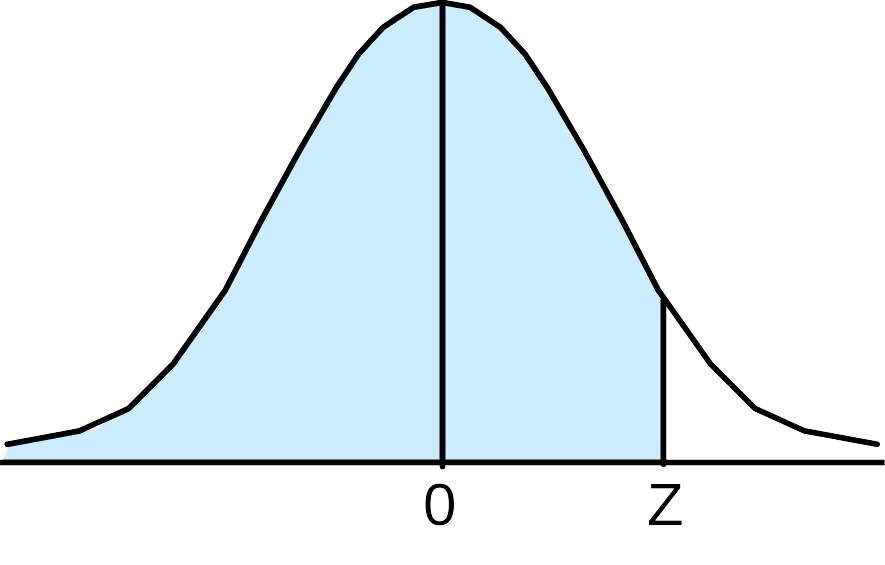
Таблица В. Площади под кривой нормального распределения, от - до +Z
z |
,00 |
,01 |
,02 |
,03 |
,04 |
,05 |
,06 |
,07 |
,08 |
,09 |
,0 |
,5000 |
,5040 |
,5080 |
,5120 |
,5160 |
,5199 |
,5239 |
,5279 |
,5319 |
,5359 |
,1 |
,5398 |
,5438 |
,5478 |
,5517 |
,5557 |
,5596 |
,5636 |
,5675 |
,5714 |
,5753 |
,2 |
,5793 |
,5832 |
,5871 |
,5910 |
,5948 |
,5987 |
,6026 |
,6064 |
,6103 |
,6141 |
,3 |
,6179 |
,6217 |
,6255 |
,6293 |
,6331 |
,6368 |
,6406 |
,6443 |
,6480 |
,6517 |
,4 |
,6554 |
,6591 |
,6628 |
,6664 |
,6700 |
,6736 |
,6772 |
,6808 |
,6844 |
,6879 |
,5 |
,6915 |
,6950 |
,6985 |
,7019 |
,7054 |
,7088 |
,7123 |
,7157 |
,7190 |
,7224 |
,6 |
,7257 |
,7291 |
,7324 |
,7357 |
,7389 |
,7422 |
,7454 |
,7486 |
,7517 |
,7549 |
,7 |
,7580 |
,7611 |
,7642 |
,7673 |
,7703 |
,7734 |
,7764 |
,7794 |
,7823 |
,7852 |
,8 |
,7881 |
,7910 |
,7939 |
,7967 |
,7995 |
,8023 |
,8051 |
,8078 |
,8106 |
,8133 |
,9 |
,8159 |
,8186 |
,8212 |
,8238 |
,8264 |
,8289 |
,8315 |
,8340 |
,8365 |
,8389 |
1,0 |
,8413 |
,8438 |
,8461 |
,8485 |
,8508 |
,8531 |
,8554 |
,8577 |
,8599 |
,8621 |
1,1 |
,8643 |
,8665 |
,8686 |
,8708 |
,8729 |
,8749 |
,8770 |
,8790 |
,8810 |
,8830 |
1,2 |
,8849 |
,8869 |
,8888 |
,8907 |
,8925 |
,8944 |
,8962 |
,8980 |
,8997 |
,9015 |
1,3 |
,9032 |
,9049 |
,9066 |
,9082 |
,9099 |
,9115 |
,9131 |
,9147 |
,9162 |
,9177 |
1,4 |
,9192 |
,9207 |
,9222 |
,9236 |
,9251 |
,9265 |
,9279 |
,9292 |
,9306 |
,9319 |
1,5 |
,9332 |
,9345 |
,9357 |
,9370 |
,9382 |
,9394 |
,9406 |
,9418 |
,9429 |
,9441 |
1,6 |
,9452 |
,9463 |
,9474 |
,9484 |
,9495 |
,9505 |
,9515 |
,9525 |
,9535 |
,9545 |
1,7 |
,9554 |
,9564 |
,9573 |
,9582 |
,9591 |
,9599 |
,9608 |
,9616 |
,9625 |
,9633 |
1,8 |
,9641 |
,9649 |
,9656 |
,9664 |
,9671 |
,9678 |
,9686 |
,9693 |
,9699 |
,9706 |
1,9 |
,9713 |
,9719 |
,9726 |
,9732 |
,9738 |
,9744 |
,9750 |
,9756 |
,9761 |
,9767 |
2,0 |
,9772 |
,9778 |
,9783 |
,9788 |
,9793 |
,9798 |
,9803 |
,9808 |
,9812 |
,9817 |
2,1 |
,9821 |
,9826 |
,9830 |
,9834 |
,9838 |
,9842 |
,9846 |
,9850 |
,9854 |
,9857 |
2,2 |
,9861 |
,9864 |
,9868 |
,9871 |
,9875 |
,9878 |
,9881 |
,9884 |
,9887 |
,9890 |
2,3 |
,9893 |
,9896 |
,9898 |
,9901 |
,9904 |
,9906 |
,9909 |
,9911 |
,9913 |
,9916 |
2,4 |
,9918 |
,9920 |
,9922 |
,9925 |
,9927 |
,9929 |
,9931 |
,9932 |
,9934 |
,9936 |
2,5 |
,9938 |
,9940 |
,9941 |
,9943 |
,9945 |
,9946 |
,9948 |
,9949 |
,9951 |
,9952 |
2,6 |
,9953 |
,9955 |
,9956 |
,9957 |
,9959 |
,9960 |
,9961 |
,9962 |
,9963 |
,9964 |
2,7 |
,9965 |
,9966 |
,9967 |
,9968 |
,9969 |
,9970 |
,9971 |
,9972 |
,9973 |
,9974 |
2,8 |
,9974 |
,9975 |
,9976 |
,9977 |
,9977 |
,9978 |
,9979 |
,9979 |
,9980 |
,9981 |
2,9 |
,9981 |
,9982 |
,9982 |
,9983 |
,9984 |
,9984 |
,9985 |
,9985 |
,9986 |
,9986 |
3,0 |
,9987 |
,9987 |
,9987 |
,9988 |
,9988 |
,9989 |
,9989 |
,9989 |
,9990 |
,9990 |
3,1 |
,9990 |
,9991 |
,9991 |
,9991 |
,9991 |
,9992 |
,9992 |
,9992 |
,9993 |
,9993 |
3,2 |
,9993 |
,9993 |
,9994 |
,9994 |
,9994 |
,9994 |
,9994 |
,9995 |
,9995 |
,9995 |
3,3 |
,9995 |
,9995 |
,9995 |
,9996 |
,9996 |
,9996 |
,9996 |
,9996 |
,9996 |
,9997 |
3,4 |
,9997 |
,9997 |
,9997 |
,9997 |
,9997 |
,9997 |
,9997 |
,9997 |
,9997 |
,9998 |