Значение ресурса

Режим работы	Легкий	Средний	Тяжелый	Очень тяжелый
, ч.	5000	2000	1000	500

Расчетный ресурс должен быть не меньше допустимого ресурса для заданного (принятого) режима работы, т. е. .

Для универсальных и широкоуниверсальных станков, работающих в условиях повышенных нагрузок и вибраций (деформационного упрочнения, наростообразования), принимается тяжелый режим работы, для которого установлена долговечность 1000 ч.

Если критерии долговечности не выполняется, то есть T_о <T_p, необходимо внести коррективы в параметры передачи.

1.Увеличить длину ремня L_p, приняв ближайшее большее значение в стандартном ряду. При этом уменьшается число пробегов ремня и, соответственно, пропорционально увеличивается долговечность T_о. Увеличение L_p потребует перерасчета межосевого расстояния а. Остальные параметры передачи не изменяться.

2.Увеличить диаметр шкивов: взять ближайшее большее d_p1 из стандартного ряда и пересчитать для него новое значение d_p2. В этом случае автоматически возрастает длина ремня L_p (и, как следствие, растет а), что положительно влияет на число пробегов ν, уменьшая его. Однако, одновременно с ростом d_p1 и d_p2 повысится скорость ремня что негативно сказывается на ν, увеличивая его значение. Но в целом, рост L_p будет более существенным, чем прирост V, поэтому результирующие значение ν будет уменьшаться.

Одновременно с этим , увеличение d_p1 вызовет снижение напряжения изгиба в ремне:

,

а значит и σ_max. Этот фактор гораздо в большей степени благоприятно скажется на долговечности, так как T_о и σ_max связаны степенной зависимостью. Так, уменьшение σ_max на 10% вызовет рост T_о примерно на 70% (при прочих равных условиях). Поэтому способ корректировки 2) является более эффективным для повышения долговечности клиновых ремней по сравнению с 1), но сопровождается более существенным увеличением габаритов передачи.

Спроектированная передача считается работоспособной, если выполняются оба расчетных критерия:

σ_max [ σ_p];

T_о T_p.

Сила давления на валы

Расчетная схема к определению силы F давления на вал, где расположен ведущий (малый в данном случае) шкив, представлена на рис. 6.1.4.

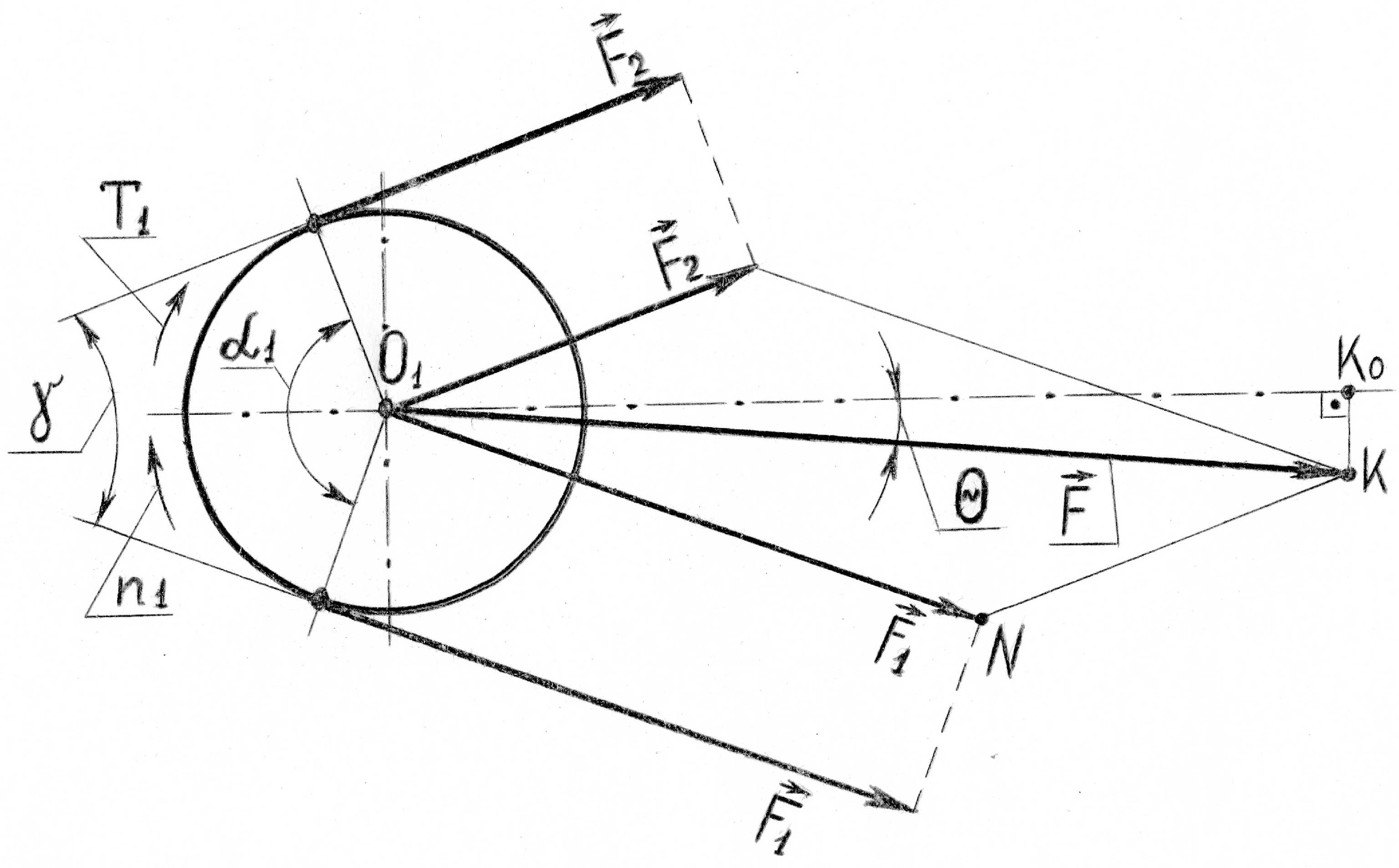
Рис. 6.1.4. Схема сил, действующих на вал

Силы в ведущей (F₁) и ведомой (F₂) ветвях ремня приведены к оси шкива, точке О₁. Результирующий вектор силы получен геометрическим суммированием векторов сил и :

Численное значение силы F находится из треугольника ΔO₁NK по теореме косинусов:

Угол отклонения Ө силы F от линии центров передачи (для рекомендуемых передаточных чисел u 6…7) достаточно мал, поэтому в инженерных расчетах им можно пренебречь. В этом случае сила F направляется по линии центров передачи, что упрощает расчет реакций в опорах.

В уточненных расчетах, где требуется учесть угол Ө, его можно определить, используя приведенную расчетную схему из ΔO₁K K_о:

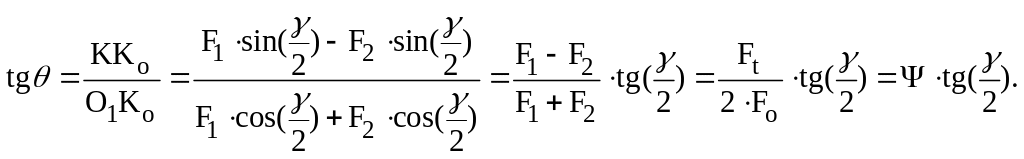
Здесь: F₁- F₂= F_t – соотношение, вытекающее из уравнения равновесия моментов от сил F₁, F₂, F_t, приведенных к оси шкива – точке О₁;

F₁₊ F₂=2 F_о – формула Ж.В.Понселе, связывающая силы в ведущей и ведомой ветвях с силой предварительного натяжения ремня F₀:

;

- коэффициент тяги, который характеризует уровень нагруженности ременной передачи.

Для клиноременных передач, работающих с нагрузкой, близкой к номинальной: Ψ≈0,45…0,55.

Расчеты показывают, что для этих значений Ψ и предельно рекомендуемых передаточных чисел u≈5…7, угол Ө не превышает 6^о.

Выбор оптимального варианта

При проектировании клиноременных передач в оболочке WinMachine, модуль APM Trans, конструктор получает большие возможности анализа, так как результаты расчетов представляют собой целый комплекс многовариантных решений (при одних и тех же исходных данных). В принципе, совокупность этих конструкторских решений можно свести к задаче многопараметрической оптимизации по одному или нескольким критериям. Теоретические основы и методика такой оптимизации хорошо разработаны, например, [1, 44], но это выходит за рамки тематики настоящего учебника. Поэтому ограничимся, общим анализом результатов машинного расчета, который лишь условно будем называть оптимизацией.

В качестве варьируемых параметров клиноременной передачи можно считать: