Порядок выполнения работы

1. Устанавливают пластинку с двойной щелью на расстоянии от лазера, включают его. Перемещая пластину с двойной щелью перпендикулярно оптической скамье, выводят интерференционные полосы на экран. Двигая пластинку с двойной щелью, добиваются того, чтобы полосы интерференции были яркими и четкими.

2. Измеряют расстояние между темными и светлыми полосами (ширину интерференционной полосы) . Для обеспечения большей точности определения необходимо измерить расстояние между удаленными, но хорошо видимыми полосами и разделить его на число световых полос .

3. Далее измеряют расстояние от пластинки с двойной щелью до экрана и по формуле (2.6) определяют . Расстояние между источниками указано на пластинке с двойной щелью.

4. Повторите опыт, изменив расстояние от пластинки с двойной щелью до экрана. Сделайте вывод, как зависит расстояние между темными и светлыми полосами от расстояния от пластинки с двойной щелью до экрана.

4. Установите вместо пластинки с известным расстоянием между щелями другую пластинку с неизвестным и по формуле (2.6) вычисляем его. Длину волны берем из предыдущего упражнения.

5. Полученные данные занесите в таблицу.

Номер опыта	t	L	ΔX	λ	Δλ

Контрольные вопросы

1. В чем заключаются особенности сложения когерентных и некогерентных волн?

2.Поясните понятие разности хода и разности фаз. Как выражается связь между ними?

3. Назовите условия усиления и ослабления света при интерференции.

4. Выведите выражение для ширины полос интерференции .

III. Дифракция света

Наблюдения свидетельствовали о нарушении прямолинейности распространения света в некоторых условиях. Так, если пропустить свет через щель, то при достаточной ее ширине края щели очерчены вполне резко. Если же щель сужать, то сначала изображение так же сужается без искажений, но затем края делаются размытыми, при дальнейшем уменьшении ширины щели ее изображение заметно расширяется. В подобных наблюдениях проявляется «загибание» световых лучей названное дифракцией.

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т.д. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает.

Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн. Огибающая этих волн задает положение волнового фронта в следующей момент времени.

Пусть плоская волна нормально падает на отверстие в непрозрачном экране. Согласно принципу Гюйгенса, каждая точка выделяемого отверстием волнового фронта служит источником вторичных волн. Построив огибающую вторичных волн для некоторого момента времени видим, что фронт волны заходит в область геометрической тени, т.е. волна, огибает края отверстия.

Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, значит световая волна, падающего на границу какого-либо непрозрачного тела, должна огибать его. Но опыт показывает, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла.

Принцип Гюйгенса решает только задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл. Дополнив его идеей интерференции вторичных волн.

Согласно принципу Гюйгенса–Френеля, световая волна, возбуждаемая каким-либо источником , может быть представлена как результат суперпозиции когерентных вторичных волн, "излучаемых" фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник . Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.

Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т.е. определить закономерности распространения света.

Немецкий физик Фраунгофер рассмотрел дифракцию плоских световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывавшего дифракцию. Чтобы осуществить такую дифракцию, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через дифракционную решетку – систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Д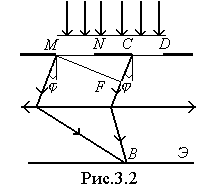 ифракционная картина на решетке является результатом взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку. На рисунке 3.2. для наглядности показаны только две соседние щели и . Если ширина каждой щели равна , а ширина непрозрачных участков между щелями , то величина называется постоянной (периодом) дифракционной решетки.

Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разность хода лучей, идущих от двух соседних щелей, будут для данного направления одинаковы в пределах всей дифракционной решетки:

(3.1)

Очевидно. что в направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. главные минимумы интенсивности будут наблюдаться в направлениях, определяемых условием:

(3.2)

Кроме того вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей , посылаемых, например, от крайних левых точек и обеих щелей. Таким образом, условие дополнительных минимумов:

.

Наоборот, действие одной щели будет усиливать действие другой, если:

(3.3)

т.е. выражение (3.3) задает условие главных максимумов дифракционной решетки.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

–главные минимумы,

–дополнительные минимумы,

–главные максимумы.

Если дифракционная решетка состоит из щелей, то условием главных минимумов является условие (3.2), условием главных максимумов–условие (3.3), а условием дополнительных минимумов:

(3.4)

где может принимать все целочисленные значения, кроме .Следовательно, в случае щелей между двумя главными максимумами располагается дополнительных минимумов.

Основными характеристиками дифракционной решетки являются ее дис­персия, разрешающая способность и область дисперсии.

Дисперсия. Угловая дисперсия определяется угловым расстоянием меж­ду двумя спектральными линиями, отличающимися на 1 нм. Если двум близ­ким спектральным линиям и , отличающимся на , соответ­ствует угловое расстояние ,то мерой угловой дисперсии яв­ляется отношение: , (3.5)

Для дифракционной решетки под , следует понимать угловое расстоя­ние в спектре одного и того же порядка между дифракционными максимумами для двух спектральных линий с отличающимися на длинами волн. Дифференцируя, получим: , откуда:

(3.6).

Как видно, угловая дисперсия возрастает с увеличением порядка спектра. Дисперсия может также определяться линейным расстоянием на эк­ране между спектральными линиями с и , отличающимися на :

(3.7).

Определенная таким образом дисперсия называется линейной, она связана с угловой дисперсией соотношением: .

Разрешающая способность. Переход от максимума данной волны к минимуму происходит более или менее плавно. Если в спектре присутствуют две близкие спектральные линии, то возможность их раздельного восприятия на данном спектральном приборе определяется не только положением их максимумов, но и тем, как быстро происходит спад интенсивностей от максимума к минимуму, или, иначе говоря, возможность разрешения спектральных линий зависит от их шири­ны.

В качестве меры разрешающей способности спектрального прибора принимается отношение длины волны, вблизи которой производится наблю­дение, к той минимальной разности длин волн ,, которая мо­жет быть разрешена на этом приборе:

.

С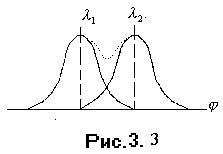 огласно критерию Релея, разрешение двух близких спектральных линий одинаковой интенсивности считается полным, когда расстояние между мак­симумами этих линий равно или больше расстояния от максимума одной из линий до ее первого минимума (рис. 3.3).

На рис. 3.3 пунктирная линия - результат сложения интенсивностей в лини­ях с длинами и / Линии в спектре видны раздельно.

В спектре порядка К положение максимума для волны длиной :

(3.8)

Условие первого минимума в том же порядке для длины волны : .

По Релею эти максимумы и минимумы видны под одним и тем же углом,

т.е.: ,

или ,

откуда: .

Положим , тогда: .

Итак, разрешающая способность дифракционной решетки определяется произведением порядка спектра на общее число ее штрихов. Чем меньше вблизи , тем более близкие линии можно будет наблюдать раздельно в ди­фракционном спектре.

Область дисперсии. В реальных условиях работы прибора мы имеем дело не с монохроматическим светом и не с набором близких моно­хроматических линий, а с некоторым спектральным интервалом конечной ширины , простирающимся от до . Благодаря этому в спектрах высоких порядков происходит наложение мак­симумов разных волн в различных порядках. Предельная ширина спек­трального интервала, при которой наложение спектров еще не происходит, называется областью дисперсии.

Для дифракционной решетки направление -го максимума для света с дли­ной волны определяется условием:

, (3.9)

максимум же порядка для волны с длиной : .(3.10)

Поскольку наложение спектров -го и -го порядков начинается при условии , то из (3.9) и (3.10) легко найти, что:

Как видим, область дисперсии сужается с увеличением порядка спектра.

ЛАБОРАТОРНАЯ РАБОТА №4

ИЗУЧЕНИЕ СПЕКТРОВ ВИДИМОГО СВЕТА С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ

Вопросы допуска

1. Какое явление называется дифракцией?

2. Как располагаются цветные линии дифракционного спектра на экране? Объясните почему?

3. По какой формуле можно определить длину световой волны с помощью дифракционной решетки? Какие величины для этого следует измерить?

Упражнение 1

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ

Цель работы: Изучение принципа работы дифракционной решетки, определение длин световых волн.

Оборудование: проекционный фонарь, дифракционная решетка, экран для наблюдения дифракционного спектра, линейка.