Порядок выполнения работы

1. Установку шкалы прибора производят по эталонному образцу с известным показателем преломления.

2. Для измерения показателя преломления той или иной жидкости: откидывают верхнюю часть измерительной головки прибора, пипеткой наносят несколько капель исследуемой жидкости на поверхность измерительной призмы, осторожно закидывают головку прибора, наблюдая в окуляр зрительной трубы и вращая маховиком измерительную головку, находят границу раздела с перекрестием нитей окуляра и снимают отсчет по шкале показателей преломления. Индексом для отсчета служит неподвижный, горизонтальный штрих шкалы. Целые, десятые, сотые и тысячные значения показателя преломления отсчитываются по шкале, десятитысячные–оцениваются на глаз.

3. Опыт провести с водой, глицерином и сахарными растворами. Полученные результаты занести в таблицу.***

№	жидкость	n

Сравнить полученные результаты со справочными данными. Сделать выводы.

4. Построить график зависимости показателя преломления сахарного раствора от концентрации сахара.

5. По графику определить неизвестную концентрацию.

Контрольные вопросы

1. Сформулировать законы отражения и преломления света.

2. Объяснить явление полного внутреннего отражения. Как используется обратное явление для измерения показателя преломления в рефрактометрах?

3. Что характеризует абсолютный показатель преломления? От каких параметров вещества может зависеть абсолютный показатель преломления?

4. Показатели преломления воды, стекла и алмаза равны соответственно 1,33, 1,5, 2,42. В каком из этих трех веществ угол преломления максимален, если угол падения во всех трех случаях одинаков?

II. Интерференция света

Рассмотрим две волны одинаковой циклической частоты , распространяющиеся в одном направлении. Накладываясь, друг на друга, они возбуждают в некоторых точках пространства колебания одинакового направления:

,

.

Амплитуда результирующего колебания в данной точке определяется, формулой: .

Если разность фаз возбуждаемых колебаний остается постоянной по времени, то волны называются когерентными, а источники таких волн – когерентными источниками. В случае некогерентных волн непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение: и .

Так как интенсивность света ~ , то интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: .

В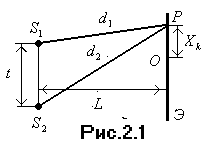 случае когерентных волн имеет постоянное во времени, но разное для каждой точки пространства значение, так что интенсивность: , (2.1) так же постоянна для каждой точки пространства.

Интенсивность света по всему полю, где происходит наложение когерентных волн, будет изменяться, причем в тех точках пространства, для которых  значения  , в тех точках, для которых  ,  . Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают устойчивые максимумы, в других минимумы интенсивности. Это явление называется интерференцией световых волн.

Особенно отчетливое проявление интерференции света наблюдается в том случае, когда интенсивность интерферирующих волн одинакова: . Согласно (2.1) в этом случае:

(2.2), в минимумах , в максимумах . Для некогерентных волн при этом же условии получается всюду одинаковая интенсивность .

Пусть и (рис. 2.1) ­– когерентные источники. Расстояние между источниками мало по сравнению с расстоянием до экрана Э, помещенного параллельно линии, соединяющей источники. Характер интерференционной картины на экране зависит от разности фаз , которую интерферирующие волны имеют в точке наблюдения . Эта разность фаз, в свою очередь, обусловлена тем, что волны от источников и до точки проходят разные пути и . Разность путей (разность хода лучей ) связана с разностью фаз , соотношением:

. (2.3)

Теперь (2.2) с учетом (2.3) можно записать в виде:

.

Интенсивность в точке будет максимальна , если выполняется условие: , или , (2.4), где – целое число.

Интенсивность в точке будет минимальна , если , или (2.5).

Условия (2.4) и (2.5) называются условиями интерференционного максимума и минимума соответственно.

В точке будет находиться центральная светлая полоса (разность хода равна 0). Расстояние от центра до -ой светлой полосы опреВеляется из условия: .

Положение темных полос определяется условием: .

Ширина интерференционной полосы или расстояние между соседними светлыми (темными) полосами ΔХ есть: , откуда . (2.6)

ЛАБОРАТОРНАЯ РАБОТА №3

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ МЕТОДОМ ЮНГА

Вопросы допуска

1. Дайте определение явлению интерференции.

2. Какие волны называются когерентными?

3. Как осуществляется интерференция в методе Юнга?

4. Как определяется длина световой волны в данной лабораторной работе?

Оборудование: оптическая скамья, лазер, экран, столик для установки пластины с двойной щелью, собирающая линза, набор стеклянных светофильтров.

Содержание и метод выполнения работы

И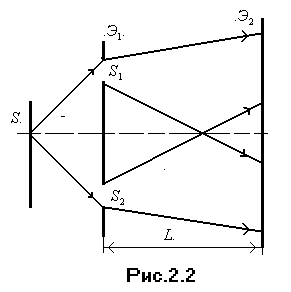 з точки S (рис.2.2) распространяется монохроматическая световая волна, которая падает на два очень малых и близко расположенных на расстоянии t друг от друга отверстия и в пластине . По принципу Гюйгенса эти два отверстия являются самостоятельными источниками световых колебаний; из этих источников будут выходить когерентные волны, т.е. происходит дифракция на узких щелях, и , параллельных , которые прорезаны в непрозрачной пластинке . За пластинкой происходит интерференция налагающихся когерентных волн, источниками которых являются щели и .

При известных расстояниях от когерентных источников и до экрана Э₂ и – между источниками по формуле (2.6) можно определить длину световой волны , измерив ширину интерференционной полосы .