Определение гидросопротивлений приточного тройника (точки к, l, b).
рис.3.3. Тройник
приточный.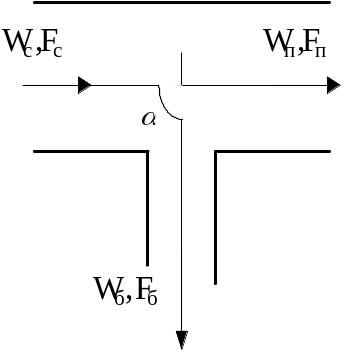
1)
При
(точки K,
L):
- коэффициент
сопротивления бокового ответвления,
приведённый к скорости в сборном рукаве
тройника;
-
коэффициент сопротивления прямого
прохода, приведённый к скорости в сборном
рукаве тройника (
не зависит от
отношения FБ/FC);
Коэффициент сопротивления бокового ответвления для приточного тройника, приведенный к средней скорости в боковом ответвлении определяется из соотношения:
Коэффициент сопротивления прохода для приточного тройника, приведенный к средней скорости в проходе определяется из соотношения:
2)
При
(точка B):
Коэффициент сопротивления бокового ответвления для приточного тройника, приведенный к средней скорости в боковом ответвлении:
;
Определение гидросопротивлений вытяжного тройника (точки m, n, e).
рис. 3.2. Тройник
вытяжной.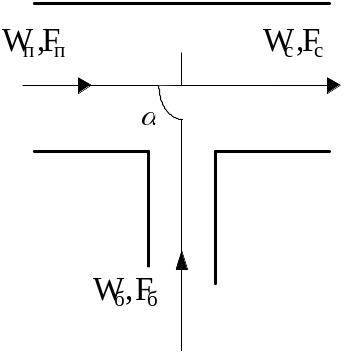
При
(точки M,
N):
;
- поправочный коэффициент;
-
коэффициент сопротивления бокового
ответвления, приведенный к скорости в
сборном рукаве;
Коэффициент
сопротивления прямого прохода
Коэффициент сопротивления бокового ответвления для вытяжного тройника, приведенный к средней скорости в боковом ответвлении определяется из соотношения:
Коэффициент сопротивления прохода для вытяжного тройника, приведенный к средней скорости в проходе определяется из соотношения:
2)
При
(точка
E):
Коэффициент сопротивления бокового ответвления, приведенный к средней скорости в боковом ответвлении:
;
Определение гидросопротивления внезапного сужения (точка c).
рис.3.4. Внезапное
сужение.
Т.к.
,
то коэффициент сопротивления внезапного
сужения определяется по формуле:
,
где
,
а
.
Коэффициент сопротивления трения:
Тогда имеем:
Определение гидросопротивления внезапного расширения (точка d).
рис.3.5. Внезапное
расширение.
Т.к.
,
то коэффициент внезапного расширения
определяют по формуле:
.
,
где
,
а
,
.
3.3.2. Расчёт характеристик Первая итерация.
Ветка №1:
рис. 3.6. Определение нивелирных высот точек L, N и j.
В етка №2:
EMBED
Equation.3
EMBED
Equation.3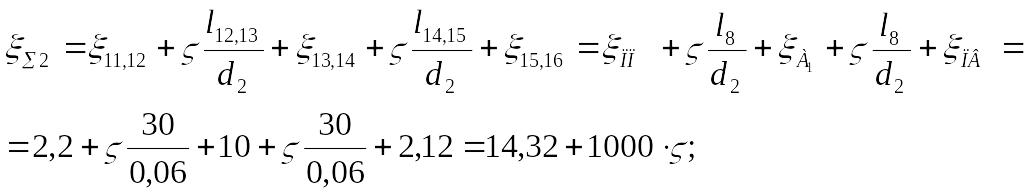
Ветка №3:
В етка №4:
Ветка №5:
Q2
В С
Ветка № 6:
Q2
D E
П
19
20 21
Ветка №7:
р
ис.
3.7. Определение нивелирных высот точек
K,
M.
K
M
Ветка №8:
Q3
K M
В етка № 9:
B K
Ветка №10:
Таблица
3.1. Результаты расчета веток с диаметром
Q |
0,0000 |
0,0035 |
0,0070 |
0,0105 |
0,0140 |
0,0175 |
0,0210 |
0,0245 |
0,0280 |
0,0315 |
0,0350 |
0,0385 |
0,0420 |
W |
0,000 |
0,198 |
0,396 |
0,594 |
0,792 |
0,990 |
1,188 |
1,386 |
1,584 |
1,783 |
1,981 |
2,179 |
2,377 |
Re*10-5 |
0,000 |
1,100 |
2,201 |
3,301 |
4,401 |
5,502 |
6,602 |
7,702 |
8,803 |
9,903 |
11,003 |
12,104 |
13,204 |
ς |
|
0,020 |
0,019 |
0,018 |
0,018 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
ξ∑5 |
|
62,543 |
57,855 |
55,992 |
54,983 |
54,348 |
53,912 |
53,594 |
53,351 |
53,160 |
53,005 |
52,878 |
52,771 |
Hпотр5 |
-13,000 |
-12,875 |
-12,537 |
-11,992 |
-11,241 |
-10,283 |
-9,120 |
-7,749 |
-6,173 |
-4,391 |
-2,402 |
-0,208 |
2,193 |
ξ∑6 |
|
62,463 |
57,775 |
55,912 |
54,903 |
54,268 |
53,832 |
53,514 |
53,271 |
53,080 |
52,925 |
52,798 |
52,691 |
Hпотр6 |
-6,000 |
-5,875 |
-5,538 |
-4,994 |
-4,244 |
-3,287 |
-2,125 |
-0,757 |
0,817 |
2,596 |
4,582 |
6,773 |
9,170 |
Таблица
3.2. Результаты расчета веток с диаметром
Q |
0,0000 |
0,0035 |
0,0070 |
0,0105 |
0,0140 |
0,0175 |
0,0210 |
0,0245 |
0,0280 |
0,0315 |
0,0350 |
0,0385 |
0,0420 |
W |
0,000 |
1,238 |
2,476 |
3,714 |
4,951 |
6,189 |
7,427 |
8,665 |
9,903 |
11,141 |
12,379 |
13,617 |
14,854 |
Re*10-5 |
0,000 |
2,751 |
5,502 |
8,252 |
11,003 |
13,754 |
16,505 |
19,256 |
22,007 |
24,757 |
27,508 |
30,259 |
33,010 |
ς |
|
0,018 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
0,017 |
ξотв |
|
0,298 |
0,296 |
0,295 |
0,295 |
0,295 |
0,295 |
0,295 |
0,294 |
0,294 |
0,294 |
0,294 |
0,294 |
ξв/р |
|
0,707 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
0,706 |
ξв/с |
|
0,475 |
0,473 |
0,473 |
0,473 |
0,472 |
0,472 |
0,472 |
0,472 |
0,472 |
0,472 |
0,472 |
0,472 |
ξ∑1 |
|
61,355 |
60,011 |
59,519 |
59,263 |
59,106 |
59,000 |
58,924 |
58,866 |
58,820 |
58,784 |
58,754 |
58,729 |
Hпотр1 |
8,500 |
13,292 |
27,248 |
50,336 |
82,556 |
123,905 |
174,385 |
233,995 |
302,735 |
380,605 |
467,605 |
563,736 |
668,996 |
ξ∑2 |
|
32,507 |
31,703 |
31,408 |
31,255 |
31,161 |
31,098 |
31,052 |
31,017 |
30,990 |
30,968 |
30,951 |
30,936 |
Hпотр2 |
8,500 |
11,039 |
18,404 |
30,577 |
47,557 |
69,342 |
95,935 |
127,333 |
163,537 |
204,548 |
250,365 |
300,987 |
356,416 |
ξ∑3 |
|
9,866 |
9,461 |
9,312 |
9,235 |
9,188 |
9,156 |
9,133 |
9,115 |
9,102 |
9,091 |
9,082 |
9,074 |
Hпотр3 |
4,250 |
5,021 |
7,206 |
10,796 |
15,790 |
22,189 |
29,992 |
39,200 |
49,812 |
61,827 |
75,248 |
90,072 |
106,301 |
ξ∑4 |
|
10,098 |
9,694 |
9,546 |
9,469 |
9,422 |
9,390 |
9,367 |
9,350 |
9,336 |
9,325 |
9,316 |
9,309 |
Hпотр4 |
4,250 |
5,039 |
7,278 |
10,960 |
16,083 |
22,646 |
30,651 |
40,096 |
50,983 |
63,310 |
77,079 |
92,288 |
108,938 |
ξ∑7 |
|
61,355 |
60,011 |
59,519 |
59,263 |
59,106 |
59,000 |
58,924 |
58,866 |
58,820 |
58,784 |
58,754 |
58,729 |
Hпотр7 |
-1,000 |
3,792 |
17,748 |
40,836 |
73,056 |
114,405 |
164,885 |
224,495 |
293,235 |
371,105 |
458,105 |
554,236 |
659,496 |
ξ∑8 |
|
32,507 |
31,703 |
31,408 |
31,255 |
31,161 |
31,098 |
31,052 |
31,017 |
30,990 |
30,968 |
30,951 |
30,936 |
Hпотр8 |
-1,000 |
1,539 |
8,904 |
21,077 |
38,057 |
59,842 |
86,435 |
117,833 |
154,037 |
195,048 |
240,865 |
291,487 |
346,916 |
ξ∑9 |
|
9,667 |
9,265 |
9,118 |
9,041 |
8,994 |
8,962 |
8,939 |
8,922 |
8,909 |
8,898 |
8,889 |
8,881 |
Hпотр9 |
-0,500 |
0,255 |
2,394 |
5,909 |
10,798 |
17,061 |
24,698 |
33,710 |
44,096 |
55,856 |
68,991 |
83,499 |
99,382 |
ξ∑10 |
|
10,553 |
10,151 |
10,004 |
9,928 |
9,881 |
9,849 |
9,826 |
9,809 |
9,795 |
9,784 |
9,775 |
9,768 |
Hпотр10 |
-0,500 |
0,324 |
2,671 |
6,532 |
11,906 |
18,792 |
27,191 |
37,103 |
48,528 |
61,465 |
75,915 |
91,878 |
109,353 |