1.1.11 Основы математической статистики. Оценка математического ожидания, дисперсии, коэффициента корреляции.

Математическая статистика — наука о математических методах систематизации и использования статистических данных для научных и практических выводов.

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании).

Математическая статистика — раздел математики, посвященный методам анализа данных, преимущественно вероятностной природы. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы.

Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез.

Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т.д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики опираются на продвинутую теорию и возможности современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости.

Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр.

Вероятностное пространство — это тройка , где

— это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;

— сигма-алгебра подмножеств , называемых (случайными) событиями;

— вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

Элементарные события (элементы ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.

Каждое случайное событие (элемент ) — это подмножество . Говорят, что в результате эксперимента произошло случайное событие , если (элементарный) исход эксперимента является элементом .

Требование, что является сигма-алгеброй подмножеств , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.

Математическое ожидание — понятие среднего значения случайной величины в теории вероятностей. Обозначается через , в статистике часто используют обозначение .

Пусть задано вероятностное пространство и определённая на нём случайная величина . То есть, по определению, — измеримая функция. Тогда, если существует интеграл Лебега от по пространству , то он называется математическим ожиданием, или средним значением и обозначается :

.

Если — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега-Стилтьеса:

.

Простейшие свойства математического ожидания

• Математическое ожидание линейно, то есть

, где — случайные величины с конечным математическим ожиданием, а — произвольные константы;

• Математическое ожидание сохраняет неравенства, то есть если почти наверное, — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины также конечно, и более того ;

• Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если почти наверное, то ;

• Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий .

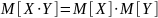Дисперсия случайной величины — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается . Квадратный корень из дисперсии, равный , называетсясреднеквадратичным отклонением, станда́ртным отклоне́нием или стандартным разбросом.

Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда:

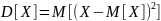
Свойства:

• Дисперсия любой случайной величины неотрицательна;

• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

• Если случайная величина равна константе, то её дисперсия равна нулю. Верно и обратное: если почти всюду;

• Дисперсия суммы двух случайных величин равна: , где - их ковариация;

• Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

• В частности, 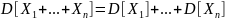для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

• ;

• ;

• .

Ковариация в теории вероятностей — это мера линейной зависимости двух случайных величин.

Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.

Коэффициент корреляции в теории вероятностей и статистике — это показатель характера взаимного стохастического влияния изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой в математической статистике и может принимать значения . Если значение по модулю находится ближе к , то это означает наличие сильной связи, а если ближе к — связь слабая или вообще отсутствует. При коэффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть изменения двух величин можно описать математической функцией.

Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:

Пусть — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

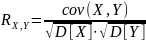,где 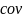— ковариация, — дисперсия.

Развернутый вариант формулы:

, где — математическое ожидание.